时间序列分析在股票收益率中的应用——基于ARIMA和ARCH模型

(云南财经大学 云南 昆明 650221)

一、背景及研究现状

中国的股票市场历经十几年的发展逐渐成熟，成为我国最重要的资本市场之一。对于中国股市的管理者来说，如何把握股市的动态，使其健康、稳定的发展，也是一项艰巨的任务。所以无论是投资者还是管理者都对股票市场特别关注，尤其对股票市场分析以及未来行情的预测，更是成为一个热门研究的课题。

近来年金融时间序列这个领域越来越受到人们的关注，尤其是当2003年时，RobertEngle和CliveGranger两位教授获得了诺贝尔经济学奖之后。随着计算机的快速发展，针对具有明显趋势项的非平稳时间序列，Box和Jenkins于1976年，提出自回归求和移动平均模型——ARIMA模型[1]。1982年Engle(1982)在分析英国通货膨胀率序列时，针对方差是非齐次提出了自回归条件异方差模型——ARCH模型。近些年也有国内很多学者对金融时间序列分析进行进一步的研究(张波等，2017；杨文宁等，2017)，使这一方法得以发展并产生广泛的应用。但是时间序列分析在对原始非平稳数据的处理、预测精度的提高以及针对具体数据如何选择合适的时间序列模型或如何构建组合模型方面有待进一步的研究。

二、理论模型

(一)ARMA模型

ARMA模型全称是自回归移动平均模型，它是目前最常用的拟合平稳序列的模型。可以细分为AR模型，MA模型和ARMA模型三大类[1]。

ARMA(p,q)模型的形式为：

(3.1)

若φ0=0，该模型称为中心化ARMA(p,q)模型。ARMA模型在时间序列分析中十分普遍而且十分典型，其中AR模型和MA模型是它两个特殊的情况。

(二)ARIMA模型

对数据进行差分，得到平稳序列的性质，这时我们称这个非平稳序列为差分平稳序列，可以用ARIMA模型进行拟合。

ARIMA(p,d,q)模型的形式为：

(3.2)

三、数据选取与实证分析

数据来源于Inter公司股票从1973年1月到2002年12月的月收益率。数据从http://faculty.chicagobooth.edu/ruey.tsay/teaching/bs41202/sp2017/网址上下载。

(一)拟合ARMA模型

通过对原序列进行序列的纯随机性检验，得出p值大于显著性水平，因此该序列不能拒绝纯随机的原假设。随后，我们对序列进行了一阶差分然后再进行纯随机检验，这时可以得到结论如表4.1

表4.1 Box-Piercetest检验

一阶差分后，p值远远小于显著性水平，因此拒绝原假设，即拒绝序列是纯随机的。做出ACF和PACF的图，如图4.1

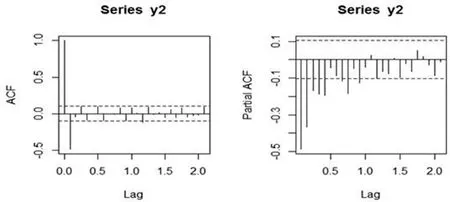
图4.2 ACF和PACF检验

由ACF和PACF看出来，序列均是拖尾的。我们对序列进行ARIMA拟合，采用ARIMA(5,1,4)模型，模型见公式4.1，同时进行残差白噪声检验，检验结果见表4.2

xt=0.36xt-1-0.9xt-2+0.11xt-3+0.01xt-4+0.04xt-5+εt-1.32εt-1+0.61εt-2-1.23εt-3-0.95εt-4

(4.1)

表4.2

各延迟下LB统计量P值都显著大于0.05，可以认为这个拟合模型的残差序列属于白噪声序列，该拟合模型显著有效。接下来，我们对拟合的模型进行预测，预测12个月的股票收益率，拟合结果如下

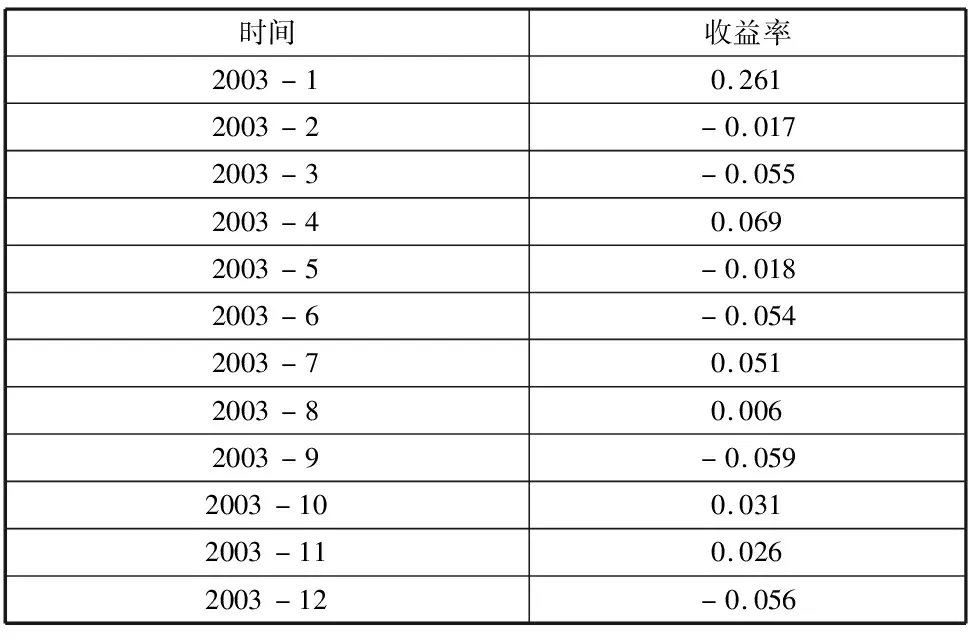
表4.3 拟合收益率

从预测结果上来说，预测结果较好。

(二)拟合ARCH和GRACH模型

对于金融时间序列，我们通常采用条件异方差模型。从时序图来看，在1973年1月往后第20个月前后，90个月前后，125个月前后以及170个月前后，序列波动很大，呈现集群效应。

对数据进行拉格朗日乘子检验(LM)，得到

表4.4 ARCH-LM检验结果

从表4.4中可以得出，这个数据具有ARCH效应。对于金融时间序列，我们通常采取的数据处理方法是取对数。我们多这个数据取对数，研究对数收益率。

进行拟合ARCH(1)模型，结果如下

(4.2)

通过进行检验，检验结果如表4.5所示

表4.5 ARCH检验结果

可以看出，拟合的效果不是很好，p值不是很大，接下来拟合GARCH(1,1)模型，拟合结果如下：

(4.3)

表4.6 GARCH检验结果

可以看出GARCH(1,1)模型要比ARCH(1)模型好一些。接下来对GARCH(1,1)模型进行预测，预测后12个月，预测结果如下

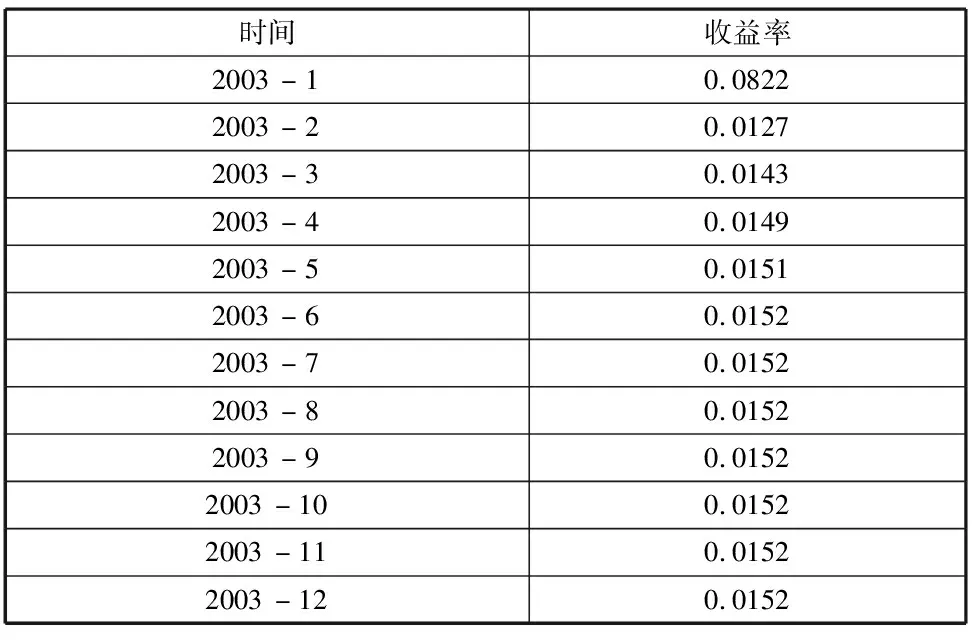
表4.7 GARCH预测结果

根据结果可以看出GARCH(1,1)模型预测效果并没有ARIMA(5,1,4)模型效果好。

四、结论

本文采用Inter公司股票的月收益率作为数据，应用了ARIMA模型、ARCH模型和GARCH模型对股票收益率进行了研究。根据分析结果看出股票的收益率存在异方差性，采取条件异方差模型是比较好的处理方法。但格局股票预测的结果，发现ARIMA模型却要比GARCH模型拟合效果更好一些。