用导数法求解距离问题的策略

白进忠

导数是高中数学的重要内容,是研究和解决数学问题的重要工具,它为我们解决曲线与曲线之间距离的最值问题提供了便利.本文从探究一道高考题出发,总结求解这类题型的通法.

图1

通常解题时都离不开距离的“垂直性”和“最近性”,而“最近性”就是求距离的最小值，平面上点与直线(曲线)、直线与直线(曲线)、曲线与曲线的距离问题通常都是求距离的最小值,这是高考的常考题型.

1 可转化为点到直线的距离问题

1.1 求曲线上一点到直线的最短距离

图2

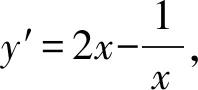
1.2 求曲线上一点到另一条曲线上一点的最短距离

图3

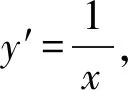
2 可转化为两点间的距离问题

2.1 求直线与曲线的水平距离问题

图4

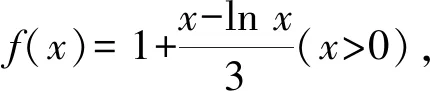
2.2 求直线与曲线的铅垂线距离问题

图5

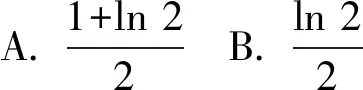
|MN|=|y1-y2|=
|a2-lna|=a2-lna(a>0).

3 可转化为直线与曲线间距离问题

①

c-d-2=0,

②

图6

在①中，设b=y,a=x,则y=x3-2lnx(x>0),在②中，设d=y,c=x,则y=x-2,易知(a-c)2+(b-d)2表示曲线y=x3-2lnx与直线y=x-2上两点之间的最小距离的平方,图象如图6.

总之,曲线与曲线之间的距离问题,利用化归转化和数形结合的思想可把问题转化为点到直线的距离、两点间的距离问题,再利用导数法来求距离的最值.解题目标清楚,解题思路清晰,图象直观,方法简单明了,有利于促进学生解题能力的提升.