装配式宽桥预拱度影响因素及合理线型研究

■刘 洋

(贵州省交通规划勘察设计研究院股份有限公司，贵阳 550081)

0 前言

预拱度的合理设置是桥梁线型平顺、行车流畅、桥梁正常使用的可靠保证[1]。虽然国内外学者对预拱度开展了较多的研究[2-5]，但对装配式预应力混凝土宽梁桥的预拱度影响因素的研究仍比较少见。 本文依托某三跨30m 装配式先简支后连续小箱梁， 针对预拱度的影响因素进行敏感性分析，并给出了更为精准的预拱度线型模型，以期为今后类似桥梁的设计和施工提供参考。

1 预拱度影响因素敏感性分析

1.1 结构刚度

结构刚度是表征桥梁整体变形能力的重要指标，其大小主要受材料特性、结构截面尺寸等影响，而弹性模量能够较为直观地反映其材料特性的变化。 考虑到在役超静定混凝土结构自身裂化及与环境耦合等耐久性作用，截面弹性模量和挠度必然发生时效性变化， 因而弹性模量能有效评估结构挠度的的变化。

通过采取降低结构弹性模量的方式来模拟结构整体刚度的变化， 依次考虑混凝土弹性模量折减5%、10%、15%、20%、25%，其余参数不变时对主梁线形的影响。

由图1 可知，结构刚度折减5%时，边跨边梁最大挠度增加0.89mm，相比于原挠度值(17.15mm)增加5%，边跨中梁最大挠度增加0.90mm，相对于原挠度值(17.43mm)增加5%。 结构刚度折减25%时， 边跨边梁最大挠度增加5.72mm，相对于原挠度值(17.15mm)增加33%；边跨中梁最大挠度增加5.81mm，相对于原挠度值(17.43mm)增加33%。 随着结构刚度的线性折减，挠度值呈现线性增加趋势，且结构刚度变化引起的挠度增量效应显著。

考虑到桥梁运营过程中混凝土劣化、 钢筋锈蚀等病害导致的结构刚度衰减，结构下挠效应显著，因此在设计阶段计算预拱度时应考虑结构刚度的影响。

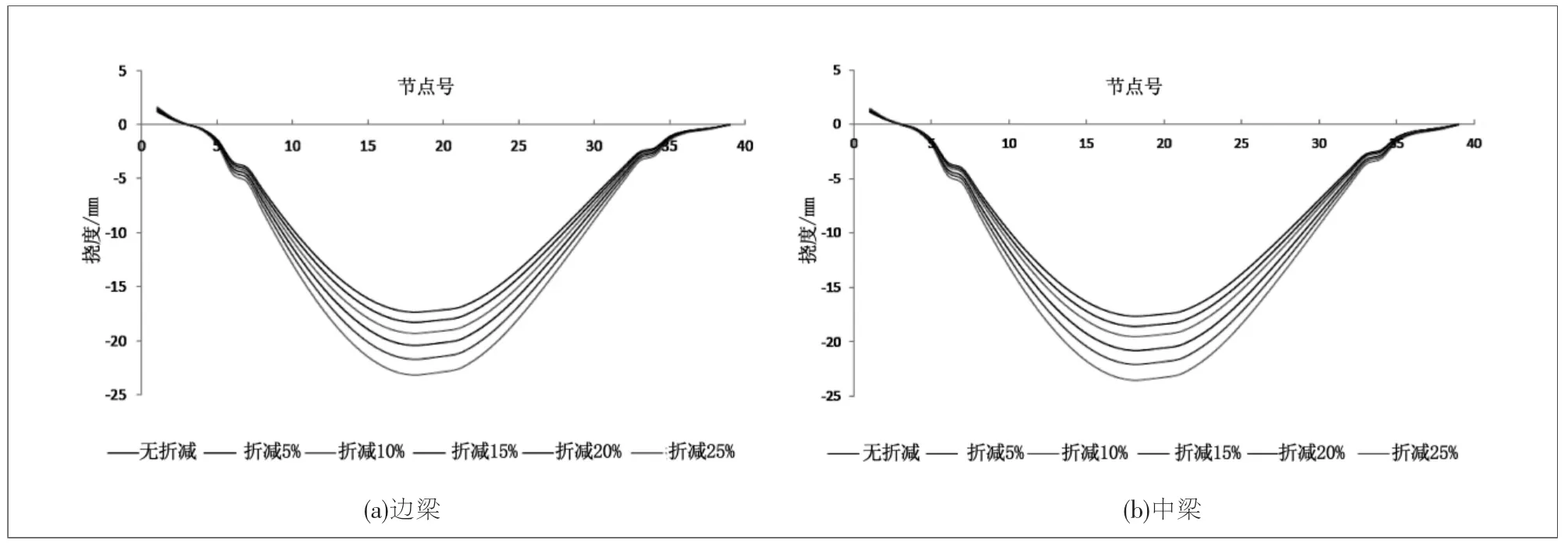
图1 结构刚度影响下边跨挠度变化图

1.2 预应力损失

预应力能够较好地抑制主梁的应力水平和挠度，纵向预应力损失会致使桥梁挠度产生较大增幅[6]。由于施工及运营期间的钢束松弛和混凝土收缩徐变等客观原因，势必会导致纵向预应力损失逐渐增大， 其对混凝土梁体的约束作用降低， 进而导致连续桥梁的跨中挠度发生变化。

图2 给出了预应力影响下边跨挠度的响应规律。 预应力损失增大10%时， 边跨边梁最大挠度相较于预应力未发生折减时增大了1.46mm，相对于原挠度值(17.15mm)增大了9%，边跨中梁最大挠度相较于预应力未发生折减时增大了1.47mm，相对于原挠度值(17.43mm)增大了8%。预应力损失增大30%时， 边跨边梁最大挠度相较于预应力未发生折减时增大了4.71mm， 相对于原挠度值(17.15mm)增大了27%，边跨中梁最大挠度相较于预应力未发生折减时增大了4.08mm，相对于原挠度值(17.43mm)增大了23%；

随着预应力钢筋的预应力损失增大， 边跨的下挠基本上呈线性增大，预拱度对预应力损失比较敏感，对结构变形影响显著。预应力束受施工工法、材料特性和环境条件等影响，长时间服役下会产生较大损失，甚至无法满足设计的反拱值， 因此在设计阶段计算预拱度时要充分考虑预应力损失的影响。

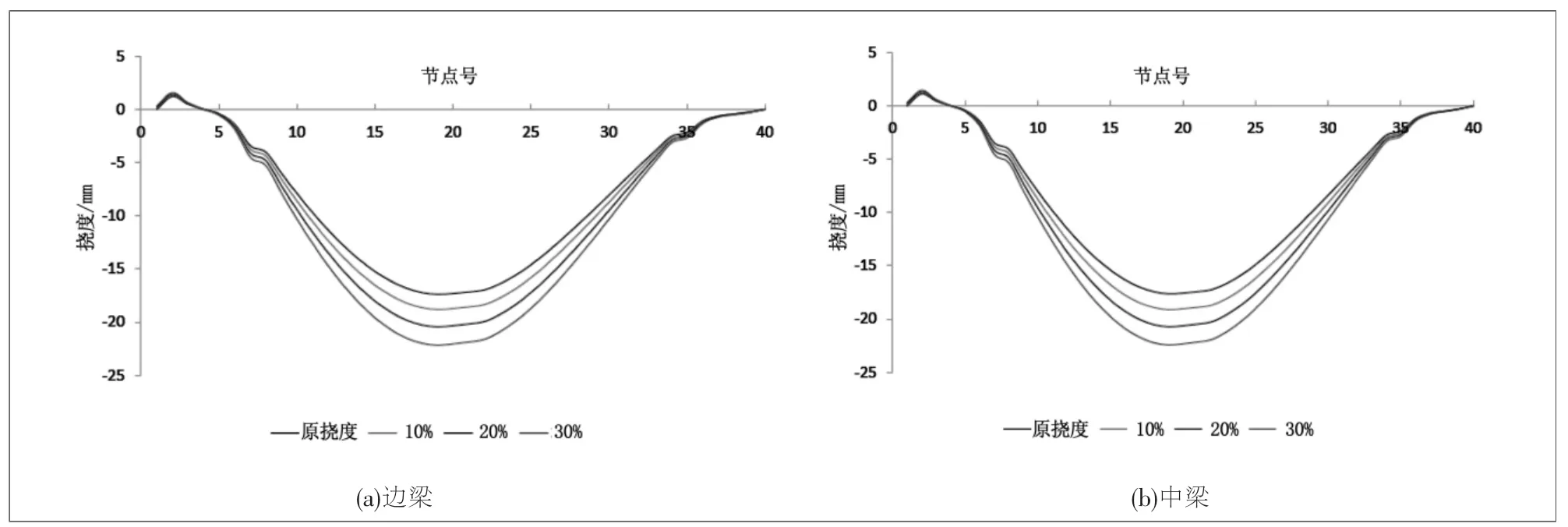
图2 预应力影响下边跨挠度变化图

1.3 收缩徐变

作为混凝土的固有特性和重要力学性能， 混凝土收缩徐变受到约束后会使结构应力及内力发生重分布，在长时间内引起结构的变形[7]。

考虑到徐变增加速率随时间递减， 大部分徐变在两年内就完成，5 至20 年后徐变增长达极限值。 现分别给出宽桥成桥阶段、运营1 年、运营2 年、运营3 年、运营5年和运营10 年的挠度值。

由图3 可知，运营1 年时，边跨边梁最大挠度相较于刚成桥增大了0.88mm，相对于原挠度值(16.15mm)增大了5.4%， 边跨中梁最大挠度相较于刚成桥增大了0.89mm，相对于原挠度值(16.42mm)增大了5.4%；运营两年时，边跨边最大挠度相较于刚成桥增大了0.91mm，相对于原挠度值(16.42mm)增大了5.6%，边跨中梁最大挠度相较于刚成桥增大了0.92mm，相对于原挠度值(16.42mm)增大了5.6%，；运营十年时，边跨边梁最大挠度相较于刚成桥增大了1.0mm，相对于原挠度值(16.42mm)增大了6.2%，边跨中梁最大挠度相较于刚成桥增大了1.01mm，相对于原挠度值(16.42mm)增大了6.1%。

图3 收缩徐变影响下边跨中梁挠度变化图

随着混凝土收缩徐变的发生， 边跨的跨中挠度均呈现为首年变化较大，运营一年后挠度基本保持不变，最终边跨跨中挠度增大6%左右。运营一年时收缩徐变对挠度的影响已基本定型，挠度变化趋稳。

1.4 宽跨比

研究宽跨比对装配式宽桥预拱度的影响， 主要考虑结构自重、二期恒载、预应力和收缩徐变等四个方面的因素保持不变，通过改变宽跨比，计算不同宽跨比情况下的挠度， 故考虑宽跨比为0.75、1、1.25、1.5 和2 的情况下的挠度，来研究宽跨比对挠度的影响。

观察图4 可知，30m 跨径的三跨连续小箱梁桥，随着宽跨比的变化挠度基本不变， 在两个边跨最大挠度达到了17mm。 因此施工时，应根据桥梁规范结合施工现场的存梁期、砼配合比、材料特性及地区气候等，综合考虑计算边、中跨的纵向反拱度。

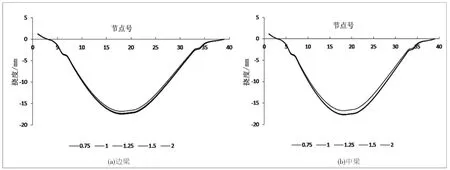
图4 宽跨比影响下边跨中梁挠度变化图

2 预拱度的合理线型

2.1 边跨线形理论假设

为了探究多跨连续梁桥的变形曲线形式， 特别是边跨线形的复杂性。 根据梁桥的实际变形与受力情况对计算模型进行如下简化：

(1)连续梁受到的作用等效为均布荷载作用于梁上；

(2)边跨端简化为具有初始θ 的固定端(如图5 所示)。θ 可以较好地反映支座的类型，固定支座时，θ=0；活动支座时，按实际合理取值。

图5 多跨连续梁桥边跨的受力简化图

取任意x 位置处截面， 则计算得其挠曲线平衡微分方程如下：

其中,l 为边跨跨径；E 为弹性模量； I 为截面惯性矩；Ra为a 端支座反力；q 为均布荷载集度。

进而得挠曲线方程：

由边界条件

将(2)代入(3)中解得：

将(4)代入(2)中得挠曲线方程：

公式(5)表明，连续梁边跨挠曲变形属于四次多项式曲线范畴， 即施工中常采用的2 次抛物线并不能精准揭示多跨连续梁边跨的预拱度线形。

2.2 预拱度线型的拟合

鉴于篇幅限制， 本文结合前文有限元的计算数值直接给出预拱度线形拟合结果，如表1 及图6 所示。

表1 函数拟合结果汇总表

图6 函数拟合结果对比曲线图

观察表2 可知， 规范中推荐的二次函数的拟合度略差，用高斯函数拟合的结果要比二次函数更优，与前两者相比起来四次多项式的拟合度要更高一些， 而拟合度最佳的是三角函数拟合的结果， 这同时也验证了前述理论线型的可靠性。

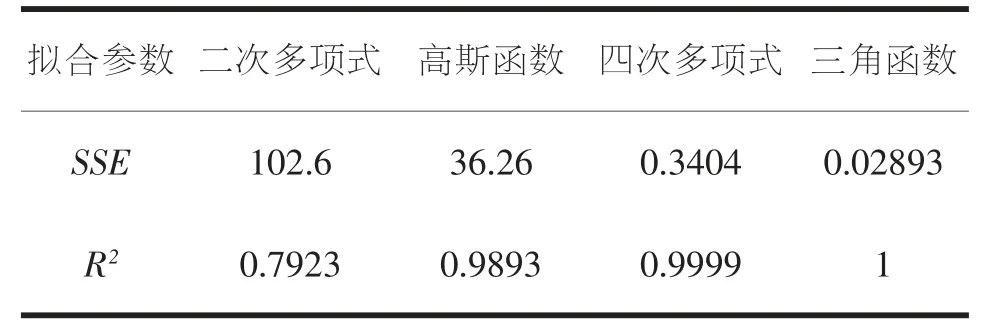
表2 函数的拟合程度对比

3 结语

(1)装配式宽桥的预拱度影响因素中结构刚度降低、预应力损失、收缩徐变三个因素对预拱度的影响较大，宽跨比变化对预拱度的影响较小。

(2)装配式宽桥纵向预拱度研究结果表明，连续梁边跨预拱度采用四次多项式描述更为精准， 可为今后连续梁桥的预拱度线形设计提供新的借鉴思路。 但值得注意的是， 目前实际施工中， 边跨预拱度普遍采用二次抛物线， 这主要是考虑到施工的便捷性及工程实际精度亦可满足要求。