带电粒子在正交叠加场中运动问题的研究

胡连冬

(湖南省长沙市宁乡县第七高级中学 410635)

本文中的“正交叠加场”是指同一空间中同时存在两种或两种以上相互垂直的匀强场，并且其中之一是匀强磁场.当带电粒子在叠加场中运动时，由于叠加场中存在匀强磁场，粒子受到的合力大小方向不断变化，导致粒子在叠加场中做变加速曲线运动；这类问题涉及知识的综合性强，难度系数大，解题能力的要求较高.针对此类问题如何化难为易，成为高三物理复习教学中教师普遍关注的问题.

一、两种基本方法的论证

1.证明动量定理能确定粒子在匀强磁场中运动的位移

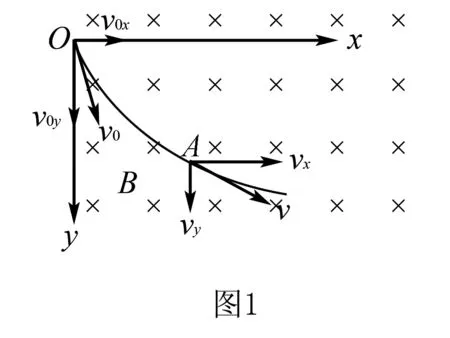
在某一区域内有磁感应强度为B，方向垂直纸面向里的匀强磁场，一带电量为+q，质量为m的粒子从O点以初速度V0垂直射入磁场中，当粒子运动到A点时，其速度方向如图1所示(不计重力)，试分析粒子从O运动到A的时间内，粒子沿X,Y轴方向发生的位移x,y跟粒子速度的关系？

析与证粒子在A点所受洛仑兹力沿X,Y轴方向上的分力为：

fx=BqVyfy=-BqVx

由动量定理得：BqVyΔt=mΔVx

根据微元法：y=∑VyΔt∑mΔVx=mVx-mV0x

x=∑VxΔt∑mΔVy=mVy-mV0y

则：Bqy=mVx-mV0x①

Bqx=-(mVy-mV0y) ②

①②两式成立的条件是：粒子在X,Y轴方向上只受洛仑兹力，或除洛仑兹力外其他力的合力等于零.

上面①②两式即为洛仑兹力在X,Y轴上的分力的冲量，跟粒子沿X,Y轴方向上动量的变化关系(动量定理)，其中x、y表示粒子沿x轴和y轴方向上发生的位移；V0x、V0y、Vx、Vy表示粒子沿x轴y轴方向的初末速度.

2.证明用速度分解法能确定粒子在匀强磁场中运动的轨迹

在中学物理问题中，通常复杂的曲线运动可以等效为简单的直线运动或简单的曲线运动进行研究.

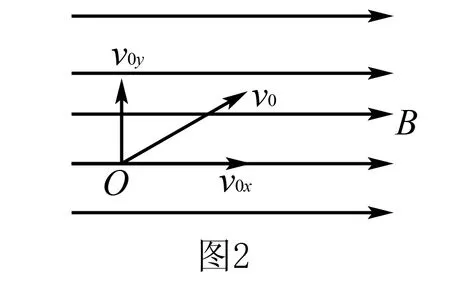
如图2所示，在空间存在水平向右的匀强磁场，磁感应强度为B，一带电量为+q，质量为m的粒子从O点以初速度V0与磁感应强度成θ角方向射入磁场，不计粒子的重力，判断粒子在磁场中做什么运动？

析与证将初速度V0分解为水平分速V0X=V0cosθ和竖直分速V0y=V0sinθ.由于V0x平行B，故粒子在V0x方向不受力而以V0x速度做匀速直线运动，V0y垂直于B，粒子受洛仑兹力f=BqV0y作用在垂直B的竖直平面内做顺时针方向的匀速圆周运动.即粒子的运动是由沿Vox方向上的匀速运动和垂直B平面内的匀速圆周运动组成.

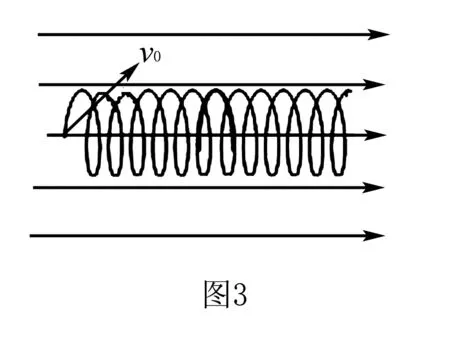
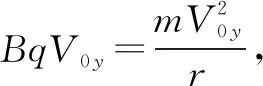
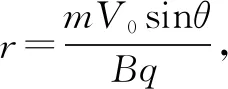
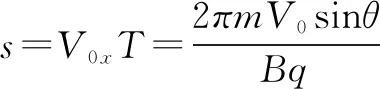
粒子运动轨迹是螺旋线，如图3所示.

二、方法运用

对于带电粒子在叠加场中运动问题，只要善于运用动量定理和速度分解法，就能将复杂的问题转化为学生熟悉的模型，最终突破解题“瓶颈”.

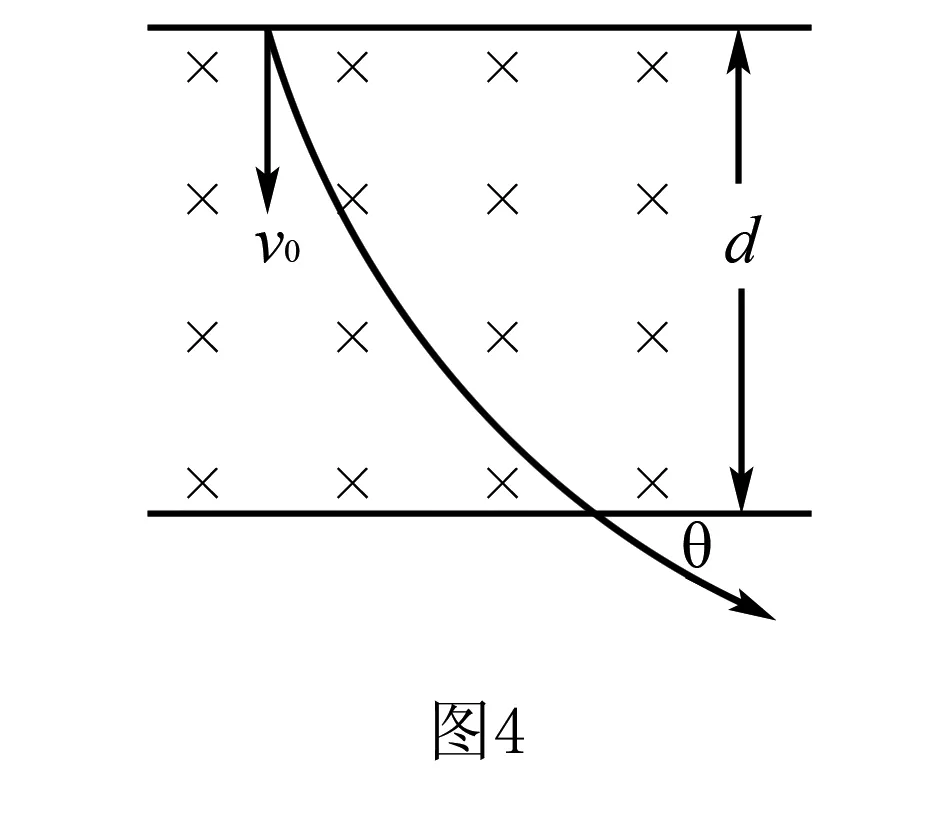
例1如图4所示，一质量为m、带电量为q的带电粒子(重力不能忽略)，以速度V0从上方竖直进入一宽度为d的匀强磁场区域中，磁感应强度为B，试求粒子飞出磁场时与水平方向的夹角θ.

析与解由于粒子在水平方向只受洛仑兹力的分力作用，由动量定理的：Bqd=mVcosθ③

由于洛仑兹力不做功，根据动能定理有：

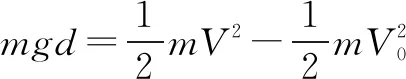
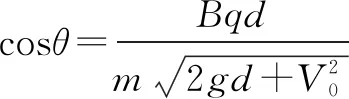
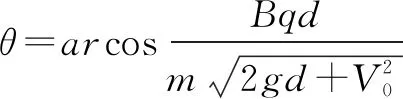
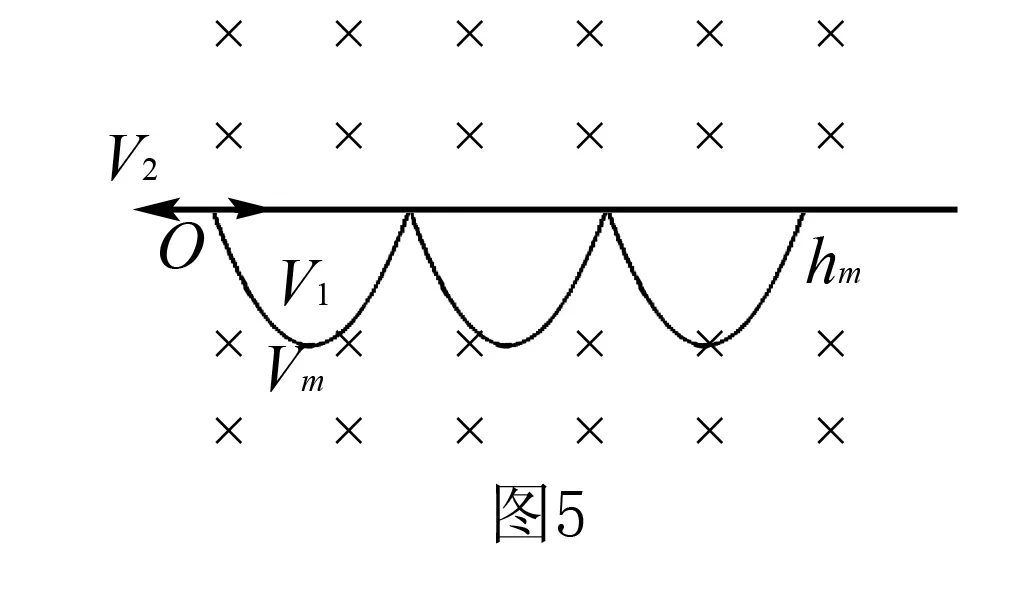
例2空间存在垂直纸面向里的匀强磁场，磁感应强度为B，质量为m，带电量为+q的微粒在磁场中由静止释放(重力不能忽略)，分析粒子做什么运动？

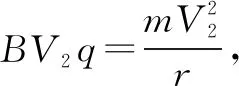
上述两例解析分别运用了动量能量的观点和速度分解法，前者以粒子运动的过程分析为依托，从动量和能量相结合的角度分析问题；后者以粒子的初始条件和初始条件下粒子的受力情况分析为契机，分解粒子的初速度，从合运动与分运动等效的角度解决问题.

三、解题策略

1.已知粒子的运动情况，求其运动状态，优先动量和能量相结合的观点解题

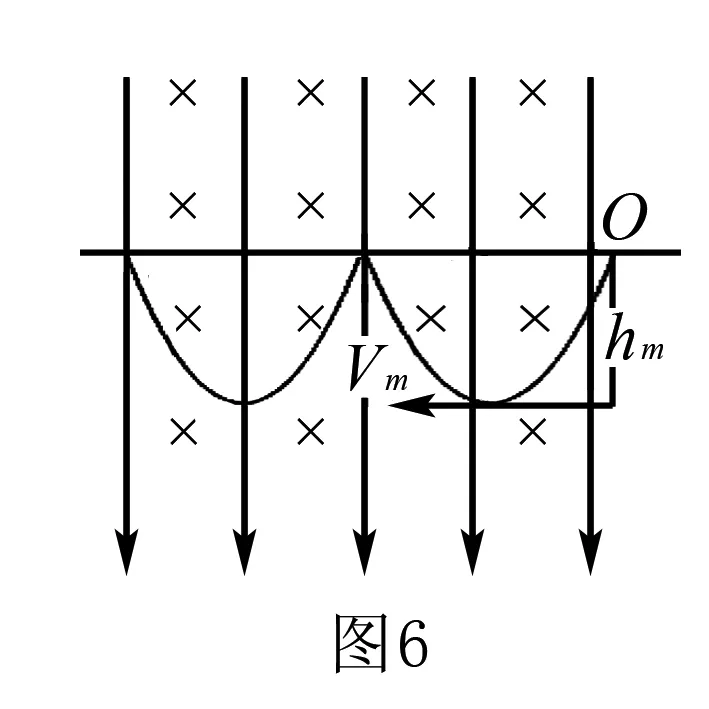
例3如图6所示，空间存在着正交的匀强电场和匀强磁场，电场方向竖直向下，电场强度为E，磁场方向水平且垂直纸面向里，磁感应强度为B，在这叠加场中的O点，有一带负电的油滴，其质量为m，电量为-q，将油滴由静止释放，不计空气阻力，求油滴运动过程中下落的最大高度和最大速度(设mg>Eq)

析与解根据条件mg>Eq,可知油滴运动到最低位置时速度最大.若油滴运动到最低位置时下降的高度为hm，具有的速度为Vm.由动量定理得：qBhm=mVm⑤

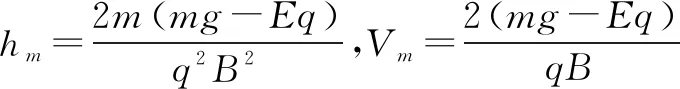
运用动量能量的观点研究问题时，必须根据带电粒子在场中的受力情况及各场力的做功情况，判断粒子的运动状态具有什么特征(粒子是否具有最大或最小速度，何时运动到最高或最低位置等)，把握洛仑兹力的冲量跟粒子动量的变化关系，列出动量定理和动能定理的表达式，然后解方程组.

2.已知粒子的初始状态，求其运动情况，优先速度分解法解题

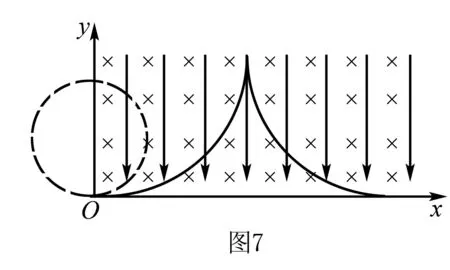
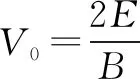
(1)此带电粒子到达的地方到X轴的最远距离；

(2)粒子运动轨迹跟X轴相切的点的坐标(不计重力)

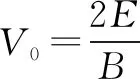
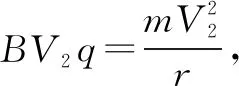
故粒子与X轴相切点的坐标是：

速度分解法是从粒子运动的初始条件入手，分析粒子初始状态及受力情况，对粒子的初速度合理分解，使某一方向的洛仑兹力跟电场力或重力(或电场力和重力的合力)平衡，从而将粒子复杂的运动转化为简单的匀速直线运动和匀速圆周运动.

带电粒子在叠加场中运动问题，在近几年高考和自主招生考试以及物理竞赛中常成为命题的热点之一.针对这类问题，教师应当以问题探究为载体，运用变式教学法，渗透学生已具备的物理学思想方法，为学生搭建思维平台，降低问题难度；在教学实践中，教师要指导学生学会运用“动量、能量的观点及速度分解的观点”去研究问题；使学生面对变化多端的问题时，能以变应变，以不变应万变.