例谈向量数量积问题的处理策略

王兆龙

(上海市建平中学 200135)

一、代数化

代数化包括数量积的定义和坐标表示．

1．利用定义

当两向量a、b的模、夹角都比较容易求出时，直接利用定义a·b=|a||b|cosθ计算数量积，其中θ是向量a、b的夹角．

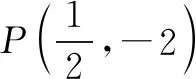
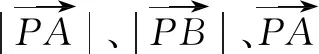
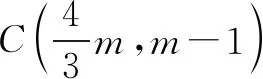
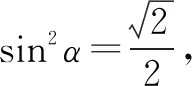
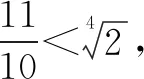
2．利用坐标表示

用坐标运算代替向量运算，用代数方法解决几何问题．

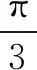
分析a、b都与e有关，给定e之后可得a、b的终点轨迹，再借助几何图形求解．

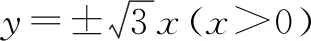
二、几何化

几何化包括数量积的几何意义、向量垂直的数量积表示和极化恒等式．

1．利用数量积的几何意义

数量积a·b的几何意义是向量b的模与a在b方向上投影的乘积．特别地，如果b是一个固定的向量，只要求出a在b方向上投影(或范围)，即可求出a·b的值(或范围)．

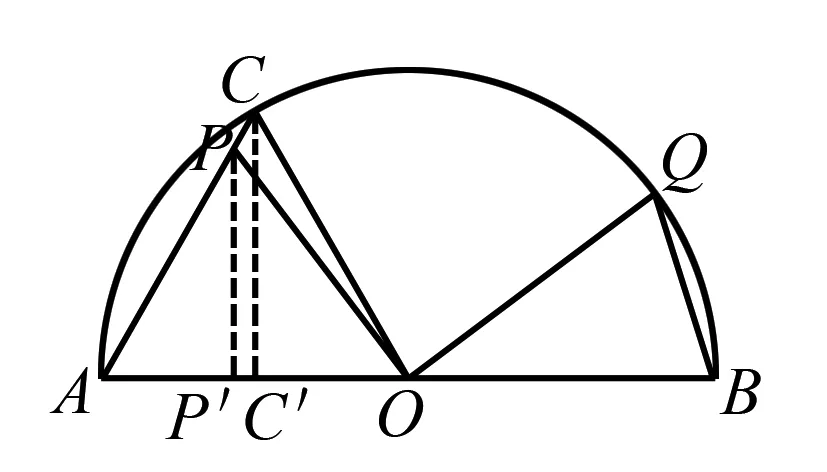
图2

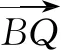
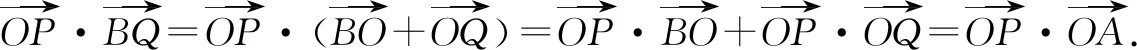
2．利用向量垂直的数量积表示

若两个共起点(终点)向量的数量积为0，则这两个向量垂直，且起点(终点)在以两个终点(起点)连线段为直径的圆上，可将代数问题转化为几何问题求解．

例4 (2015上海虹口二模)已知向量a、b满足|a|=|b|=a·b=2，若向量c满足(a-c)·(b-c)=0，求|2b-c|的最小值．

分析将a、b、c起点重合，利用(a-c)·(b-c)=0研究c的终点轨迹．

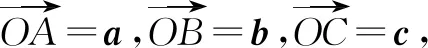
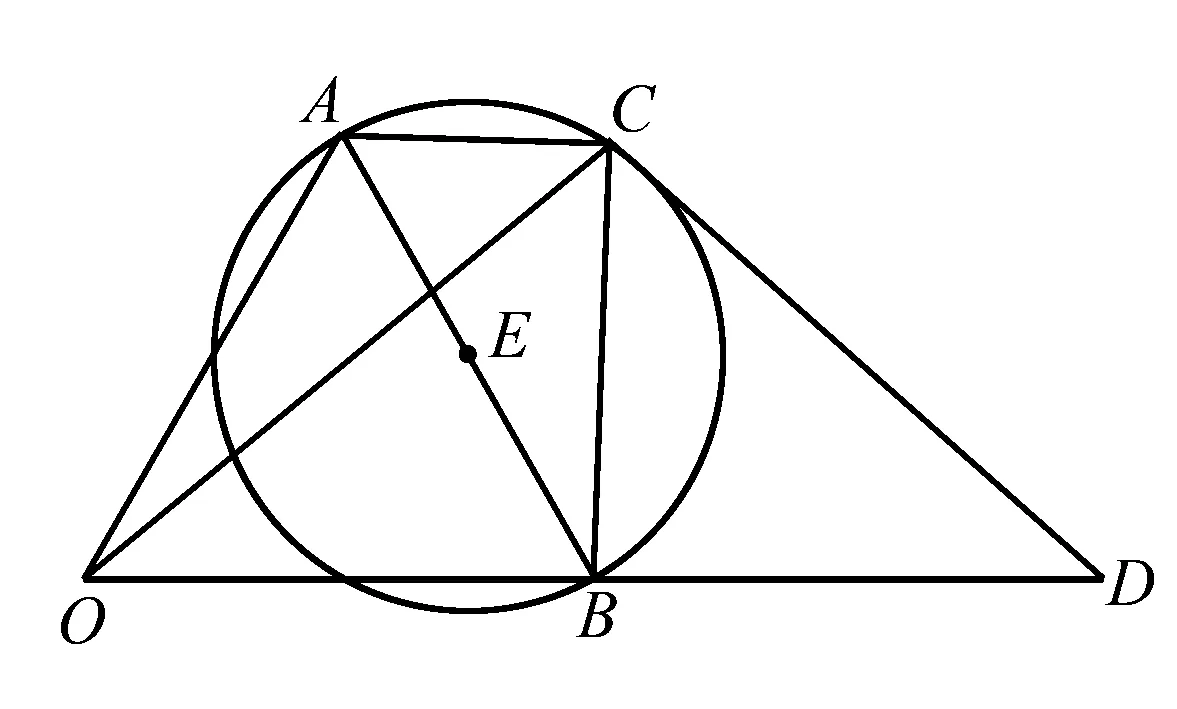
图3

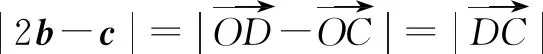
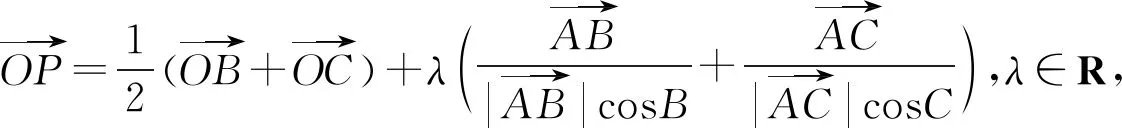
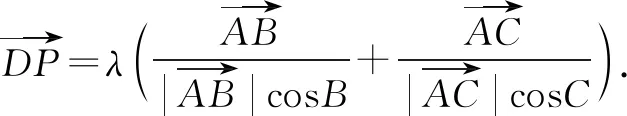
解设边BC的中点为D，则

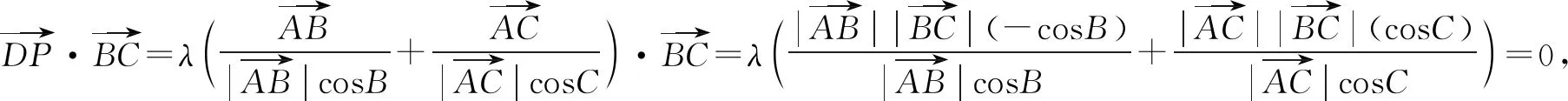
3．利用极化恒等式

三角形中的极化恒等式是借助三角形的边和中线将数量积转化为线段长的一组等式，在处理一边或中线为定长的求数量积的最值问题中可以大量地简化运算．

设D是△ABC边BC的中点，则

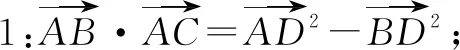
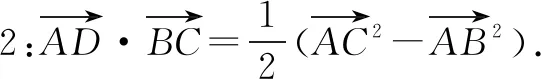
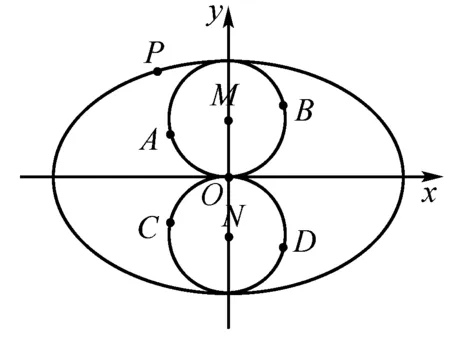
图4

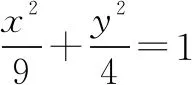
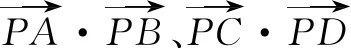
解由极化恒等式1，

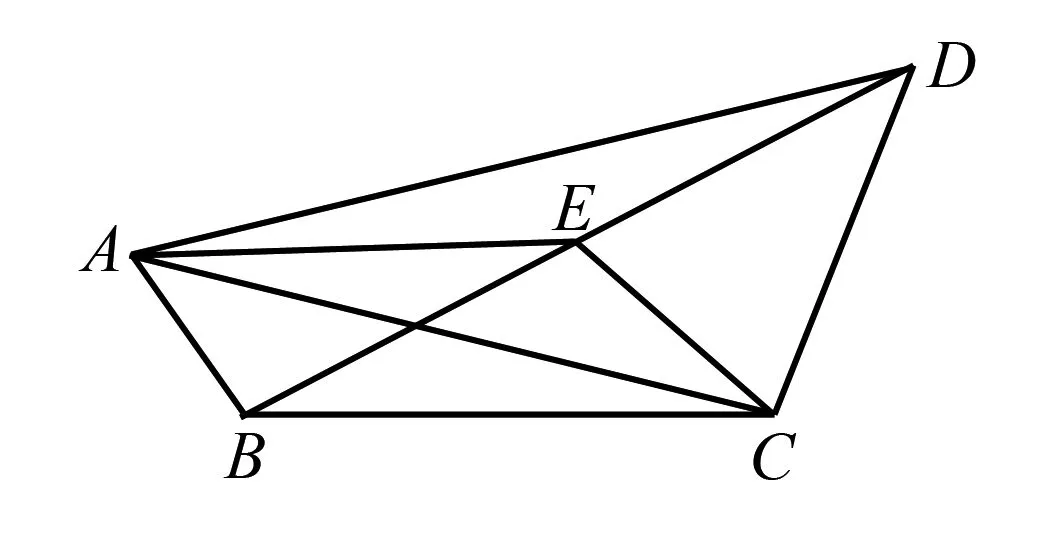
图5

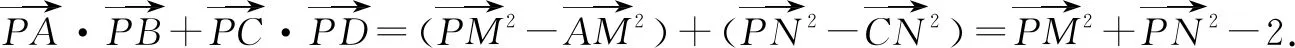
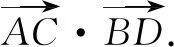
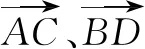
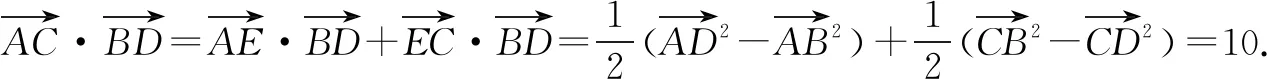
三、基底化

基底化是指将所求向量用一组基向量表示，用基向量的运算代替所求向量的运算．基向量的选取应以尽可能多地知道向量的相关条件(模、夹角)为原则．

利用平面向量分解定理

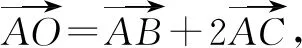
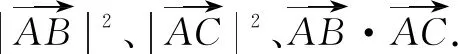
解注意到