三角形面积的最值及取值范围的解法初探

陈 娟

(福建省福州第十一中学 350001)

解三角形是高考数学的必考知识点，主要考查的问题有解三角形、三角形面积的计算及求三角形中的相关量的最值和取值范围.对于大部分学生而言，“求三角形中的相关量的最值和取值范围”这类问题是个难点，下面我们以近几年高考中对三角形面积的最值或者取值范围的考查为例，探讨如何解决此类问题.

此类的问题中的三角形都不是唯一确定的，所以主要有以下两种类型.

一、已知三角形的一边及其对角

例1(2014年全国卷Ⅰ理16)已知a,b,c分别为△ABC三个内角A，B，C的对边，a=2，且(2+b)(sinA-sinB)=(c-b)sinC，则△ABC面积的最大值为____.

解法由a=2,可知

(a+b)(sinA-sinB)=(c-b)sinC，

又根据正弦定理，得(a+b)(a-b)=(c-b)c，

化简得，b2+c2-a2=bc.

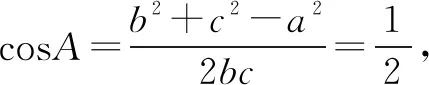
解法2 由正弦定理得：

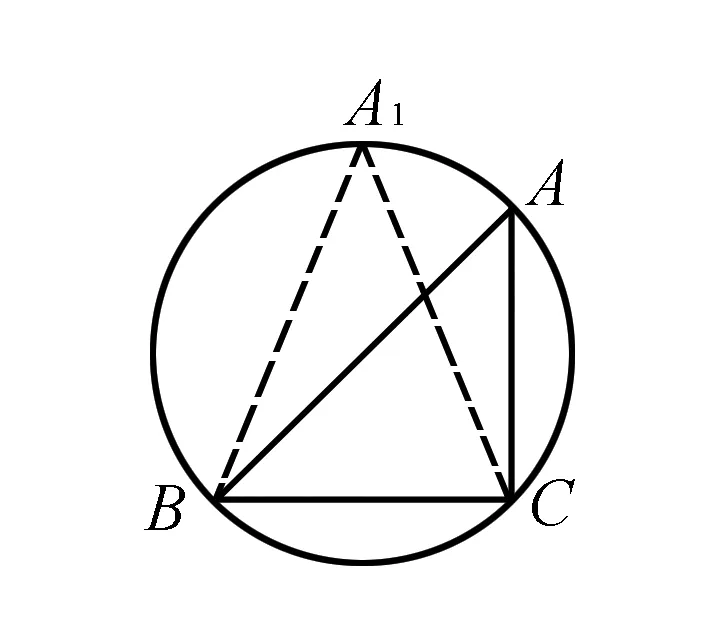
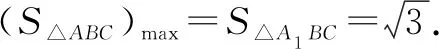
从本题的题目架设出发，采用解法1的余弦定理结合基本不等式来解决是非常自然的，用解法2的正弦定理构造三角函数显得有点刻意，但是作为填空题，还是更多的考虑从“对边对角”这个几何特征出发，用解法3来解决.

二、已知三角形的一边及一角(非对角)

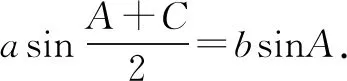
(1)求B；

(2)若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.

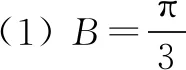
解法1 由正弦定理得：

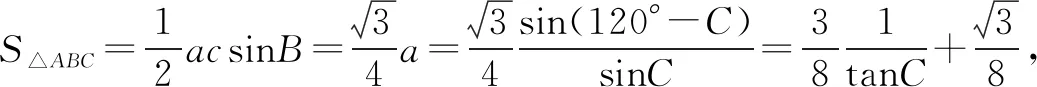
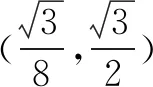
本题求的是取值范围，相对于题1，利用正弦定理构造出三角函数来求解是非常顺畅且自然而然的.此外，能否利用已知的边角特征，用几何法来解决呢？这也是可以的.

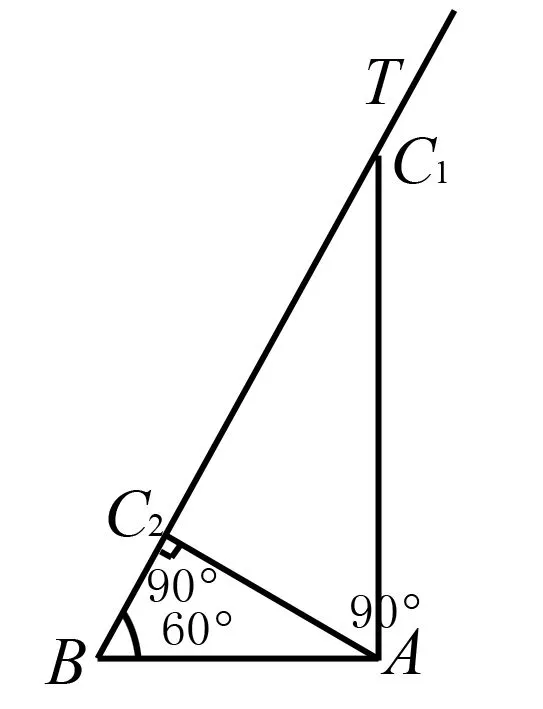
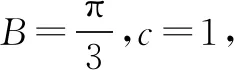
从上面的两道高考题可知，我们解决三角形面积的最值或者取值范围的问题，主要有两种方法，一是抓住这类问题的代数本质，结合正弦定理及余弦定理，用基本不等式或者构造函数的方法来解决；二是找到这类问题的几何本质，抓住它们的几何特征，在选填题中可以小题小做，达到事半功倍的效果.