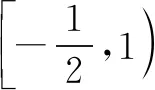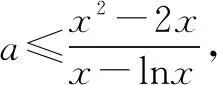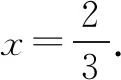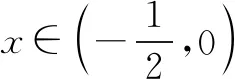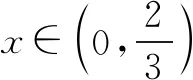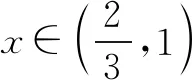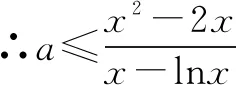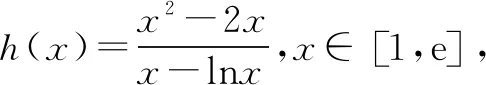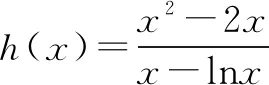探究导数与函数极值、最值的实际运用
黄惠强
(湖北省黄冈中学惠州学校 438000)
利用导数求函数极值和最值是函数解题过程中的一种常见方法,但同样该种方法还可以运用到其他方面,从而有效地加深学生对极值和最值的理解.因此,本文将结合实际解题经验,从利用导数与极值求函数的最值、利用导数与极值求参数的范围、利用导数与最值研究恒成立问题三个方面入手,探究利用导数求极值和最值的实际运用.
一、利用导数与极值求函数的最值
求函数的最值问题是高考常见的题型,涉及到的知识面较广,方法灵活多样.我们可以利用函数的有界性和单调性等性质来进行解答,只要运用得当,就可以有效地简化整个题目的难度,使得学生快速找到解题的方法.下面将以函数的单调性为切入点,探讨如何利用导数与极值来求函数的最值.
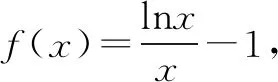
思考在本题中函数只可能在区间的端点或者在极值点取得最大值.而本题解题的关键是极值点的位置,所以第一步就要对极值点是否在[m,2m]内进行讨论,再有效的借助函数的单调性,就可以得到函数的最值.
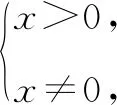
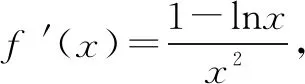
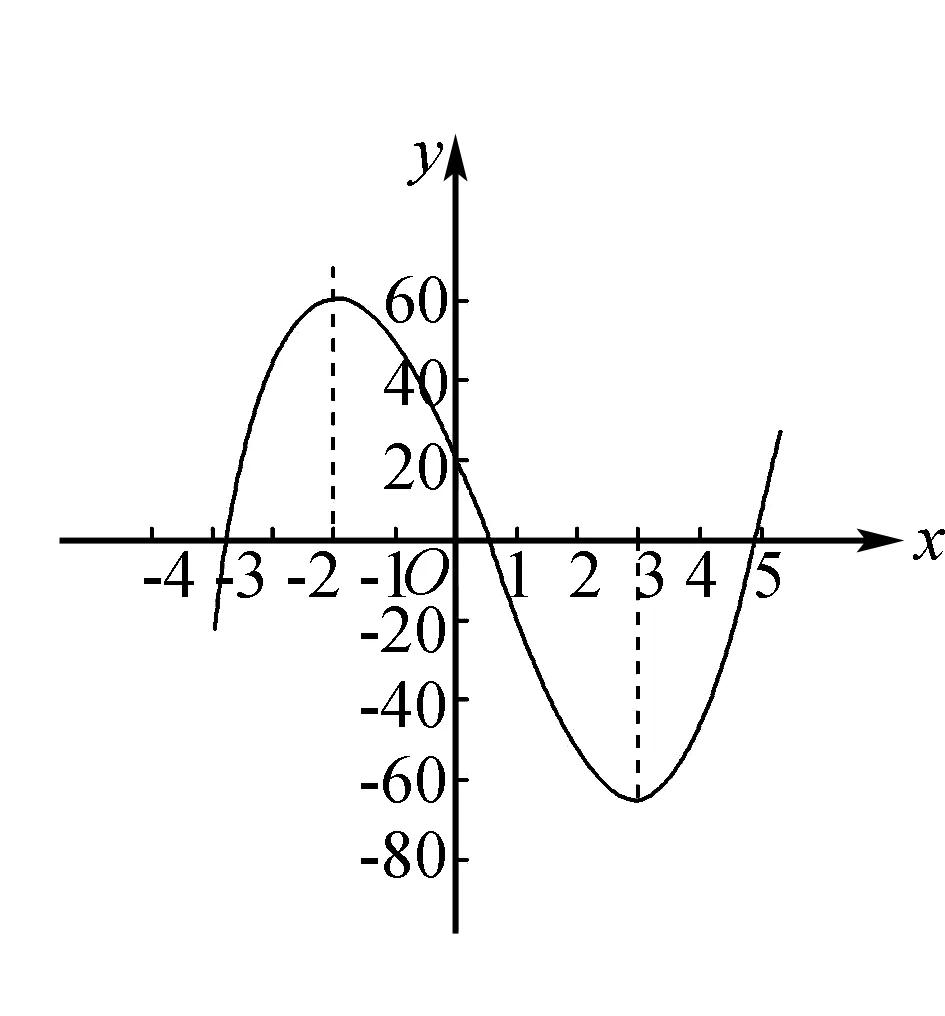
由f′(x)>0,得0 由f′(x)<0,得x>e. ∴f(x)在区间(0,e)上单调递增,在区间(e,+∞)上单调递减. (3)当e≤m时,函数f(x)在区间[m,2m]上单调递减, 注意:通过观察是看不出本题中函数的单调性,故要对函数进行求导,接着求出函数的极值和单调区间,再结合函数的大致图象就能快速找到突破口,从而有效地解题.但在运用此种方法时,必须着重确认函数的定义域.在大部分函数中,定义域存在一定的限定条件,给解题增添了一定的难度,所以在解函数类题目时要养成“不求定义域不做题”的习惯. 利用导数与极值求参数的范围问题在高考题目中相对较难,由于引入了未知的参数,学生很容易考虑不全面,从而导致答题不完整,得不到完整的分数.因此,在利用极值求参数的范围时,首先要将题目中的参数采取一定的方式从原式分离出来,然后再利用其不含参数一边的式子求出函数的单调区间和极值再进行求解,就能有效地找到参数所能够满足的范围区间. 例2已知函数f(x)=2x3-3x2-36x+16-a(a为实数),若方程f(x)=0有三个不同实根,求实数a的取值范围. 思考这是一个明显地利用函数单调性和极值求参数范围的问题.方程f(x)=0即2x3-3x2-36x+16-a=0.在解答过程中先分离参数,可得到2x3-3x2-36x+16=a.方程f(x)=0有三个不同实根可转化为函数y=a与y=2x3-3x2-36x+16的图象有3个交点的问题. 解析方程f(x)=0即2x3-3x2-36x+16-a=0. 则2x3-3x2-36x+16=a. 令g(x)=2x3-3x2-36x+16, 则g′(x)=6x2-6x-36=6(x-3)(x+2). 由g′(x)>0得x<-2或x>3; 由g′(x)<0得-2 ∴函数g(x)的递增区间是(-∞,-2)和(3,+∞),递减区间是(-2,3) 由已知得g(-2)=60,g(3)=-65,g(0)=16. 图1 ∴结合函数单调性及以上关键点画出函数g(x)的大致图象如图所示. 方程f(x)=0有三个不同实根即函数y=a与g(x)=2x3-3x2-36x+16的图象有3个交点, ∴a∈(-65,60) 注意:本题的解题关键是求出函数的导数和极值,然后有效地利用函数的单调性和关键点画出函数的大致图象,最后通过观察函数的图象求出参数a的范围.在实际解题过程中,需要注意极值点并不一定是函数的最值点,而是函数值增大与减小的临界点. 恒成立问题一直是高考命题的热点,把不等式恒成立问题、函数问题和导数问题交汇命制压轴题成为一个新的热点命题方向.在解答这类问题的过程中,教师可以引导学生尝试利用函数的最值来进降低试题的难度.从本质上来看,就是有效地利用了转化这一思想,将恒成立问题转化为求最值的问题,使得整个题目的突破口更加明显,从而有效解题. 例3已知函数f(x)=-x3+x2+b,g(x)=alnx. (2)若对任意的x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围. 解析(1)f′(x)=-3x2+2x=-x(3x-2). ∴b=0. (2)由g(x)≥-x2+(a+2)x, 得(x-lnx)a≤x2-2x. ∵x∈[1,e], ∴lnx≤1≤x,由于不能同时取等号, ∴lnx 当x∈[1,e]时,x-1≥0,x+2-2lnx=x+2(1-lnx)>0,从而h′(x)≥0. ∴h(x)min=h(1)=-1, ∴a≤-1. 故实数a的取值范围为(-∞,-1]. 注意:利用最值可以研究某一类恒成立的问题.一般来说,f(x)≥a对x∈R恒成立等价于f(x)min≥a;f(x)≤a对x∈R恒成立等价于f(x)max≤a. 总之,在函数解题的实际过程中,适当地利用导数可以有效的简化问题.因此,教师要引导学生利用导数研究函数的极值和最值,再将它们与其他题型融合,就能解答很大一部分与函数相关的题目,从而提升学生的数学水平,让学生取得更好的成绩.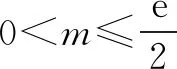
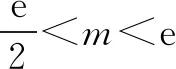
二、利用导数与极值求参数的范围
三、利用导数与最值研究恒成立问题