中职生逻辑思维能力的培养及途径
苏淑莲
(顺德胡锦超职业技术学校,广东 佛山 528305)
逻辑思维能力不仅对学习有好处,而且是处理日常生活问题的一种能力。数学中的逻辑思维能力是指根据正确思维规律和思维形式对数学对象的属性进行比较、分析综合、抽象概括、归纳、推理论证的能力。正确思维形式是指明确地使用概念,恰当地下判断,合乎逻辑地进行推理。概念、定理是推理的出发点,概念不明确,就不能进行推理。下面举例说明:
例1:a为什么实数时:(a2-4)x2-2(a+1)x+1=0有实根?
“有实根”与“有两个实根”“有两个不同的实根”是不同的概念,部分学生将这三个概念混为一谈、不明确,因而出现这样的结果:
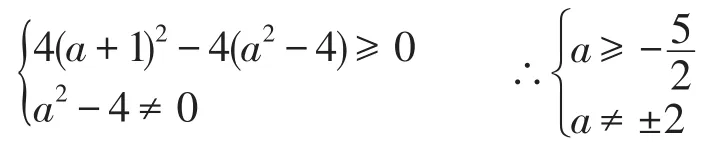
另一部分学生会这样列式:
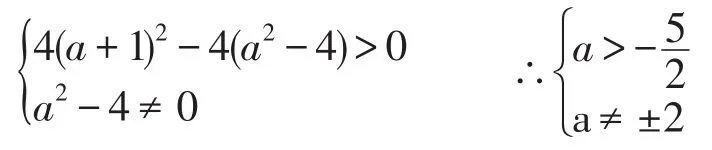
1 培养逻辑思维能力的重要性
在社会转型和改革的新时期,要大力发展教育事业的今天,只有学生的逻辑思维得到发展,他们掌握数学基础知识就更容易,他们才能掌握解决实际问题的本领。作为数学,有高度的抽象性、严密的逻辑性和应用的广泛性。作为数学教学过程,必须培养学生逻辑思维能力。对于中职生,他们已经开始学习专业知识,很快要走向自己的工作岗位,有很多的生活问题亟待解决。培养逻辑思维能力显得更为重要,这个年龄的学生思维正在明显地向严密化、抽象化、概括化发展,在逻辑思维上可塑性大,在数学教学中,加强训练,使学生的逻辑思维能力获得良好的发展。有的教师认为,培养学生的运算能力主要在代数教学中进行,而平面几何的主要任务是培养学生的逻辑思维能力。事实上,只要认识培养学生逻辑思维能力的重要性,在代数、三角、解析几何中都有大量的问题。
例2:在ABC中,最大角A是最小角C的二倍,且三边长为三个连续整数,求证:三边之长为4、5、6。要讲述问题,在概念方面要知道怎么表示是“三个连续整数”?“最大角”与“最小角”,在抽象与概括能力方面,这三角形三边如何用抽象的字母表示?用x,x+1,x+2表示呢?还是用x-1,x,x+1表示三角形的三边?在培养学生的分析能力与综合能力方面,可提出最大角与最小角之间有什么关系?如何用“在一个三角形中,大边(x+1表示的边)对大角(C表示)”画出一个草图来?在推理与论证方面,如何以正弦定理与余弦定理组成一个联系已知量与未知量的方程?为什么又要以正弦定理与余弦定理作为论据呢?这些启发性问题都是根据培养学生逻辑思维能力的原则而设计、提出来的。

2 培养逻辑思维能力的途径
严格遵守逻辑规律,正确运用逻辑思维形式,做出示范,潜移默化是培养学生逻辑思维能力的宽广的途径。数学教学中的作图、证明、运算都蕴含着逻辑推理的因素。在传授知识时,计算题要讲清的转化过程:讲定理、公式时,要讲清规律的发生过程与推导过程。作图是要讲清分析过程以显露图像特征。比如函数y=| sinx|的周期。如何在讲解中培养学生的逻辑思维能力呢?由于中职生的年龄特征,正是由直观的形象思维向着抽象的逻辑思维转化,教师首先应该用直观发现的创造性思维来引导学生求y=|sinx|的周期。事实上,y=sinx的图像在-π到0这一段是在X轴下方。根据绝对值的性质,在此区间内,y=|sinx|的函数图像应该与y=sinx的图像关于X轴成轴对称图形,而是0到π这一段,y=|sinx|与y=sinx的图像是相同的,在其他区间上类似地研究。于是,学生可以直观发现y=|sinx|的周期是π。其次,从周期函数的定义出发,存在一个常数π,使得当取定义域内的每一个值时,都有|sin(x+π)|=|-sinx|=|sinx|成立,那么y=|sinx|是π以为周期的周期函数。
我们想进行严格的逻辑推理,运用已有的知识、方法、技巧与解题经验,运用转化的思想,也可推出的周期也是π。
这样,求y=|sinx|的周期转化成求的周期
故|sinx|的周期等于。三种方法,由直观图像的直觉思维到抽象思维,求出了y=|sinx|的同一个周期。要培养学生的逻辑思维能力,为了求出复杂函数的周期,必须使学生直观地观察函数图像,不能画出图像的题,必须将异名函数化成同名函数的形式,用三角公式sin2x+cos2x=1,1-2sin2x=cos2x,使异名函数转化成同名函数。只有这样,学生知其然,又知其所以然。久而久之,学生才能以逻辑思维能力去独立地获取知识。数学中的证明更蕴含着逻辑推理过程。在论证过程中,也要给学生做出示范,以培养学生的逻辑思维能力。笔者在进行推理论证的过程中,提高了学生的抽象概括能力、推理证明的能力。为了培养学生的逻辑思维能力,还必须加强充要条件的数学。到了职中阶段,将有关知识抽象概括成一些规律性,让学生去类比联想,以发现新的规律。这也是培养学生逻辑思维的手段之一,加强数学推理证明的训练,是提高学生的逻辑思维能力更有效的途径。人的逻辑思维是从具体形象思维到抽象思维,逻辑思维会帮助人更好地采集、收集和储存以及交换信息。培养逻辑思维能够帮助人在未来社会生存环境中能够主动地编织“目的性逻辑思维”,能主动积极地为目的的实现而进行信息交换。逻辑思维能力帮助人们提高智力和创造力,养成一定社会价值的综合能力。

