浅谈连接体的关联加速度问题

余建刚

一、问题的由来

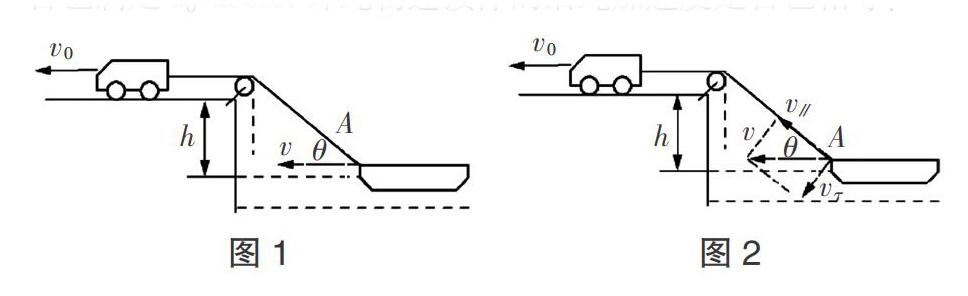
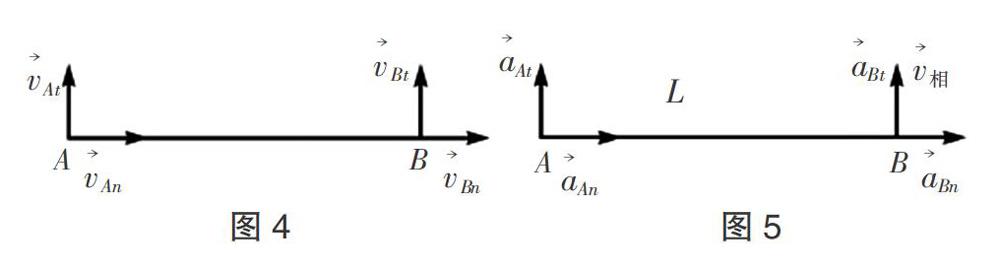
在高中的习题中，常会见到如下题目：“如图1所示，在离水面高度为h的岸边，有人用小车通过绳子拉船靠岸，若车的速度恒为v0，试求：当绳子与竖直方向的夹角为？兹时，船的速度为多少？”

此题较为简单，由于绳子不可伸长，沿绳各点速率相等，如图2，我们可将船速正交分解为沿绳和垂直于绳;车的速率v0等于船沿绳分速度vn. 即v0=vn=vcos？茲. 既然绳物连接体的沿绳速度相等，那么，倘若小车的加速度为a0，则船的加速度是否也满足a0=acos？兹. 即绳物连接体的沿绳加速度是否也相等？

不少学生想当然地以为，既然速度沿绳速度相同，则它们沿绳加速度也一定相同，并列出“充分的物理依据”：“根据a=，由于绳子不可伸长，则沿绳各点速率相等，又绳子上各点经历时间相等，所以沿绳各点的加速度也必然相等，故有a0=acos？兹 ”. 持这一错误的观点的学生不在少数，当前有不少老师对这一的解答比较笼统，不能给学生一个信服的解释，以致学生一知不解，不知所以然. 卢瑟福有一句名言：“只有当你能把一个理论讲得连女仆都能听懂，你才算真懂了.”为了给学生一个清晰透彻、有说服力的解答，于是笔者撰写此文，以达抛砖引玉之效.

二、问题的分析

我们首先来看看学生所认为的沿绳加速度相同，其求解小船所谓的“充分的物理依据”，中出现了概念错误，加速度的定义应是对速度的求导，学生的解法的前提必须是绳与船前进方向间夹角保持不变才可能正确. 但实际上船在前进过程中绳子与船前进方向间夹角会发生变化. 下面列出二种解法.