强化自我反思——谈“矛盾冲突”对初中数学课堂教学的影响

马 龙

（甘肃省陇南市成县城关中学，甘肃陇南 742500）

引 言

数学知识具有独特的魅力，此种魅力可以通过矛盾冲突有效地激发出来。合理的矛盾冲突，可以充分调动初中生的学习欲望和兴趣，使学生学会正视自我，进行深入反思和思考，了解自身的学习情况。《论语》中说：“吾日三省吾身”，也是这个道理。矛盾冲突的科学应用，赋予了数学教学新的魅力和内涵，对学生自信心的引导有着很大的帮助，使学生体验到满足感。

矛盾冲突在初中数学课堂教学中主要分为两大类，即知识引入矛盾冲突和新知识探究矛盾冲突。

一、合理引入矛盾冲突，能够调动学生的自主学习性

数学教学注重对学生的思维引导，通过思索和探究拓宽学生视野，使学生从多方面接触数学知识，并进行合理应用。只有教育道路上经历艰难之路，才能培养学生聪颖、好学、上进。教育理论也要求在培养学生能力的同时，须培养学生的探究心理，使其善于发现身边事物并进行深入研究，通过知识学习构建精神世界。数学课堂教学内容的设计，对于教学水平的提升有很大的影响，对学生探究方向的引导也发挥着一定的作用。教师应设置教学引入环节，将学生在学习中遇到的困惑以及诱发的矛盾冲突带入教学，营造自我探究的环境，让学生在丰富的知识海洋中徜徉和探索，感受科学的魅力，自主学习能力也会得到很大提升[1]。

二、探究教学中引入矛盾冲突，能够激发学生的学习潜能

问题导入和训练是学生学习数学知识的基础。在初中数学教学知识导入过程中，会与旧知识发生一定的矛盾冲突。学生在理解数学知识时会形成矛盾意识，此时在探究式教学中引入矛盾冲突，可以引导学生形成较为完整的知识体系。很多数学知识看似有一定的逻辑关系，但学习起来又不太符合逻辑判断思维，从而使学生在思考时存在一定的困惑，在认知过程中又形成矛盾冲突。数学教师即可以利用知识矛盾点，引导学生自主探究[2]。

矛盾冲突的设置，需要数学教师提前设计好内容，做好课前准备，合理掌控课堂节奏，使各教学环节层层递进，把握每一个教学环节，使学生在矛盾冲突发生时能够从容应对，并合理利用矛盾冲突带来的探究机会以提升学生的综合能力和素养。

例如，勾股定理相关知识教学中，教师如直接向学生讲解勾股定理的概念，学生很容易感到困惑，甚至产生疑虑。此时，教师可设置合理的矛盾冲突，如图1所示：用几个小方块拼接成正方形，图中两个标黑色的三角形可以拼接成一个正方形，教师可以结合教学知识引入勾股定理知识，即直角三角形两个直角边平方的和与斜边平方的数值相等，用a、b表示两个直角边，c表示斜边，则可以了解勾股定理的公式为a²+b²=c²。通过矛盾冲突的设定，来引导学生掌握勾股定理知识[3]。

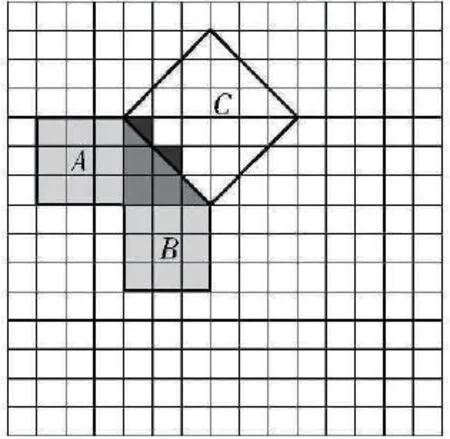
图1

三、合理利用矛盾冲突理论，拓展学生的思考范围

初中生在学习数学知识过程中，经常会遇到“简”和“繁”的矛盾冲突。对于同一问题，学生可以从不同的角度进行思考，找到解答问题的不同方法。有的方法比较直观快速，有的方法比较绕弯，其产生的效果也会有所不同。有些学生直接找到最简单的方法，有些学生经过繁杂的推算找到解答方法。简单与复杂的方式，对于初中生来讲都是收获知识的过程。在此过程中，学生思维方式发生了一定改变，开阔了视野，对知识的理解从表面到内部逐渐深入，经过研究和总结，可以找到最优、最快速的解题方式。

例如，开展几何图形相关知识教学中，教师应引导学生对抽象知识进行深入理解，全面掌握图形性质、概念，并与其他知识相结合，使学生的基本知识技能有所提升，从而对数学知识有更加深入的理解，通过透视图形，拓展知识面。

例如，证明三角形内角和定理过程。

方法1：如图2所示，△ABC中，延长BC至点D，经过点C做CE，使EC平行于AB。由于同位角相等，则∠B与∠ECD相等，且根据内错角相等，则∠A与∠ACE相等。因此，可以得出∠ACB+∠ECD+∠ACE为180°，将角进行替换可得出∠ACB+∠A+∠B为180°，通过以上推算得出三角形三个内角之和为180°。

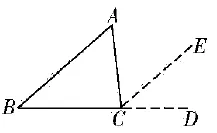
图2

方法2：如图3所示，△ABC中，过点C作直线BA的平行线CD，结合内错角相等定律，可以了解到∠A与∠1相等。由于CD平行于BA，则∠B+∠1+∠ACB等于180°。由此可以推算出∠A+∠B+∠ACB等于180°。

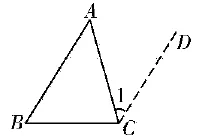
图3

通过以上研究可知：三角形内角度数证明可以有多个推算方法，其不仅可以利用平行线作为辅助进行推算，还可以通过绘制外接圆的方式进行推算和证明。多样化的推算方法以基础数学知识为核心，围绕知识定律和特点开展推导式学习。使学生通过多样化的推算，可以了解三角形内角的基本性质特点，并掌握其特点的推算方法，从而激发学生学习数学知识的兴趣，感受数学知识的神奇。除此之外，学生在证明过程中，也可以穿插应用多个数学知识，充分体现知识的互通性，从而加强知识的综合性，进一步巩固知识，拓展解题思路，探索新的学习方式。

结 语

综上所述，教师开展数学课堂教学时合理应用矛盾冲突的方式，可以引导学生学会自我探究，提升独立学习能力，并使数学课堂氛围更加活跃、轻松，赋予数学课堂以更多的活力。学生也可以通过对知识点的探究，了解自己学习中存在的不足，走出学习的误区，拓展思维方式，学会正确对待矛盾冲突，并通过问题解答，使思维得到碰撞，引导学生全身心地投入数学学习，加强多样化的学习体验，从而满足学生对知识的需求，挖掘内在潜力，以感受数学的学习魅力。