低围压下埕北海域重塑粉土动强度特性

肖 晓, 冯秀丽, 姜 波, 冯智泉

(1.中国海洋大学环境科学与工程学院,山东青岛 266100; 2.海底科学与探测技术教育部重点实验室,山东青岛 266100;3.中国海洋大学海洋地球科学学院,山东青岛 266100; 4.珲春市水利局,吉林珲春 133300)

近年来,海洋油气资源的勘探与开发受到各界学者的重视,中国也迎来了海底油气管道建设大发展、大跨越的新时期[1]。山东埕北海域海底管道密集,约有输油管道160段,总长280 km[2],是海洋油气资源开发的重点区域。这些油气管道常铺设在海底面0～5 m的土层中,处于低围压应力条件下。粉土是该区域的主要地基土质类型。海底粉土比黏性土更容易液化,在波浪荷载的循环作用下,易发生变形和破坏,导致管道泄漏等事件,且波浪对海底管道的局部冲刷会造成管道周围的粉土流失,形成管道悬空,造成管道的损坏[3]。因此,粉土的动强度特性直接关系到海洋油气管道的稳定性。许多学者借助室内动三轴试验,研究了不同条件下不同类型的土的动力特性。田竞等[4]利用KTG动三轴仪,分析了不同动强度影响因素的动荷载作用下粉土在不同围压下的动应力-动应变发展规律;赖夏蕾等[5]利用GDS 动三轴仪,研究了不同围压下淤泥质土在循环荷载作用下的动应变、动强度特性;唐杰鑫等[6]利用SDT-10动三轴仪器进行了低频振动下粉土的动力特性试验研究;孟凡丽等[7]利用TAJ-20动三轴仪器对饱和粉土动力特性进行研究;刘会欣[8]、卢成原等[9]等发现相同围压下,动应力和动剪切强度与破坏振次有良好的对应关系;冯秀丽等[10]、叶银灿等[11]通过内摩擦角和内聚力研究50、75 kPa围压条件下粉土的动强度,发现动强度值小于静强度。这些研究多是集中在50 kPa及以上较高围压条件下的,对于海底管道等埋深较浅的低围压条件下的海洋工程的适用性尚未可知。笔者研究低围压条件下粉土的动强度特性,以更好地服务于管道等埋深较浅的海洋工程建设。

1 试样制备与试验方法

1.1 试样制备

试验用土均采自埕北海域,为了便于控制土体的物理力学性质,试验中使用扰动样进行研究,扰动样的制备方法按照《土工试验规程(SL237-1999)》[12]中规定的方法进行。配制成黏粒质量分数分别为8%、10%和12%的粉土,各粒级分布状况如表1及图1所示。

表1 试验土样颗粒组成

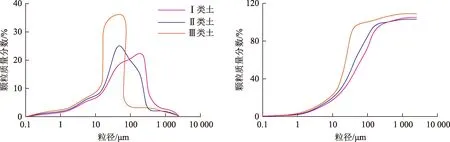
图1 土样颗粒频率及概率累积曲线Fig.1 Frequency and probability accumulation graphs of soil samples

参考研究区典型土体的物理力学性质,试验所用土体的力学性质如表2所示。

表2 土样基本力学性质

1.2 试验方法

试验在中国海洋大学海底科学与探测技术教育部重点实验室的英国GDS公司生产的伺服电机控制的动三轴试验系统(DYNTTS)上进行(图2),该仪器最大围压为1MPa,最大振动频率为5Hz,动态轴压分辨率小于1N,位移分辨率为0.20μm,轴向力测量精度高于0.1%,轴向位移测量和控制精度为0.07%,并专配高精度孔压传感器,精度达到0.1%(量程为 10kPa)。与传统动三轴系统相比,该系统具有精度高、稳定性好等优点。

采用固结不排水振动三轴试验,将配土制成直径38mm、高76mm的重塑土样,利用反压饱和法,使试样孔压系数高于0.95,然后将试样均压固结12h,再使用正弦式振动方式振动至土样破坏。

图2 动三轴试验系统Fig.2 Dynamic triaxial test instrument

2 试验结果与分析

2.1 破坏准则选择

选择科学合理的破坏准则是研究土体动强度的关键,目前常用的破坏准则有两种:一是孔压标准(即孔压和围压相等时视为土体发生破坏),二是应变标准(即动应变达到5%或10%时视为土体发生破坏)。但多项研究表明[8,13],并不是所有的土体都适用于某一个标准,例如对于某些土体,孔压并未达到围压值就已经产生了很大的轴向变形,若采用孔压标准势必会对试验结论产生很大的影响。因此,如图3所示,绘制了3类粉土的应变—循环振次、孔压—循环振次曲线,以便合理科学地确定试验粉土的破坏准则。

图3为Ⅰ类(黏粒质量分数8%)、Ⅱ类(黏粒质量分数10%)、Ⅲ类(黏粒质量分数12%)粉土在有效围压30kPa下应变和孔压随振次变化的关系曲线。由图3可看出,3类粉土轴向应变随振次发展规律相近,均是先缓慢增加,当轴向应变达到某一值时再迅速增加,有明显的转折点,指示土体发生破坏的趋势。3类土体的孔压随振次发展的规律也基本一致,均是先迅速增加,当孔压增到到某一特定值后趋于稳定;不同的是,Ⅰ类和Ⅱ类粉土最终的孔压可以达到有效围压30kPa,而Ⅲ类粉土的最终孔压小于有效围压30kPa。

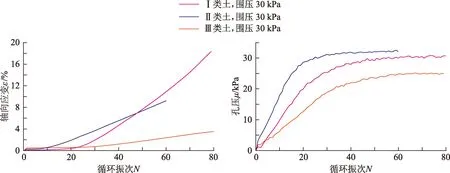
图3 3类粉土应变和孔压随振次变化关系Fig.3 Relations between strain & pore pressure and vibrations of three types of soils

为了进一步合理地确定低围压粉土的破坏准则,将试验部分土体的轴向变形拐点值、最终孔压比(最终孔压/有效围压)和最终孔压比时所对应的轴向变形值进行统计,见表3。由表3可看出,低围压应力条件下应变拐点值出现较早,介于1.0%～2.0%;Ⅰ类粉土、Ⅱ类粉土孔压比较大,介于0.90～1.00,Ⅲ类粉土孔压比较小,介于0.70～0.90;3类粉土达到最终孔压比时所对应的应变变化较大,介于2.3%～5.3%。由此可见,在低围压条件下采用以往经典的孔压标准或应变标准是不科学的,因为在低应力条件下应变拐点值出现的普遍早于达到最终孔压比时的应变,且土体破坏时,最终孔压达不到有效围压,动应变也未达到5%。

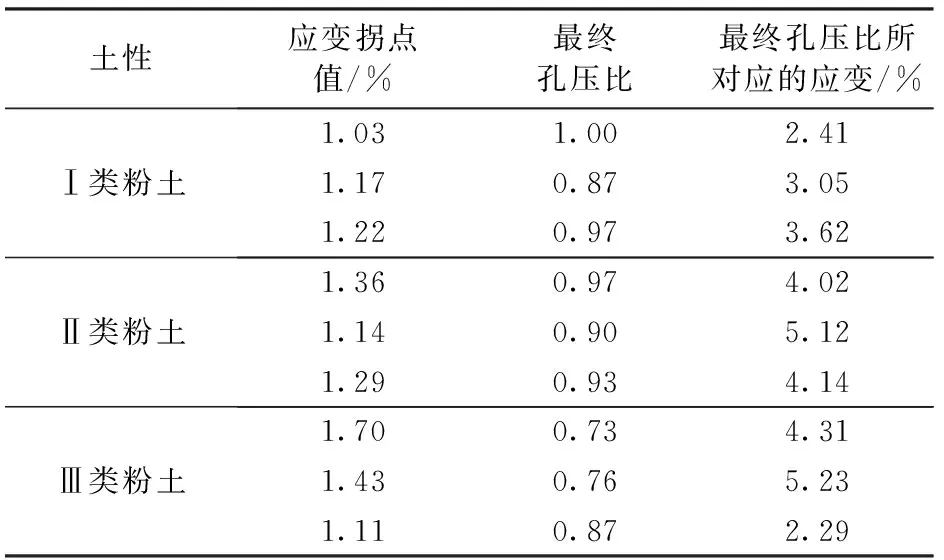
表3 土体应变孔压统计

为更进一步科学合理地确定粉土的破坏准则,绘制了达到破坏土样的q-p′图(q为偏应力，p′为有效主应力)及其所对应的轴向应变和循环振次关系曲线,发现两者有良好的对应关系。图4为其中一个样品的q-p′曲线及其所对应的轴向应变和循环振次关系曲线。

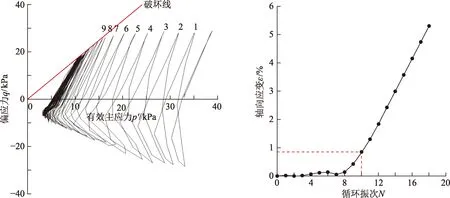
图4 典型粉土q-p′曲线及其轴向应变与循环振次关系Fig.4 q-p′ curve of typical silt and relations between axial strain and cyclic vibrations

由图4可看出,低围压条件下粉土q-p′曲线呈蝴蝶式典型特征,并有随循环振次逐渐逼近于破坏线的趋势(图4左图),在循环振次1～9之间,粉土q-p′曲线在破坏线之下,指示土体处于弹性应变范围内,土体并未发生破坏,体现为较小的轴向应变,一般小于1%(图4右图);当循环振次达到10次以后,土样q-p′曲线与破坏线相交,轴向应变也随循环振次增加而迅速增大,土样破坏。在试验粉土中,选择具有代表性的10个粉土样品,统计了它们的q-p′曲线与破坏线相交时的破坏振次与其所对应的轴向应变数据,如表4所示。

可见绝大部分粉土样品破坏时,轴向应变接近2%,不超过3%。因此,综合最终孔压比和轴向应变两个参数,提出了低围压条件下的破坏准则:①对于黏粒质量分数小于10%的粉土(Ⅰ类粉土),将孔压比达到0.9作为粉土破坏准则;对于Ⅲ类粉土,将孔压比达到0.7作为粉土破坏准则;②粉土轴向应变达到2%～3%作为粉土破坏准则。

这两种参数下破坏准则并不矛盾,因为当Ⅰ类粉土和Ⅲ类粉土的最终孔压比分别达到0.9或0.7时,粉土轴向应变也达到了约3%。值得说明的是,本次试验分别确定了以最终孔压比和轴向应变为参数的低围压下粉土的两种破坏准则,是因为粉土的黏粒质量分数变化范围较大;在实际试验中,土体的破坏临界点的确认很模糊。最终孔压比和轴向应变两个参数在试验中相互影响较小,但得到的土体破坏临界点基本一致,它们能够更明确地确定低围压条件下粉土的土体破坏准则。

2.2 低围压粉土动应力曲线特性

土的动强度是在一定动荷载作用次数下产生某一破坏应变所需的动应力。在相同试验条件下(相同围压和应力比),分别施加3～5 个不同的动应力进行动强度试验[14]。通过对动三轴试验数据处理,并结合所确定的土体破坏准则,得到动应力幅值与循环破坏振次的关系曲线,该动应力曲线可用来反应低围压下粉土的动强度。本次试验针对3类粉土在不同有效围压下进行试验,动应力曲线如图5所示。

由图5可看出,低围压下粉土动应力曲线遵循较一致的变化规律:即动应力幅值随破坏振次增加而降低,且当破坏振次较小时,动应力幅值衰减速度较快;当破坏振次逐渐增大时,动应力幅值衰减速度减缓,曲线趋于平缓。对图5中低围压下粉土动应力曲线进行幂函数拟合,发现所有幂函数的拟合相关系数R2均大于0.93,具有显著的幂函数相关性。由此可得到:低围压条件下粉土的动应力曲线遵循幂函数的曲线规律,其一般表达式为

(1)

式中,σd为动应力振幅,kPa;Nf为循环破坏振次;a、b为与试验土样性质和有效围压相关的两个常数。

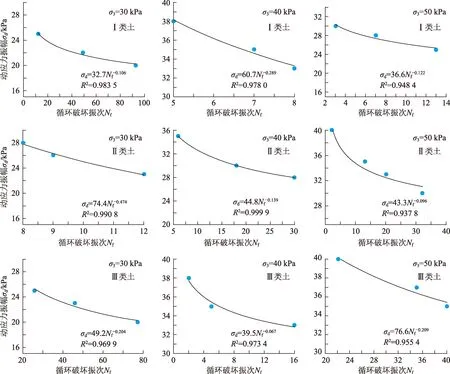
图5 低围压下3类粉土动应力曲线Fig.5 Dynamic stress curves of three types of silts under low confining pressure

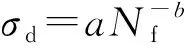
低围压条件下粉土动应力曲线与一般围压条件下相比,均具有幂函数式的变化规律,低围压条件并未影响粉土动应力曲线的总体形态,仅对拟合幂函数曲线中的a、b常数取值有一定影响。总体来说,低围压条件下a、b取值较一般围压条件下大,使拟合曲线呈现较陡峭趋势。这可能是由于低围压条件下土体内部颗粒联接不够紧密,在循环振动下较易发生破坏。

2.3 固结比对低围压粉土动强度影响

影响土体动强度的因素有效围压、孔隙比、饱和度、固结比、振动频率、含水率、土颗粒粒径和形状及土的结构性等[16]。目前对土体动强度影响因素的研究多集中于探讨土结构、有效围压、振动频率和固结比对土体动强度的影响[17-20],其中对低围压小于50 kPa条件下的固结比对粉土强度的研究较少涉及。

图6为3种黏粒质量分数的粉土在不同固结比条件下的应变随循环振次变化的关系曲线。

由图6可看出,3种黏粒质量分数的粉土在不同固结比下表现出较为一致的变化规律:即在围压、动应力、荷载频率相同条件下,达到某一较大的特定振次时,固结比k=1.0的粉土轴向应变最大,动强度最小;其次为固结比k=2.0的粉土,轴向应变最小的是固结比k=1.5的粉土。由此可见:低围压条件下,在固结比为1.0～2.0,粉土的动强度随固结比增大具有先增大后减小趋势,动强度的最大值出现在固结比为1.5附近。这可能是由于适当增加轴向压力可以使土体更加密实,从而有助于增大土体的动强度;但当轴向压力超过某一极限值时,这一轴向压力相反会破坏土体原有的稳定结构,致使土体的动强度有所减小[21-23]。

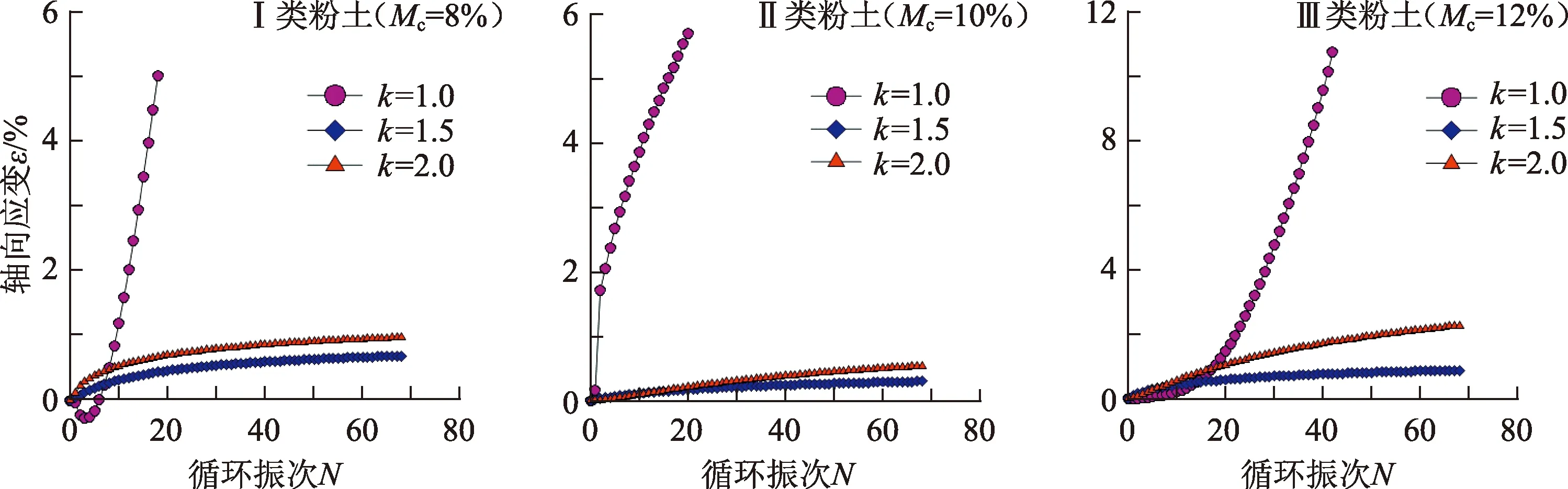
图6 不同固结比下粉土轴向应变-循环振次曲线Fig.6 Axial strain-cycle vibrations curves of silt under different consolidation ratios

2.4 低围压粉土内摩擦角和内聚力

同种土在不同的试验条件、试验方法和不同仪器下测得的结果往往差距很大,给工程建设埋下了较大的安全隐患[24]。通过动应力曲线(图5)确定某一固定破坏振次时不同围压σ3条件下的动应力幅值σd,利用σd+σ3确定垂向最大主应力σ1,进而根据σ3和σ1绘制摩尔应力圆。因本试验中共有30、40、50 kPa三种围压条件,可绘制3个摩尔应力圆,再做3个应力圆的公切线,切线与x轴的夹角即为内摩擦角φ,切线与y轴的截距即为内聚力c。图7为循环破坏振次为40时,黏粒质量分数12%的Ⅲ类粉土的抗剪强度包线,据此求得内聚力c=1.83kPa,φ=12.64°。依据此种方法求得3类粉土在不同循环破坏振次时的φ和c,见表5。

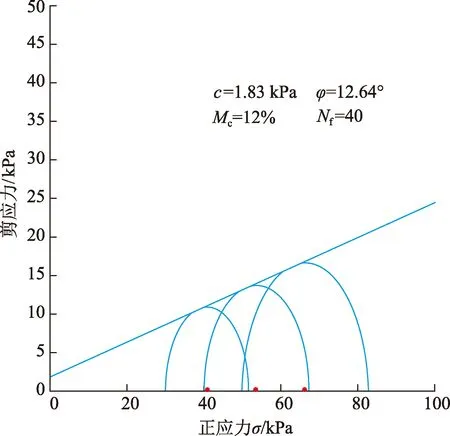
图7 Ⅲ类粉土抗剪强度包线Fig.7 Shear strength envelope of silt of type Ⅲ

由表5可看出,粉土的内摩擦角介于8.6°～ 15.26°,内聚力介于1.20～4.86 kPa。结合本区的其他研究,对于黏粒质量分数介于8%～12%的埕北海域粉土,以往静三轴试验所获得的φ介于16.3～32.3°,c介于7.89～27.05 kPa[8];在一般围压下(有效围压大于50 kPa),固结不排水振动三轴试验所得到的φ介于4.1°～ 8.0°,c介于1.0～4.5 kPa[8],如图8所示。

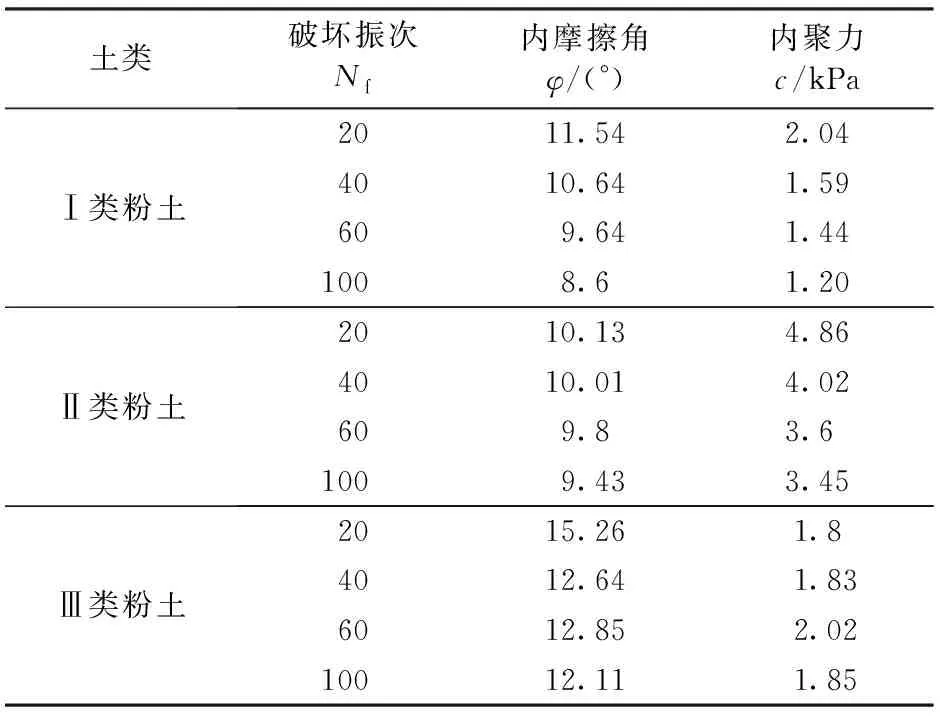
表5 低围压3类粉土φ、c统计Table 5 Statistics of φ and c of three types of silts at low confining pressure

动三轴试验所获得的φ、c一般远小于静三轴试验所获得的φ、c值。静三轴试验所获得的粉土φ约为动三轴试验的2～4倍,c值为1～3倍。对于不同围压下的动三轴试验所得到的c较为接近,但一般围压条件下(有效围压大于50 kPa)固结不排水振动三轴试验所得到的粉土φ普遍小于低围压条件下同类型试验。

通过φ、c值对比,粉土动强度比静强度要小许多,不同围压下粉土的动强度也不同。因此,在进行海底管道等浅表层工程建设时要注意这些参数的选择,不能一味地按照静强度和一般围压条件下的参数进行设计,否则有可能给浅层海洋工程的建设埋下安全隐患。

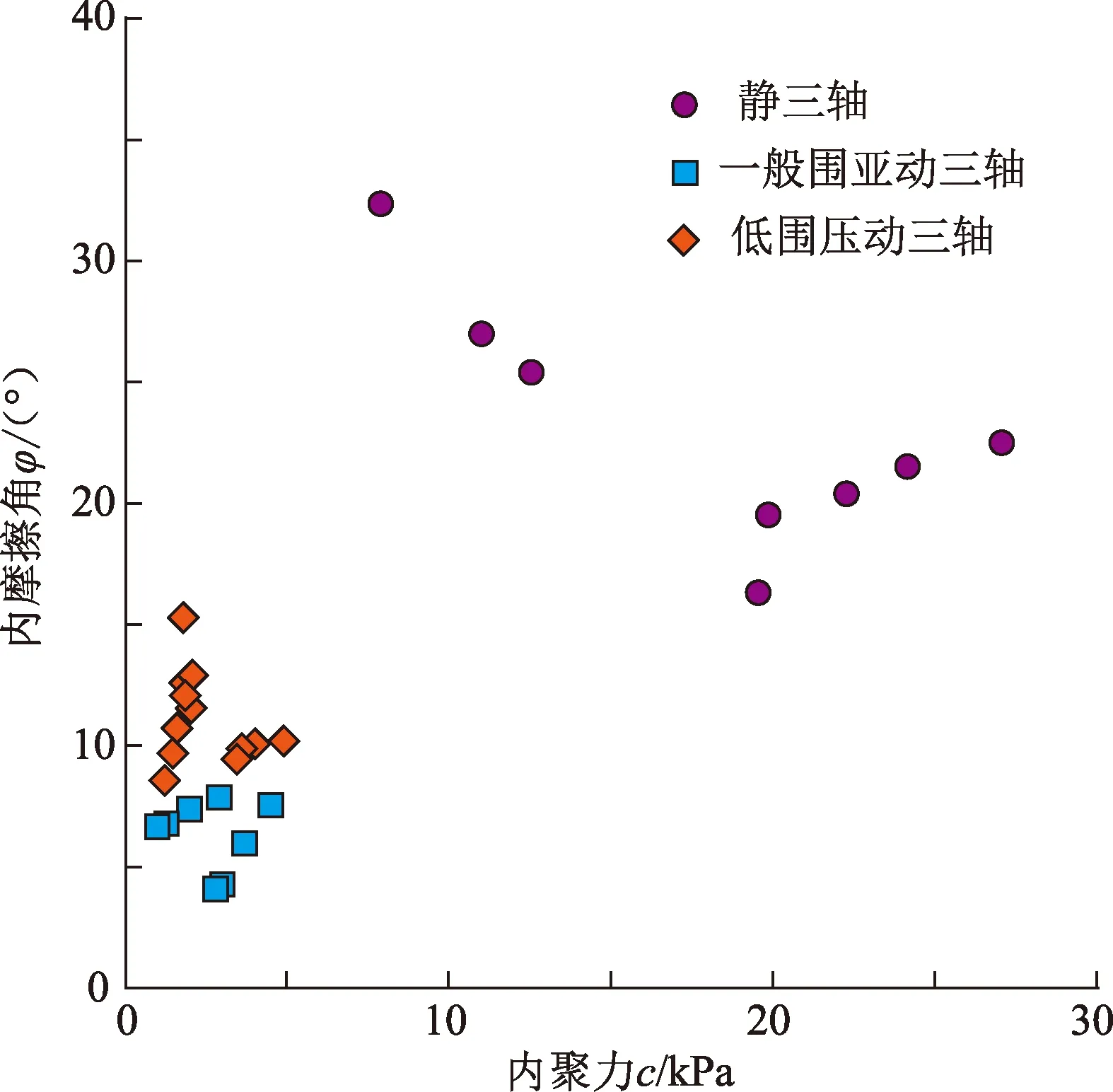
图8 不同试验条件和方法下φ、c对比Fig.8 Comparison of φ and c values under different test conditions and methods

2.5 临界循环应力比

当轴向循环动应力与轴向静力压强之比小于某一临界值时,试样的轴向应变随循环振次增加逐渐趋于稳定,土样不会发生破坏,并将这样的一个临界值称为临界循环应力比[25],表示为

(2)

式中,Kcr为临界循环应力比;σd为轴向循环动应力,kPa;σf为土体轴向静力压强,kPa。

海底土体在波浪作用下能否产生液化是海洋工程所关心的问题,海底粉质土液化的判别分为初判和复判2个阶段;初判以海床土体的临界循环应力比来判别,若土体循环应力比Kc≥Kcr时,则初步判定为液化[26],许国辉[27]利用动三轴对黄河三角洲粉土原状样的试验分析表明,在120 kPa围压下该区域粉土的临界循环应力比为1.58～1.70。

采用刘会欣[8]的方法,将临界循环应力的公式进行了改造,以此来研究低围压条件下埕北海域粉土的临界循环应力比。改造后的临界循环应力比表示为

(3)

式中,Kcr为临界循环应力比;σd为临界轴向循环动应力,kPa;σ1为轴向主应力,kPa;σ3为围压,kPa。

为了确定临界循环应力比值,对于黏粒质量分数相同的粉土在同一个围压下,通过改变轴向循环应力进行了不少于4个样品的试验。Ⅰ、Ⅱ、Ⅲ类粉土样品分别在30、40、50 kPa围压下均存在某一轴向循环动应力,当循环动应力大于该值时,随着循环振动次数增加,土体轴向应变逐渐增大,最终土体发生破坏;当轴向循环动应力不超过该值时,土体轴向应变很小,且随着振动次数增加,土体轴向应变稳定于某一较小值,土体基本维持在弹性应变阶段,不发生土体破坏。图9为Ⅰ类粉土在围压50 kPa下不同轴向循环动应力时轴向应变随振次变化的关系曲线。

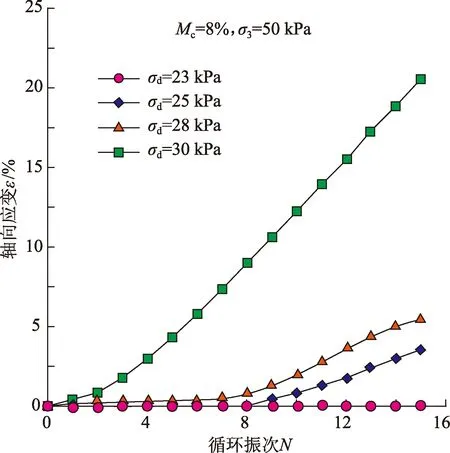
图9 Ⅰ类粉土50 kPa围压下轴向应变-循环振次曲线Fig.9 Axial strain-cycle vibrations curves of silt of type I under 50 kPa confining pressure

由图9可看出,试样的轴向应变随循环振次增大而增大,且当轴向循环动应力越大时,在相同振次条件下土样轴向应变越大,并能够在较短的循环周期内达到破坏;但当轴向循环动应力降至23 kPa时,试样的轴向应变随循环振次增加并无明显变化,无论循环振次增加到多少,试样轴向应变一直维持在某一特定值保持稳定,试样很难达到应变的破坏值。因此, Ⅰ类粉土在围压50 kPa条件下的临界循环应力为23～25 kPa。

依据该方法,将3种黏粒质量分数不同的粉土在不同围压下的临界循环动应力进行统计,并利用改造后的临界循环应力比公式计算了3种粉土的临界循环应力比,见表6。

由表6可知,不同黏粒质量分数的粉土在不同围压条件下所求得的临界循环应力比差值不大,基本介于1.46～1.75,从海洋工程建设及施工的安全方面考虑,将低围压下埕北海域重塑粉土的临界循环应力比确定为1.45。

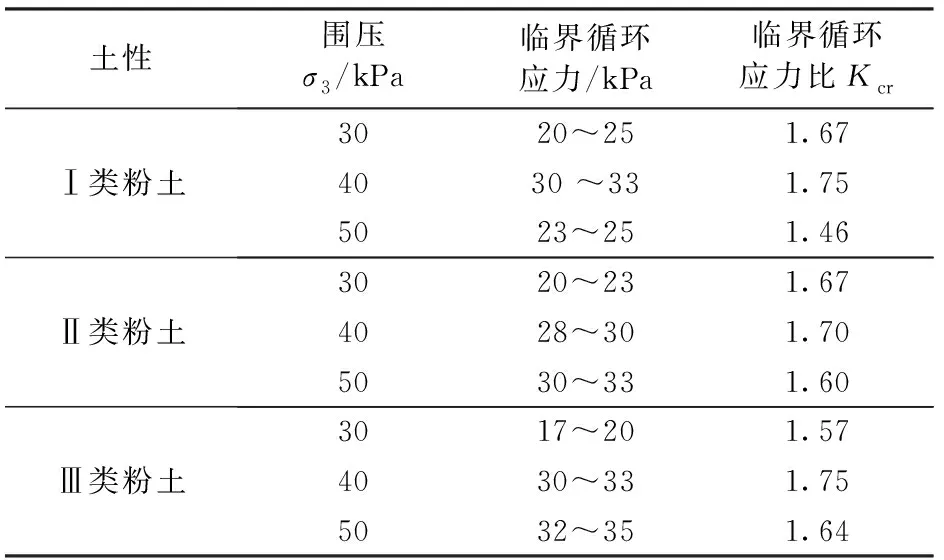
表6 粉土临界循环应力比统计

3 结 论

(1)低围压条件下粉土破坏点较一般围压条件下出现的早,将粉土轴向应变达到2%～3%;黏粒质量分数小于10%的粉土,孔压比达到0.9;黏粒质量分数大于10%的粉土,孔压比达到0.7作为低围压条件下粉土破坏的标准。

(2)低围压条件下粉土动应力曲线随破坏振次的增大呈现幂函数曲线缓慢衰减的规律。

(3)低围压条件下埕北海域重塑粉土的内摩擦角φ介于8.6°～15.26°,内聚力c介于1.20～4.86 kPa,比静三轴试验所获得的φ、c小许多,与一般围压条件下的动三轴试验所获得的φ、c相比,c变化不大,φ变化较大。

(4)低围压条件下随固结比增大粉土动强度先增大后减小,粉土动强度的最大值出现在固结比k=1.5附近。

(5)从海洋工程建设及施工的安全方面考虑,埕北海域重塑粉土的临界循环应力比为1.45。