缝洞型碳酸盐岩油藏流固耦合数值模拟
黄朝琴, 周 旭, 刘礼军, 黄 涛, 姚 军, 王晓光, HERVÉ Jourde
(1.中国石油大学(华东)油气渗流研究中心,山东青岛 266580; 2.法国国家科学研究中心水文科学所,蒙彼利埃 34095)
中国西部碳酸盐岩油藏油气资源丰富,其中缝洞型约占2/3,是增储上产的现实领域[1]。与孔隙型和裂缝型碳酸盐岩油藏不同,缝洞型油藏从储集空间到流动规律都有较大差异[2-5],传统的Darcy渗流理论已不完全适用[6]。对此,研究者提出了离散缝洞模型[7-8],采用Darcy-N-S(Navier-Stokes)方程来表征渗流-自由流耦合流动。缝洞型碳酸盐岩油藏埋藏深度超过5 300 m,为深层油气资源[9]。裂缝和溶蚀孔洞在开发过程中易发生变形,具有强应力敏感性[10-13]。Murad等[14]在Beavers-Joseph-Saffman(BJS)条件基础上,考虑岩石变形影响,将BJS条件扩展至流固耦合研究中。Badia等[15]应用扩展的BJS条件,基于有限元对Biot-N-S(Navier-Stokes)方程进行了数值研究,Ambartsumyan等[16]则通过引入Biot-N-S方程拉格朗日乘子来构造稳定有限元格式。Zhang等[17]针对缝洞介质提出了一种流固耦合计算格式,应用FLAC3D软件[18]开展了数值模拟研究。但其研究忽略了渗流-自由流界面上的切向流动;同时裂缝未采用几何降维处理,导致计算量大难以实际应用。对此,笔者建立离散缝洞流固耦合数学模型。多孔介质渗流区域采用Biot方程,并对裂缝进行降维处理,采用Galerkin有限元求解;溶洞中采用N-S方程,采用Taylor-Hood混合元方法求解;两区域间通过扩展BJS条件耦合。通过两个经典数值算例验证了模型和方法的正确性。在此基础上,通过实际缝洞型油藏算例对开采过程中的裂缝和溶洞变形及其对产量的影响进行研究。
1 离散缝洞流固耦合数学模型建立
缝洞型碳酸盐油藏一般经历了多期构造运动和岩溶作用[1],导致介质中发育着大量裂缝和溶蚀孔洞,如图1(a)所示。因此缝洞型储层介质为一复杂的离散缝洞模型,如图1(b)所示。在该模型中,基质岩块和裂缝组成渗流系统,为经典的离散裂缝模型,其中的流动满足Darcy定律;溶洞系统为自由流区域,流体流动采用N-S方程;两区域间采用BJS条件[19-20]耦合。

图1 缝洞型油藏岩心及离散缝洞模型示意图Fig.1 Typical core of fractured vuggy carbonate reservoirs and discrete fracture-vug model
1.1 渗流区域流固耦合模型
为进一步考虑渗流区域介质的变形影响,假设多孔介质渗流区域满足弹性小变形假设,并考虑微可压缩流体的等温单相流动过程,其流固耦合过程由以下方程予以描述[12]。
(1)平衡方程为
(1)
式中,σp为应力,以拉伸为正,下标p表示多孔介质区域;ρp、ρs和ρf分别为多孔介质、固体骨架和流体的密度;φ为多孔介质孔隙度;g为重力加速度。
(2)本构方程为
σ′=σp+αppI=C:εs.
(2)
式中,σ′为岩石有效应力;α为Biot有效应力系数;pp为孔隙流体压力;I为单位张量;C为固体骨架的弹性模量;εs为固体骨架的应变张量,满足以下几何协调方程。
(3)几何方程为

(3)
式中,us为固体骨架位移,εv为相应的体积应变。
(4)Darcy方程为

(4)
式中,v为多孔介质渗流速度;k为多孔介质渗透率;μ为流体黏度。
(5)连续性方程为

(5)
其中
式中,q为源汇项;Kf为孔隙流体的体积弹性系数(流体压缩系数的倒数);Ks为固体骨架的体积弹性系数;M为Biot模量,描述多孔介质体积不变的情况下,在流体压力作用下进入多孔介质中的流体[21-22]。
在弹性小变形条件下,弹性模量C和Biot有效应力系数α均可视为常数。孔隙度φ和渗透率k一般是有效应力的函数[23]。研究中所有的微裂缝(包括节理)和微溶孔均包含于基质岩块系统中,可视为等效的连续介质模型。对于宏观裂缝,如图2所示。

图2 实际粗糙裂缝简化示意图Fig.2 Schematic of a real rough fracture and the simplified conceptual fracture
由于裂缝壁面粗糙且相互接触,与此同时裂缝通常被其他物质充填[24];因此本文中将宏观裂缝视为狭长的高渗透区域,仍属于多孔介质渗流区域。然而,相对于整体缝洞介质研究区域的特征尺度,裂缝可简化为一个弹性薄层。为避免裂缝区域的大量精细网格剖分,本文中在几何上对裂缝采用降维处理[25],建立相应的离散裂缝流固耦合模型。
1.2 溶洞自由流区域流动方程
考虑溶洞中微可压缩流体的低雷诺数等温层流流动问题,满足下述方程。
(1)Navier-Stokes方程为

(6)
式中,uf和σf分别为溶洞中的流体速度和应力。
(2)本构方程为
σf=-pfI+2μεf.
(7)
式中,εf为流体应变张量,满足以下几何协调方程。
(3)几何方程为

(8)
(4)连续性方程为

(9)
1.3 渗流-自由流耦合界面条件
如图1(b)所示,在渗流-自由流耦合交界面Γpc上,需要引入相适应的界面条件。对于单一流场问题,一般采用BJS条件来耦合Darcy方程和N-S方程。对于流固耦合问题,需要在界面处进一步考虑多孔介质骨架变形的影响,根据质量和动量守恒定律可采用拓展的BJS界面条件[14,26-27],

(10)
式中,n和τ分别为渗流和自由流耦合交界面Γpc的单位法向量(指向渗流区域)和单位切向量;β为耦合交界面上的BJS速度滑移系数。
2 有限元数值求解
采用有限元方法求解上述离散缝洞流固耦合数学模型。其中渗流区域采用标准的Galerkin有限元方法,自由流区域采用Taylor-Hood混合元方法,裂缝采用降维处理。
2.1 渗流区域数值离散格式
对于渗流区域的Biot多孔弹性力学方程,数值计算格式以节点位移和压力为未知量,即us-pp格式[28]。采用标准的Galerkin有限元方法进行离散,则多孔介质区域流固耦合方程(1)和(5)离散后的有限元计算格式为
(11)
其中
式中,{us}为节点固体骨架位移列阵;{pp}为节点孔隙压力列阵;{fp}为多孔介质区域体积力列阵;{qp}为多孔介质区域流体体积力和源汇项列阵;变量符号上面的点表示对时间的一阶导数;Kp为多孔介质固体骨架的标准刚度矩阵;B为应变-位移矩阵;D为排水条件下的岩石固体骨架材料常数矩阵;L为多孔弹性介质的流固耦合矩阵;对于三维问题α=α[1,1,1,0,0,0]T,二维问题α=α[1,1,0,0]T,称为Biot有效应力系数列阵;H为渗透矩阵;N为形函数向量;Ms为多孔介质流体储集矩阵。
上述方程系统可采用标准的向后差分时间格式进行离散和求解,详细的推导和求解过程可参考文献[28]。
2.2 自由流区域数值离散格式
对于自由流区域,需要联立求解方程(6)和(9),由方程(6)可知速度插值函数最好比压力插值函数高一阶,以达到较好的计算精度[29]。对此应用加权残量法推导有限元方程,采用经典的Taylor-Hood混合单元(Pn-Pn-1)构造插值函数[28-29],具体表达式为

(12)
式中,I和J分别为速度与压力单元节点数;Nu和Np分别为速度和压力的形函数。
对于微可压缩流体的等温流动过程,可忽略流体密度的变化,因此在自由流区域可采用不可压缩流体流动的Navier-Stokes方程,离散后的数值计算格式为
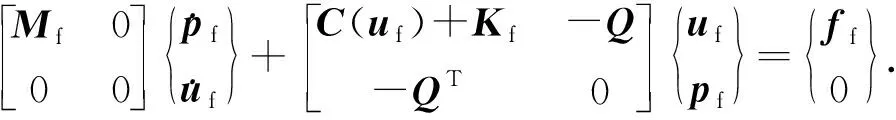
(13)
其中



式中,{uf}为节点的流体速度列阵;{pf}为节点的流体压力列阵;{ff}为自由流区域载荷列阵,包括体积力和外边界给定的应力边界条件;T为自由流区域给定的应力边界条件。
上述方程系统(13)式可采用标准的向后差分时间格式进行离散和求解,详细的推导和求解过程可参考文献[29]和[30]。
2.3 离散裂缝数值离散格式
如前所述,实际裂缝可视为一狭长的高渗透多孔介质区域。在数值处理中,对于渗流场可通过等效流量原理对裂缝进行降维处理,目前已有大量相关研究[3-5]。对于应力场,裂缝单元开度d和单元长度l相比,往往相差多个数量级。此时,类似于离散裂缝渗流模型中的等效流量原理,可将应力场中的裂缝也进行降维处理,如图3所示。此时,相应的变形刚度矩阵为
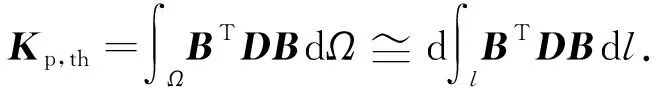
(14)
其中下标th表示薄层裂缝。当d/l的比值取值在0.01~0.1时可取得较高的计算精度[32-33]。对于方程(12)和(13)中的其他项可进行类似的处理,对于三维问题,裂缝降维后为一裂缝面,将出现两个方向的单元长度l。此时,裂缝单元开度d应和单元长度l较小的方向取比值进行分析。
(15)

图3 裂缝薄层单元简化示意图Fig.3 Schematic of a simplified fracture thin-layer model
多孔介质流固耦合方程(11)和自由流区域方程(13)通过引入交界面边界条件方程(10)即可形成缝洞型介质的流固耦合数值计算格式。对两方程采用相同的时间离散格式,本文中采用向后差分格式,可得到最终的有限元计算格式。
3 数值算例分析
3.1 数值验证算例
3.1.1 流固耦合验证算例
考虑如图4所示的一维固结问题,该物理过程可分解为两个阶段:第一阶段,在多孔介质上表面瞬时加载均匀载荷,为非排水过程,导致孔隙压力升高;第二阶段为排水阶段,压力逐渐降低,垂向位移持续增加。本算例模型为1 m×1 m×100 m(x×y×z),采用结构化网格剖分,网格尺寸为0.5 m×0.5 m×0.5 m(x×y×z)。其他计算参数取自于文献[12]7.5节中的Berea砂岩试验数据,上覆施加载荷为0.1 MPa。由于排水和非排水过程存在一定的差异,两者之间的主要差别在于是否考虑流体流出,前者没有流体流出,因此测量得到的泊松比并不一样,具体参数取值为:剪切模量G=6 GPa,泊松比ν=0.2(排水),泊松比ν=0.33(不排水),孔隙度φ=0.19,渗透率k=1.875×10-13m2,弹性模量E=14.4 GPa,拉梅常数λ=4 GPa,Biot模量M=12.25 GPa,Biot有效应力系数α=0.79,流体可压缩系数Cf=3.5×10-10Pa-1,流体黏度μ=1.0 mPa·s。
图5为第二阶段排水过程中本文数值解与解析解的对比。显然,两者具有很好的一致性,验证了本文中多孔介质区域流固耦合数值计算的正确性。

图4 一维固结物理过程示意图Fig.4 Schematic of 1D consolidation process

图5 一维固结问题数值解与解析解的比较Fig.5 Comparison of pore pressure and vertical displacement between numerical results and analytical solutions
3.1.2 渗流自由流耦合验证算例
该验证模型采用经典的Beavers-Joseph试验模型[18,32],如图6(a)所示。考虑自由流-渗流稳定耦合层流问题,pin=0.5 Pa,pout=0 Pa,模型长度L=0.5 m,高度h=0.1 m,两区域的压力梯度为1.0 Pa/m,渗流区域的孔隙度为0.2,渗透率k=1×10-12m2。
为简化计算,流体的密度取值为1 kg/m3,黏度为1 Pa·s,在交界面上BJS速度滑移系数β取值为1.0。有限元计算采用如图6(b)所示的结构化网格剖分,并在自由流-渗流交界面处网格加密。图7为本文数值解和解析解的对比,两者基本吻合,验证了渗流自由流耦合数值计算的正确性。详细的解析解形式可参考文献[20]和[21]。

图6 渗流-自由流耦合流动Fig.6 Schematic of coupling porous-free flow system and its structured meshing

图7 本文数值解与解析解对比Fig.7 Comparison between analytical solution and numerical solution
3.2 缝洞介质流固耦合算例
考虑如图8所示的碳酸盐岩缝洞型介质模型,该模型整体处于奥陶系,顶深为5500 m,右端溶洞与两条正交裂缝相连通,模型的右下端存在底水能量补充,生产井钻遇左端溶洞并进行定压生产(45 MPa)。模型的初始流体压力、上覆压力和右侧水平侧压均由图9地应力深度分布曲线计算得到,其中右侧水平侧压取为最大水平主应力。图9中的数据取自现场测试数据和文献中数据[35-38]。多孔介质区域的左端和底部均为滑动边界。
实际生产过程为油水两相流动,本文中模型仅考虑了单相流动,具体计算参数为:流体密度ρf=870 kg/m3,固体骨架密度ρs=2 650 kg/m3,流体黏度μf=20 mPa·s,固体骨架弹性模量Em=48 GPa,裂缝弹性模量Ef=24 GPa,泊松比ν=0.27,基质岩块孔隙度φm=0.09,裂缝孔隙度φf=0.5,基质岩块渗透率km=1×10-14m2,裂缝渗透率kf=1×10-10m2,BJS速度滑移系数β=1.0,Biot有效应力系数α=0.79,流体可压缩系数Cf=5×10-10Pa-1,剪切强度τn=80 MPa。其中基质岩块包含了微小裂缝和溶蚀孔洞,其渗透率取值大于实际纯基质的渗透率。图10为流固耦合效应对产量的影响,计算中采用三角形单元进行网格剖分(图11(a)),包含19 072个单元,其中多孔介质区域采用二次插值函数单元,溶洞区域采用P2-P1型Taylor-Hood单元。

图8 缝洞型介质几何模型及约束加载图Fig.8 Geometry and constraints of the fractured vuggy medium

图9 地应力与孔隙压力随深度变化曲线Fig.9 Variation of stress and pore pressure with depth

图10 不同模型的产量对比Fig.10 Comparison of productions between different models
如图10所示,由于井打在溶洞上,生产井日产量初期很高,但由于能量补充不足迅速下降;对于流固耦合模型,由于充分考虑了固体骨架的变形作用,使油藏的供液能力在初期有所提高,因此其初期日产量和累积产量相比于不考虑流固耦合效应的纯流动模型均有所提高。但随着开采的进行,由于孔隙压力的降低,固体骨架进一步变形导致多孔介质区域的孔隙度及渗透率降低,使井的日产量和累积产量均低于不考虑流固耦合效应的纯流动模型。计算中,基质岩块的孔隙度和渗透率变化与平均应力相关[39-40],表达式为

(16)

对于裂缝,孔隙度仍采用式(16),但渗透率与裂缝开度变化相关[40],表达式变为

(17)
式中,kf0为裂缝初始渗透率;c1为经验参数(本算例取值0.071 2);Δd为裂缝开度变化量。
图11(b)中给出了耦合模型计算达到稳定后的压力云图和速度矢量分布,计算结果显示流体在溶洞中的流动速度较快,可近似处理为等势体;多孔介质区域中裂缝作为高导流通道对压力和速度也有显著影响。图11(c)中给出了围压状态下最大主应力和最小主应力的差值云图,可看到在该荷载工况下,裂缝尖端具有明显的应力集中,但溶洞的应力集中部位并非都出现在其顶部和底部,采用Tresca强度准则进一步分析其剪切破坏区域,

(18)
式中,σ1和σ3分别为最大和最小主应力;τ为岩石所受的剪切应力。
破坏程度F计算公式为

(19)
式中,F为破坏程度,F≥1,表示岩石已发生剪切破坏或临界破坏区域,F<1,表示未发生破坏;τn为岩石的剪切强度。

图11 缝洞型介质流固耦合算例结果Fig.11 Results of hydro-mechanical process for fractured vuggy medium example
根据上述判定准则可得到岩石剪切破坏区域分布,如图11(d)所示。破坏区域主要集中于裂缝尖端和溶洞尖点区域。计算中宏观裂缝的初始开度均为0.05 m,压力场稳定后,垂直裂缝开度平均增加0.026 m;水平裂缝开度平均减少0.036 m,闭合程度较高。该结果表明,水平裂缝与左端溶洞破坏后相连通,这对于沟通缝洞结构体有利,但裂缝的闭合对其连通程度也有降低作用,同时破坏区域的储渗参数变化也有重要影响,因此破坏区域对流动的影响需综合考虑和研究。
4 结 论
(1)针对深层缝洞型油藏的强应力敏感性,创建了离散缝洞模型的流固耦合数学模型,其中多孔介质渗流区域采用Biot方程,溶洞区域视为自由流区域采用N-S方程,两区域间采用扩展的Beavers-Joseph-Saffman边界条件进行耦合。采用有限元法对Biot-N-S(Navier-Stokes)流固耦合数学模型进行了数值离散:渗流区域采用经典Galerkin有限元方法;自由流区域采用Taylor-Hood混合元方法。裂缝采用几何降维处理以提高计算效率:在流场中,裂缝为高渗流通道;在应力场中,裂缝处理为薄层单元。通过一维固结和Beavers-Joseph实验模型两个数值算例验证了模型和数值方法的正确性。
(2)溶洞中的压力传播速度较快,相对于渗流区域可视为一流动等势体。在降压生产过程中,裂缝尖端和溶洞附近区域易发生较大面积的破坏,而较高的流体压力对于溶洞和裂缝壁面具有一定的支撑作用;因此在此类油气藏的开发中应适当采取保压措施,以避免溶洞坍塌和裂缝闭合。

