基于DLVO理论的低矿化度水驱对岩石润湿性的影响

崔传智, 韦自健, 吴忠维, 杨 勇, 黄迎松, 吕广忠, 曹 刚

(1.中国石油大学(华东)石油工程学院,山东青岛 266580; 2.中国石化胜利油田分公司勘探开发研究院,山东东营 257015)

低矿化度水驱作为一项经济可行的精细化注水技术,能有效地改变岩石润湿性,降低残余油饱和度[1],可提高4%～38%的原油采收率[2-4]。低矿化度水驱涉及岩石-水膜-原油界面间的相互作用,是多物理化学场之间的耦合,渗流规律和增产机制复杂,其机制主要包括润湿性转变、微粒运移、类碱驱的pH值升高与界面张力降低、多官能团离子交换、双电层膨胀等[4-9]。其中润湿性改变是最主要的提高采收率机制。研究人员从宏观上探究了低矿化度水驱对界面Zeta电势与岩石润湿性的影响规律[4-13],其研究大多局限于对实验规律的解释,笔者基于胶体稳定性(DLVO)理论和扩散双电层理论,建立岩石-水膜-原油系统分离压力数学模型,从微观受力角度对分离压力影响因素进行敏感性分析,明确润湿性改变的主控因素。结合Young-Laplace方程和相互作用势能理论,计算不同低矿化度水驱下稳定水膜厚度和岩石润湿角,预测岩石润湿性随低矿化度水驱的变化规律。

1 DLVO理论与水膜稳定性

在砂岩油藏注水开发过程中,聚集在岩石颗粒间空隙处的油滴与附着在岩石颗粒表面的水膜构成了如图1所示的岩石-水膜-原油系统。岩石-水膜-原油系统为热力学平衡体系,岩石-水膜和水膜-原油界面间存在着多种复杂的物理化学反应,这些反应影响着水膜稳定性[14]。水膜稳定性与岩石润湿性密切相关,水膜越厚越稳定,岩石水湿性越强。

图1 砂岩油藏与岩石-水膜-原油系统微观结构Fig.1 Microstructure of sandstone reservoir and rock-brine-oil system

砂岩黏土颗粒由于晶格取代作用和可交换阳离子的解离作用,表面通常带负电,原油由于极性物质的解离作用,表面往往也带负电。在水溶液中,反离子(正电荷)一方面受带电颗粒静电引力作用,规则且紧密地吸附在带电颗粒表面附近,另一方面受热运动的影响而脱离表面,无规则地分散在水溶液中,这便形成了如图2所示的扩散双电层结构[15]。扩散双电层由紧密层和扩散层两部分组成,在紧密层内,电势由表面电势ψ0下降至Stern电势ψδ。在扩散层内,电势则由ψδ下降至零(扩散层边界处)。图2中的红色点划线为滑动面,滑动面上的电势为Zeta电势ζ或动电势,ζ电势是衡量胶体稳定的重要指标。

图2 扩散双电层结构与表面电势分布Fig.2 Electric double layer and surface potential distribution

DLVO理论认为带电胶体粒子以扩散双电层结构存在于溶液中并与其他胶体粒子相互作用。胶体粒子间存在两种相互制约的作用力,一种是范德华引力,它使胶体粒子兼并而聚沉。另一种是扩散双电层重叠所引起的静电斥力,它是维护胶体稳定性的重要因素[16]。其中范德华引力仅是粒子间距的函数,而静电斥力不仅与粒子间距有关,还取决于ζ电势大小。当改变水驱矿化度和离子组成时,易引起ζ电势和静电斥力的变化,从而影响胶体的稳定性[17]。因此研究不同水驱性质下岩石-水膜-原油系统界面ζ电势和界面间相互作用力的变化规律,对于研究水膜稳定性和明确润湿性改变机制的主控因素至关重要。

2 岩石-水膜-原油系统模型

2.1 界面反应物理模型

岩石-水膜-原油系统可视作两个平行且扩散层相互重叠的带电胶体粒子,应用DLVO理论,建立如图3所示的界面反应物理模型,并作出如下假设:

(1)两界面均为无限大的平面,且界面上电荷均匀分布;

(2)初始条件下两界面上均带负电荷且界面间为引力作用;

(3)在扩散层中,正、负离子都视为按Boltzmann分布的点电荷;

(4)介质是通过介电常数影响双电层的,且分散系各处介电常数均相同;

(5)分散系中只有一种对称的电解质,及正、负离子的电荷数均为z;

(6)忽略水驱在水膜中的扩散作用和对油滴冲刷作用。

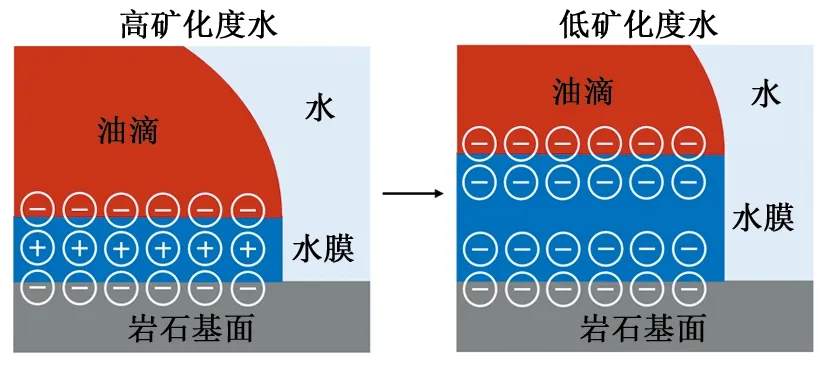
图3 岩石-水膜-原油系统界面反应物理模型Fig.3 Physical model of rock-brine-oil system interface reaction

2.2 分离压力数学模型

当两界面由较远距离逐渐靠近时,界面间产生相互作用力且系统的能量受界面间距的影响,可用分离压力∏表征界面系统单位体积内能量的变化[18-19]:

∏=∏van+∏ele+∏str.

(1)

式中,∏van、∏ele和∏str分别为范德华引力、电斥力和结构力,Pa;∏为界面间的分离压力,Pa。

为了简化计算,现作如下假设:

(1)范德华引力视为负值,静电斥力和结构力视为正值;

(2)范德华引力和结构力不随水驱性质变化而改变。

2.2.1 范德华引力

范德华引力表示两界面间吸附作用的强弱,表达式为

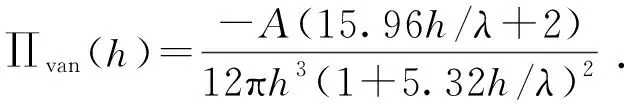
(2)

式中,A为岩石-水膜-原油系统的哈梅克常数,J;λ为London波长,m;h为界面间距,即水膜厚度,m。

哈梅克常数A由真空中两相同物体的实验数据计算而来,这些实验值与公式理论计算相符:

(3)

式中,kB为玻尔兹曼常数,1.38×10-23J/K;ε1,ε2,ε3分别为岩石、水膜和油滴的静态介电常数,F/m;ε1(iv),ε2(iv),ε3(iv)为各介质的电子吸收项;i为第i个电子;v为电子入射频率,Hz;v1为第一个电子的入射频率,Hz;H为普朗克常数,6.626×10-34J·s;T为开氏温度,298.15 K。

原油/二氧化硅在水中的哈梅克常数约为1.0×10-20J。Melrose[20]认为哈梅克常数的范围是0.3～0.9×10-20J。在本文中哈梅克常数取A=0.81×10-20J,London波长取λ=100 nm。

2.2.2 静电斥力

静电斥力由两个相互作用界面上电荷变化引起。电荷可由带电界面电荷的解离或未带电界面电荷的吸附产生,ζ电势是估算双电层静电斥力的重要变量,静电力表达式为

(4)

式中,nb为体积溶液中离子的密度,个/m3;ψr1和ψr2为减小的电势,V;κ为德拜-休克尔双电层厚度的倒数,m-1。

减小的电势ψr1和ψr2表示为

式中,ζi为i界面上的Zeta电势,V;e为电子电荷数,1.60×10-19C。

德拜-休克尔双电层厚度的倒数κ表示为

(5)

式中,NA为阿伏伽德罗常数,6.022×1023;ε0为真空介电常数,8.854×10-12F/m;εr为岩心驱替实验中使用的电解质溶液的相对介电常数,取78.4;z为对称电解质溶液的化合价,对于NaCl溶液,z=1。

2.2.3 结构力

相对于范德华引力和静电斥力这两种长程作用力而言,结构力是作用距离小于5 nm的短程作用力,结构力表达式为

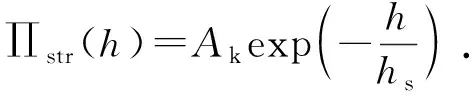
(6)

式中,Ak为结构力系数,Pa;hs为指数模型的特征衰减长度,m。本文中取Ak=1.5×1010Pa,hs=0.05 nm。

3 稳定水膜与岩石润湿性推算

岩石-水膜-原油界面间的分离压力与水膜稳定性密切相连,并最终影响岩石的润湿性。结合Young-Laplace方程和相互作用势能Δω理论[21],可建立分离压力与稳定水膜厚度及润湿角的表征关系,对不同水驱性质下的稳定水膜厚度和岩石润湿性变化形成预测。

3.1 Young-Laplace方程

增广Young-Laplace方程建立了分离压力与曲率、毛管力之间最基本的关系,它通过变分法对图4所示的整个剖面上最小化能量泛函而得来

pc=∏+2Hαγσαγ.

(7)

式中,α为湿相流体;γ为非湿相流体;pc为毛管压力,Pa;Hαγ为表面平均曲率,m-1;σαγ为表面张力(IFT),N/m。

对于图4所示的半月板区域,分离压力∏=0,则公式简化为Young-Laplace方程的一般形式。

图4 圆柱孔道中油水界面与水膜-半月板过渡区轮廓Fig.4 Profile of oil-brine interface in a cylindrical pore and film-meniscus transition zone

对于图5所示的圆柱孔道系统,增广的Young-Laplace方程变形为

(8)

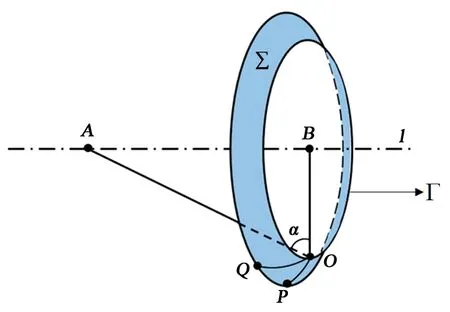
图5 油水界面轮廓曲率半径Fig.5 Curvature of oil-brine interface profile

在区域1中油水界面的曲率1/r1等于角α对于弧长S的变化率:

(9)

右端项可变形为

(10)

(11)

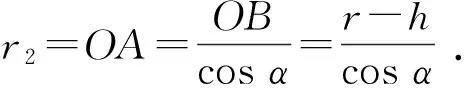
(12)

3.2 相互作用势能Δω理论

当水膜偏离平衡厚度时需要克服两相间相互作用力而做功,引起势能的增加,这种势能在DLVO理论中被称作为“相互作用势能”,记作Δω。相互作用势能Δω描述了两相被第三相分离时势能的变化,是水膜厚度h的函数，即

(13)

式中,Δω为单位区域内的相互作用势能,mJ/m2;heq为水膜平衡厚度,m;∏eq为满足公式(7)的平衡分离压力,Pa。

相互作用势能Δω的几何意义为:水膜由平衡厚度heq变化至任意厚度h时,分离压力曲线∏(h)与平衡分离压力直线y=∏eq围成的面积。以图6(a)为例,直线y=∏eq与分离压力曲线有3个交点,分别为heq1、h3和heq2,其中h3是不稳定平衡点(∂∏/∂h<0)。当水膜厚度由heq2变化至h3时,水膜需要克服正分离压力(斥力)而做功,水膜系统的势能产生等同于正阴影面积的上升。同理当水膜厚度由h3变化至heq1时,负分离压力(引力)对水膜做功,水膜系统的势能产生等同于负阴影面积的下降,heq1和heq2为相互作用势能曲线上两个局部最小值点,对应的相互作用势能变化曲线如图6(b)所示,h3处的峰值称为势垒。当水膜由较大厚度变薄而形成时,由于稳定点heq2,heq1间的势垒作用,水膜优先产生厚度为heq2的亚稳定平衡水膜厚度。

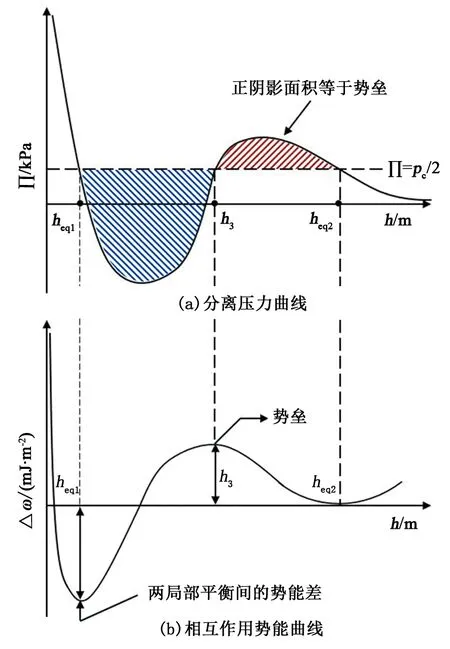
图6 分离压力与相互作用势能对应关系Fig.6 Relations of disjoining pressure and interaction potential

3.3 润湿性表征

在岩石岩-水膜-原油系统中,界面间的相互作用力决定着半月形润湿角。在砂岩油藏的水湿圆柱孔道中,紧贴孔道壁面水膜厚度h和倾斜角α相对于平均孔隙半径r而言是极小量(r≈0,cosα≈1),则

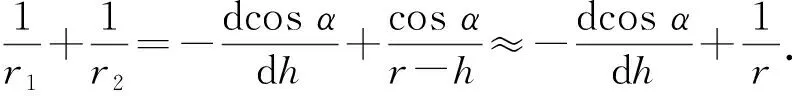
(14)

将式(14)代入到式(8)可得

(15)

以平衡水膜厚度heq为积分下限(α(heq)=0)对公式积分得

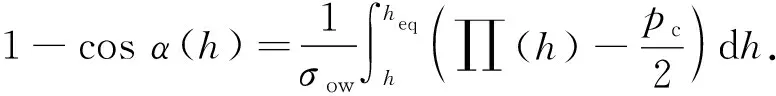
(16)

式(16)的右端项等同于相互作用势能与油水表面张力的比值。从宏观半月形区域(h=h*,∏(h*)=0)处以h*为起点外推至岩石表面即形成了润湿角θw,如图7所示。

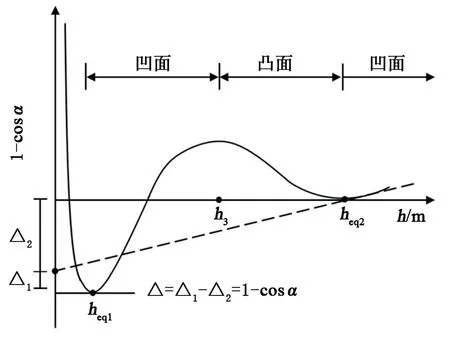
图7 分离压力和倾斜角Fig.7 Dsjoining pressure and angle of inclination

当水膜厚度h>h*,通过对式(16)右端项进行积分变形可得如下线性关系:

(17)

此线性关系直线可以外推至y轴以确定岩石表面的接触角θw,

(18)

4 实例计算及结果分析

4.1 离子价型与矿化度对分离压力的影响

取Nasralla等[22]实验测得的NaCl、CaCl2、MgCl2溶液不同矿化度下油-水界面、岩-水界面ζ电势数据,统计如图8所示。

基于分离压力数学模型和实验数据分别计算一价阳离子NaCl溶液和二价阳离子CaCl2、MgCl2溶液在矿化度为2 g/L下的分离压力曲线,如图9所示。

由图9可知,在矿化度为2 g/L时,NaCl溶液产生正分离压力,界面间为较强的斥力作用,而CaCl2和MgCl2溶液则产生负分离压力,界面间为引力作用。这是由于少量的二价阳离子便可急剧压缩扩散双电层,扩散双电层变薄,同时二价阳离子(反离子)进入紧密层后极大抵消了负电势,ζ电势骤降,界面间静电斥力大幅度减小,最终范德华引力占优。同理,分别计算各溶液在不同矿化度下的分离压力曲线,如图10所示。

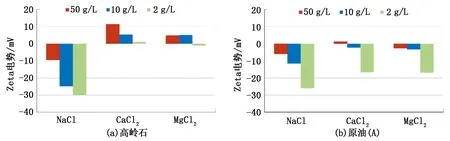
图8 3种溶液不同矿化度下高岭石/水界面与原油(A)-水界面Zeta电势Fig.8 Zeta potential at solid-brine interface for kaolinite and at oil-brine for crude (A) against different concentrations of three solutions

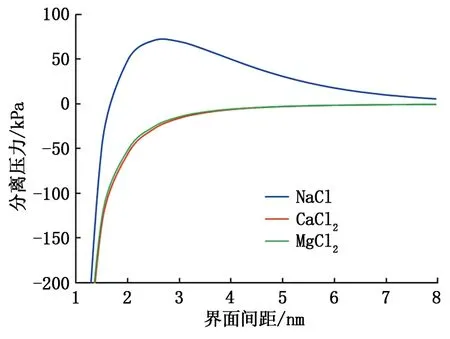
图9 矿化度为2 g/L时各阳离子的分离压力Fig.9 Disjoining pressure with various cation types of 2 g/L

由图10可知,相比CaCl2和MgCl2溶液,NaCl溶液在矿化度高达50 g/L时,界面间的范德华引力才占据优势,分离压力呈现负值。随着NaCl溶液矿化度的降低,阳离子对扩散双电层的压缩作用逐步减弱,双电层膨胀变厚,ζ电势升高,静电斥力增大并占据优势,分离压力随之出现正值。在图10中表现为曲线正峰值逐渐升高,正峰值处的水膜厚度逐渐增大。

由图10还可以看出,CaCl2和MgCl2溶液在矿化度为2 g/L时便可产生负分离压力,且随着矿化度的降低,分离压力曲线基本无变化,界面间仍为引力作用。这充分说明当二价阳离子存在时,矿化度的降低并不能削弱二价阳离子对静电斥力的屏蔽作用,二价阳离子对双电层厚度、ζ电势、静电斥力以及分离压力的影响要远大于矿化度的影响。

综上分析,二价阳离子是控制扩散双电层厚度、ζ电势、静电斥力以及分离压力的主控因素。即使在矿化度极低时,少量二价阳离子便可急剧削弱静电斥力作用,在界面间产生较强的引力,阻碍油滴从岩石表面剥落。

4.2 稳定水膜厚度计算和岩石表面润湿性表征

绘制各溶液在矿化度2 g/L下的分离压力曲线∏(h)与平衡分离圧力直线y=∏eq,如图11(a)。利用相互作用势能Δω理论对各溶液下分离圧力曲线与平衡分离压力之差进行积分求值,绘制如图11(b)所示的相互作用势能曲线。

由图11可知,NaCl溶液在矿化度为2 g/L时存在两个亚稳定水膜厚度heq1与heq2,且这两点间存在较高的势垒。当水膜由较大厚度变薄形成时,由于heq1与heq2点间的势垒作用,优先产生厚度为heq2的稳定水膜,经计算稳定水膜厚度heq=5.334 nm。相同矿化度下CaCl2、MgCl2溶液仅存在一个亚稳定水膜厚度heq1,当水膜由较大距离变薄时,相互作用势能曲线单调递减至heq1,则heq1是唯一的稳定水膜厚度,经计算稳定水膜厚度heq=0.375 nm。综上所述,在相同矿化度下,一价阳离子可产生较厚的稳定水膜,二价阳离子产生较薄的稳定水膜。

联立Young-Laplace方程和相互作用势能Δω理论,计算矿化度为2 g/L时各溶液下的岩石润湿角,如图12所示。

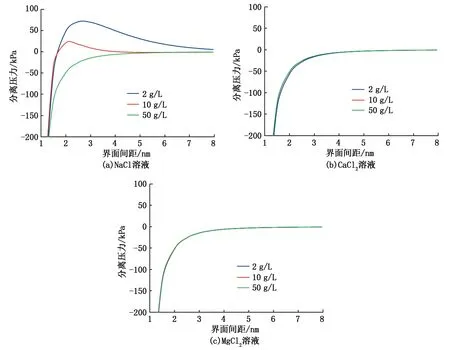
图10 3种溶液在不同矿化度下的分离压力Fig.10 Disjoining pressure with various concentration of three solutions

图11 矿化度为2 g/L时各阳离子的平衡分离压力和相互作用势能Fig.11 Equilibrium disjoining pressure and interaction potential with various cation types of 2 g/L

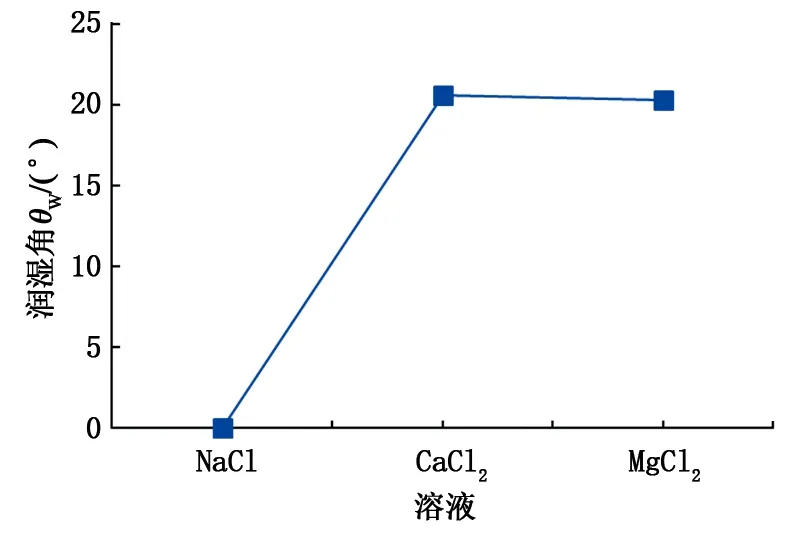
图12 矿化度为2 g/L时各阳离子的岩石润湿角Fig.12 Contact angle of rock with various cation types of 2 g/L

由图12可知,当矿化度为2 g/L时,NaCl溶液下岩石润湿角为0°,CaCl2和MgCl2溶液下岩石润湿角分别为20.55°与20.27°。低矿化度下的一价阳离子溶液能够在界面间产生较强的斥力作用,水膜膨胀变厚,岩石润湿性转变为完全水湿,促使油滴脱离岩石表面,故岩石润湿角为0°。相反,少量的二价阳离子即可产生较强的引力作用,水膜压缩变薄,岩石水湿性减弱,润湿角逐渐增大,不利于原油从岩石表面脱落。

同理做出各溶液在不同矿化度下的相互作用势能曲线(图13),并计算润湿角(图14)。

图13 3种溶液在不同矿化度下的相互作用势能Fig.13 Interaction potential with various concentration of three solutions

图14 3种溶液在不同矿化度下的岩石润湿角Fig.14 Contact angle of rock with various concentration of three solutions

由图13和14可知,随着水驱矿化度的降低,NaCl溶液势垒从无到有,势垒值逐渐升高,稳定水膜厚度逐渐增大,岩石润湿角由20.74°减小至0°,岩石润湿性由水湿变为完全水湿,最终油滴从岩石表面剥落。二价阳离子溶液的相互作用势能曲线基本无变化,水膜始终稳定在较薄的厚度,润湿角维持在20°,不利于油滴脱落和提高洗油效率。

5 结 论

(1)离子价型是影响岩石润湿性的主控因素,少量二价阳离子存在便可急剧压缩扩散双电层,削弱界面间的静电斥力作用,产生负分离压力,形成厚度为0.375 nm极薄水膜,导致岩石水湿性减弱,不利于提高洗油效率。

(2)采用一价阳离子的低矿化度水驱可获得更高的原油采收率。降低水驱矿化度并去除二价阳离子,有利于产生较厚的水膜,使岩石润湿性转变为完全水湿,促使原油脱离岩石表面,洗油效率得以提高。

(3)基于DLVO理论,Young-Laplace方程与相互作用势能理论的分离压力和岩石润湿角计算,可明确岩石润湿性的主控因素,准确预测润湿性的变化,为低矿化度水驱配伍体系优化与砂岩油藏开发潜能评价提供初步的理论基础。