考虑气体多层吸附的表面扩散传输模型

王登科, 李文睿, 浦 海, 魏建平,4, 于 充

(1.河南理工大学河南省瓦斯地质与瓦斯治理重点实验室-省部共建国家重点实验室培育基地,河南焦作454000;2.中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221116;3.河南理工大学安全科学与工程学院,河南焦作 454000; 4.煤炭安全生产河南省协同创新中心,河南焦作 454000)

在煤层气中甲烷含量高达95%～98%[1-3],煤的孔隙具有从埃米到微米尺度的孔径范围,可分为微孔(孔径小于 2 nm),介孔(孔径为2～50 nm)和大孔(孔径大于 50 nm),这些孔径共同构成了煤层的整个孔隙系统[4]。煤体孔隙中气体以游离态和吸附态2种形式存在,且主要以吸附态为主。通常游离气体量和吸附气体量与纳米孔的数量和尺寸密切相关;孔隙数量越多,孔径越小,吸附气体所占的比例就越大[5-6]。由于孔径分布的复杂性,体相气体传输和表面扩散传输共存于多孔介质纳米级孔隙中[7-8]。基于传统的Klinkenberg传输模型[9],研究人员采用引入修正系数的方法提高传输方程的准确性[10-12],但仅是基于连续流方程推导而来。Javadpour等[13-14]引入视渗透率的概念去考虑气体扩散,滑流和气体的吸附解吸效应,认为孔隙中的微流是传统的连续流动与扩散的和。实际上连续流和扩散2种流动机制存在一定耦合关系,不能对2种不同的流动机制进行简单叠加。以线性连续流动假设构建流体传输模型,Freeman等[15]通过尘气模型将扩散流动耦合至连续流的方法对线性流动方程进行修正,但是并未考虑温度的影响。Wang等[16-17]建立考虑渗流-扩散效应的传输模型,但是没有充分考虑表面扩散这一非线性流动机制的影响。纳米孔中存在多扩散系数效应[18]，纳米孔发生表面扩散其表观渗透率预测值比常规水动力学方法预测值高几个数量级[19],显然表面扩散在纳米孔气体传输中占据着重要地位。由于致密页岩中气体自扩散和吸附气表面扩散的相似特性,Miao等[20]利用渗流方程和实验拟合参数,提出一种新的气井产气衰退预测模型,由此说明表面扩散在产气预测方面也具有较大的影响。传统扩散模型认为气体分子扩散是以浓度梯度为驱动力的运移,扩散通量主要与游离态分子浓度相关。与传统扩散模型所不同,吸附气的表面扩散以化学势能梯度为驱动力,与吸附态分子密切相关。Hwang等[21]提出低压条件下的表面扩散模型,并通过实验对其进行验证。基于分子跃迁模型和Langmuir 单层吸附理论,Chen等[22]以单层覆盖度的概念建立理想表面扩散模型。结合分子漫反射边界条件,Wang等[23]提出考虑表面扩散、气体滑移的纳米孔气体传输格子Boltzmann模型。此外,通过耦合体相气体传输机制和吸附气体表面扩散传输机制,吴克柳等[24]还对影响页岩有机纳米孔中气体传输的真实气体效应、应力依赖性和吸附层效应等因素进行分析。然而上述几种模型皆是基于气体分子单层吸附假设建立起来的理论,未考虑多层吸附下的表面扩散传输过程。研究[25]表明,气相混合物在固体表面存在多层吸附现象,表面扩散受吸附层数的影响应予以考虑[26]。由于孔隙内气体吸附量与孔隙压力息息相关,所以压力对于表面扩散的影响不容忽视。随着煤层开采深度的增加,温度的增加也会对表面扩散产生一定影响[27-29]。考虑到甲烷气体在多孔介质里的吸附过程是放热行为,解吸过程是吸热行为,显然温度效应对于超临界吸附下表面扩散传输同样值得深入研究。笔者考虑纳米孔壁面气体多层吸附状态,以多层吸附为理论基础,建立多层吸附表面扩散传输模型,研究温度和压力对表面扩散传输通量的影响效应,以期揭示纳米微孔内非线性扩散气体流动规律。

1 气体传输通道

采用毛细圆管模型代表纳米孔的几何形状(图1(a))。其中圆管内壁面是气体吸附的主要区域,为研究纳米孔中的气体多机制流动机制,选用简化的单圆管作为本文的研究对象。在图1(b)中,圆管半径为r,应力状态下的真实半径为r0,气体吸附层厚度为δ,游离态气体有效运移半径为re。

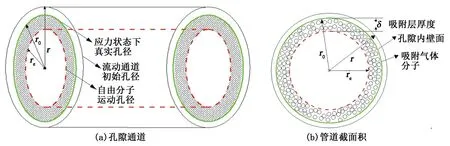
图1 单个纳米圆管简化模型Fig.1 A simplified single nanotube model

不同于大孔径中连续流体的流动机制,在宏观上,孔隙压力引起的变形将直接影响到岩石孔隙率的大小,进而影响整个岩层渗透性。微观上,纳米孔的小变形对孔隙内部气体流动机制、气体吸附传输产生大的影响。根据太沙基有效应力原理,有效应力(pe)等于上覆层压力减去孔隙气体压力:

pe=pover-p.

(1)

式中,pover为围岩上覆层应力,MPa;p为孔隙气体压力,MPa。

同时,对于有效应力下的孔径变化计算式[24]为

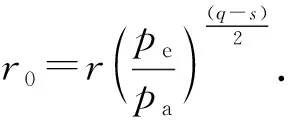
(2)

式中,q为孔隙相关系数常量;s为渗透率相关系数;pa是环境大气压力,0.1 MPa。

在图1(b)中,有效应力下的真实孔隙半径可以表示为

r0=re+δ.

(3)

纳米管中的吸附气体截面积可以表示为

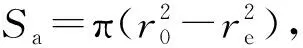
(4)

如果圆管的真实截面积为S=πr02,那么吸附态气体的截面积占圆管总的截面积比例为

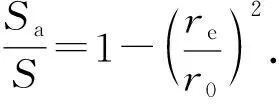
(5)

2 多层吸附理论

2.1 吸附层数

烷烃类气体在多孔介质孔隙内部存在多层吸附现象,吸附层厚度[30]可以表示为

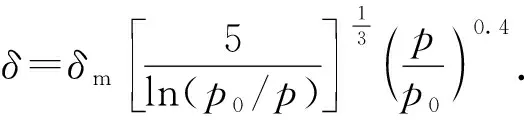
(6)

式中,δm为苯蒸汽单层吸附时的厚度;p0为超临界条件下的甲烷饱和蒸气压。

式(6)由Frenkel-Halsey-Hill吸附理论推导而来,可计算苯蒸汽在多孔介质C-Al2O3内的吸附层厚度。由于苯与铝金属之间发生化学反应,导致单层吸附厚度会发生细微变化。但对于多孔介质煤体中甲烷的物理吸附,其单层吸附厚度等同于吸附气体分子直径,所以δm=0.38 nm。相应的气体吸附层数可表示为

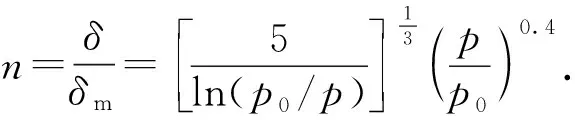
(7)

对于式(7)中超临界吸附条件下的甲烷饱和蒸气压(p0)可采用Dubinin经验公式求解,即

p0=pc(T/Tc)2.

(8)

式中,pc为临界温度下的甲烷饱和蒸气压,4.62×106Pa;Tc为甲烷的临界温度,190.6 K;T为气藏储层温度,K。

由式(7)可知,甲烷吸附层数的变化与温度和压力相关。为研究温度和压力的影响效果,分别计算了吸附层数随压力和温度的变化情况，结果见图2。在图2(a)中,当孔隙压力低于4 MPa时,吸附层数始终处于单层吸附状态,当压力超过4 MPa后吸附层数出现了明显的增加,这与Li的MD分子模拟结果相吻合[31]。同时从图2(b)看出,低压条件下吸附层数受温度的影响非常微弱。但是当压力达到10 MPa后,随着温度的增大吸附层数出现了明显的减少,因此单纯采用Langmuir单层吸附定义壁面上的分子吸附过程是欠准确的。

2.2 传输纠偏因子

多孔介质内部孔隙度直接决定了气体传输的难易程度和流动通道的畅通情况。Dong等[32]通过页岩应力敏感性实验研究,发现有效孔隙度(φe)与初始孔隙度(φ0)、有效应力存在以下关系

φe=φ0(pe/pa)-0.04.

(9)

考虑到纳米孔隙中气体真实传输通道是迂曲的,Wu等[33]引入了体相气体传输纠偏因子,所采用的计算公式为

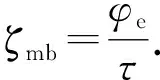
(10)

式中,τ为迂曲度因子,取值4.3。将式(9)代入式(10)可得

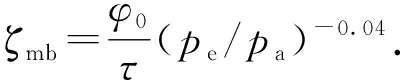
(11)

同样地,对于吸附气的表面扩散也可引入吸附相传输纠偏因子

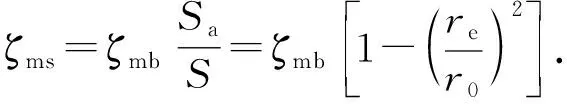
(12)

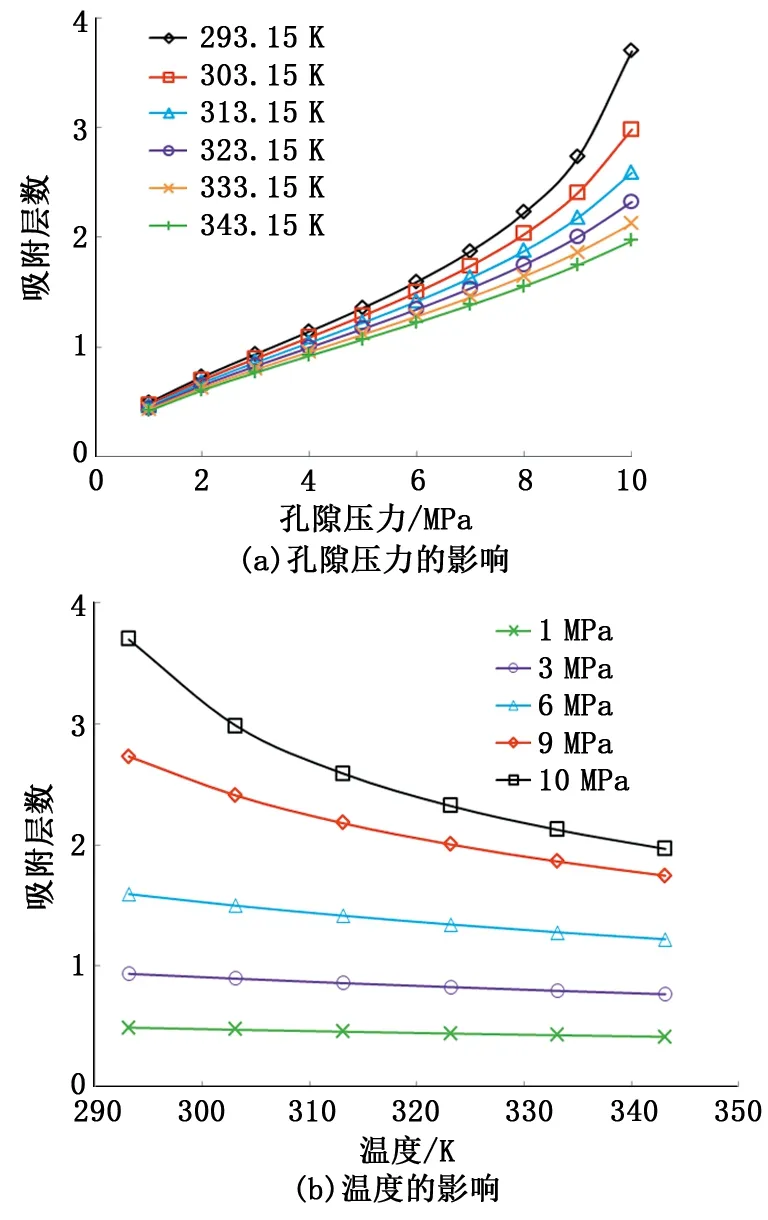
图2 甲烷吸附层数随孔隙压力和温度的变化Fig.2 Variation of adsorption layers with pressure and temperature for methane molecules

2.3 多层吸附表面扩散模型

表面扩散是多孔介质固体表面吸附气体在化学势能梯度作用下,产生的一种运移传输现象(图3)。理论研究表明,当孔径小于2 nm时,表面扩散的传输贡献率高达90%[34]。假设纳米孔中体相气体与吸附相气体存在动态平衡,通过公式推导可将表面扩散通量转化为与浓度梯度相关的表达式[35]，即

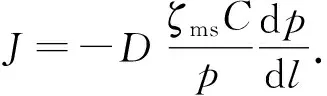
(13)

式中,D为表面扩散系数,m2/s;C为纳米孔壁面吸附气体质量浓度,kg/m3。

为了得到式(13)中的表面扩散系数D,郭亮等[36]在进行超临界温度下的甲烷-纳米活性炭吸附实验后,给出以下经验表达式：

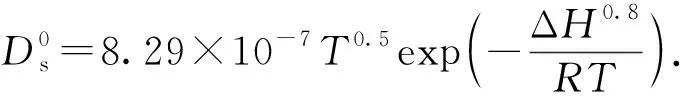
(14)

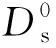
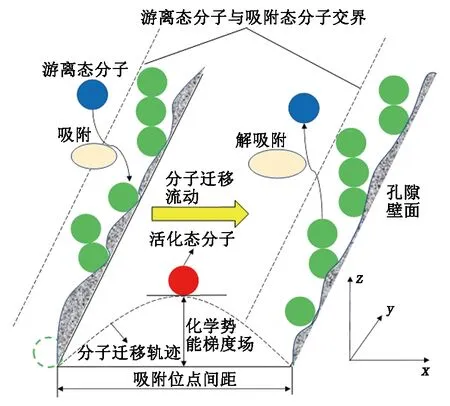
图3 分子多层吸附的表面扩散传输行为Fig.3 Transport behavior of surface diffusion for molecular multi-layer adsorption

通常,高压条件下的新型表面扩散模型中[34]的 ΔH是一常数,本文中对甲烷超临界吸附条件下的等量吸附热与吸附量实测数据[38]进行拟合计算,得出了更加可靠的ΔH计算表达式：

ΔH=-3.44lnυ+16.365.

(15)

式中,υ为修正的吸附量,m3/kg。

煤体中的甲烷吸附量受煤岩成分、温度和压力等因素影响,利用 Langmuir 等温吸附模型可以很好地计算出多孔介质内部低压条件下的气体吸附量,但是Langmuir 等温吸附模型在估算超临界条件下的气体吸附量时会导致较大的理论偏差[39]。

为准确计算不同温度和压力环境下的甲烷吸附量,利用超临界条件下吸附层数计算可得

υ=nυm,

(16)

其中

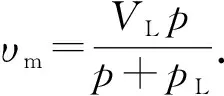
(17)

式中,υm为理想气体单层吸附量,m3/kg;VL为Langmuir气体体积,m3/kg;pL为Langmuir 压力,MPa。通常来说,VL和pL可通过实验测量结果得出,对于甲烷超临界吸附情况下,可采用表1实验所测数据[40]。

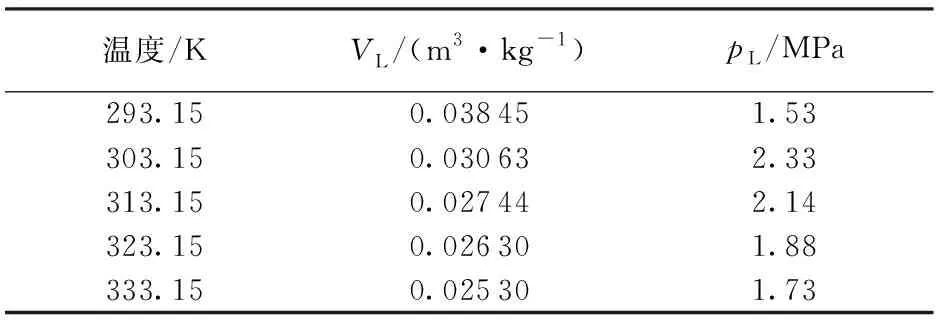
表1 中级煤的Langmuir压力与Langmuir体积

由于经验表达式(14)并未考虑压力的影响,基于单层吸附假设,Chen等[41]通过引入不同压力下气体吸附覆盖度的概念,提出以动力学的方法计算表面扩散系数的表达式

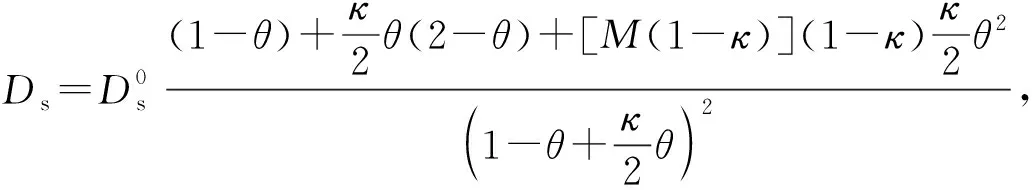
(18)

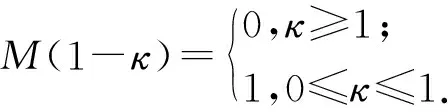
(19)

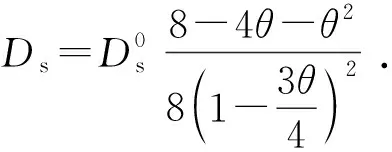
(20)

对于Langmuir单层吸附而言,以分子覆盖理念推导而来的吸附气体浓度[24]可表示为

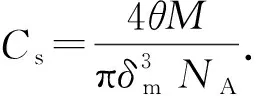
(21)

式中,NA是阿伏伽德罗常数,6.02×1023, 1/mol。将式(20)和式(21)代入式(13),可得单层吸附模型假设下的表面扩散通量为

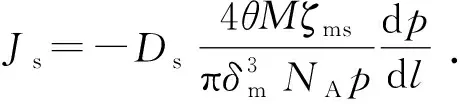
(22)

对于多层吸附模型的表面扩散系数求解,以单层吸附理论为基础的表面扩散系数计算式为

(23)

式中,「n⎤为对数值n向上取整数,无量纲。相应地,多层吸附的吸附气浓度可以表示为

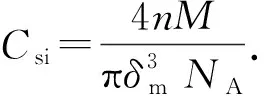
(24)

将式(23)和(24)代入式(13)可得多层吸附模型的表面扩散通量表达式:

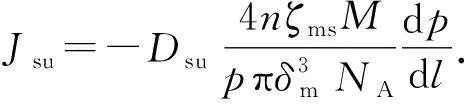
(25)

3 模型验证

3.1 表面扩散系数验证

通过实验手段对纳米孔中的表面扩散通量进行验证难以实现,目前也尚未有相关数据发表出来,因此不能通过实验手段直接对本文中模型进行直接验证。但可以首先通过理论计算验证表面扩散系数的合理性,其次计算表面扩散通量与单层吸附表面扩散通量作对比,间接验证模型的合理性。对吸附气表面扩散系数的验证,图4中给出了特定压力范围内单层吸附公式(20)计算得到的理论数据、本文中提出的多层吸附公式(23)计算得到的表面扩散系数和若干实验测试数据。此外,还将已发表文献中的相关实验数据与理论计算取值进行了归纳总结,结果见表2。

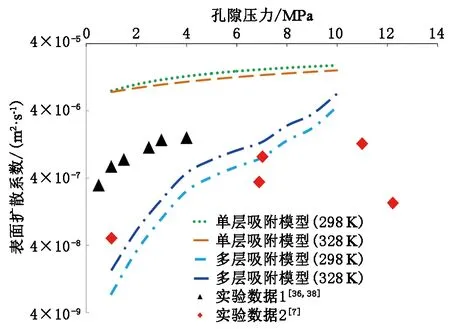
图4 表面扩散系数的理论计算结果与实验数据比较Fig.4 Comparison between theoretical data and experimental data of surface diffusion coefficient

由图4比较发现,与单层吸附假设计算得到的表面扩散系数相比,本文中提出的多层吸附模型所计算得到的表面扩散系数与实验数据比较接近。从表2中所列详细的相关数据也可以看出,本文中提出的多层吸附表面扩散系数计算结果的数量级区间(10-9～10-6m2/s)也更为准确。此外,在全压力(1～10 MPa)范围内,利用单层吸附模型所计算得到的表面扩散系数很明显远大于本文中多层吸附模型的计算结果,尤其是在低压力情况下(小于4 MPa)表面扩散系数就达到了10-5m2/s的数量级,与相关实验数据[46]有着将近3个数量级误差,很明显单层吸附模型的计算结果失真了。由于压力的增加气体吸附量增大,2种模型的计算数值都出现了不同程度的增大,但是单层吸附模型的表面扩散系数始终没有出现跨数量级的增加,与实际情况不相符。同时,由于单层吸附模型中假定等量吸附热ΔH是不随温度变化的[32],计算结果显示,温度升高表面扩散系数并未增大,而是出现了减小,这也不符合实际。综上所述,本文中基于多层吸附模型提出的表面扩散系数计算方法更为合理、准确。

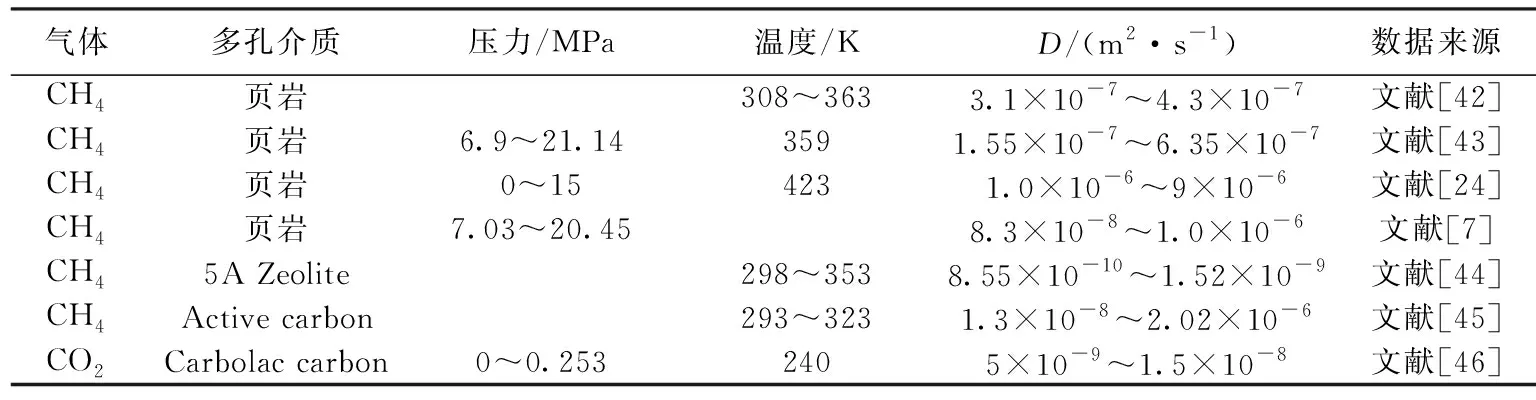
表2 表面扩散系数值

3.2 表面扩散通量验证

由于表面扩散通量无法通过实验测得,所以选择合适的表面扩散系数计算表面扩散通量就尤为重要。根据式(22)和(25)分别计算出单层吸附和多层吸附的表面扩散通量,对比结果如图5所示。

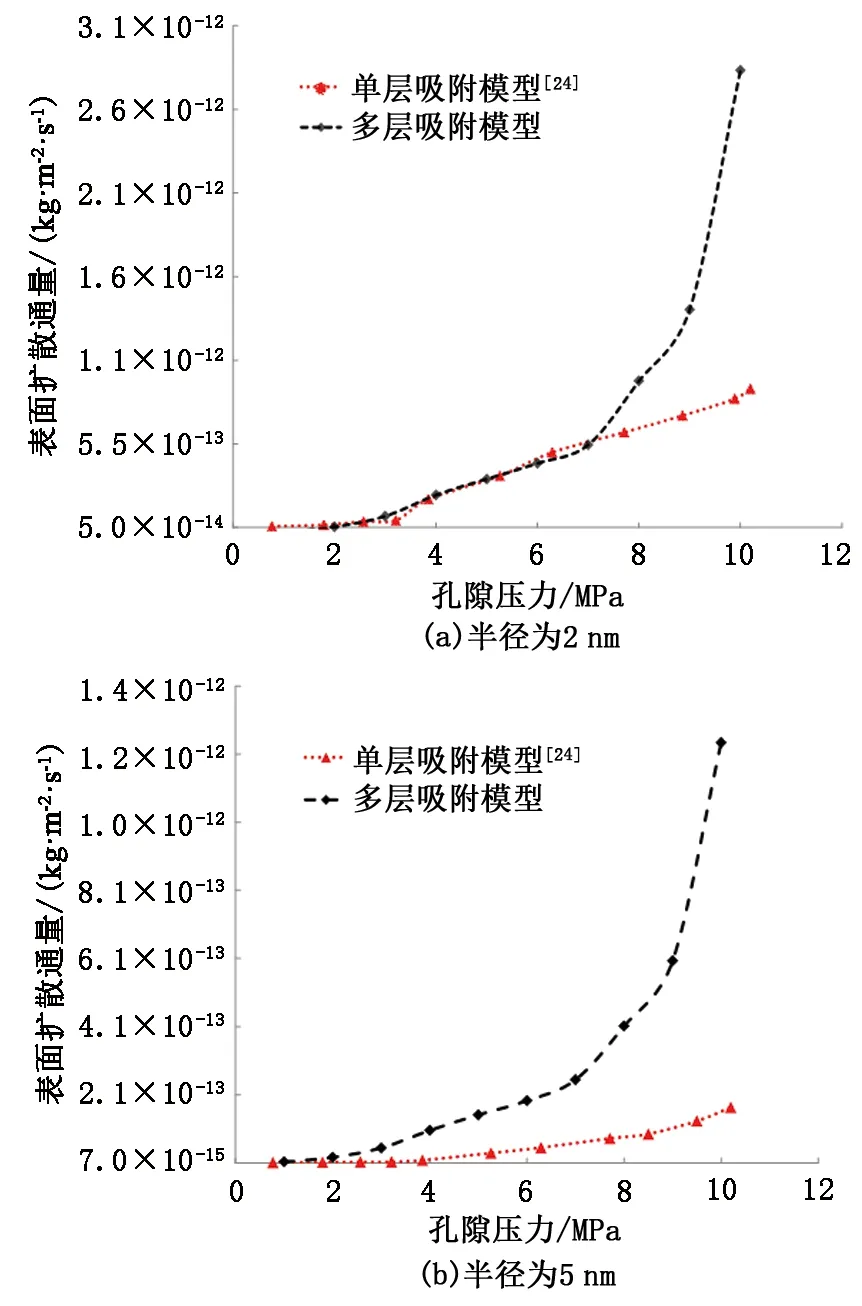
图5 单层吸附模型[36]与多层吸附模型表面扩散通量理论数值对比Fig.5 Comparison of theoretical prediction between monolayer adsorption model[36] with multilayer adsorption model

其中温度为423 K,孔隙压力取1～10 MPa。

通过式(22)和(25)的计算结果比较,在图5(a)中,可看到在压力小于7 MPa情况下,单层吸附表面扩散通量与本文中的多层吸附表面扩散通量计算结果吻合很好,但是压力持续增大后,多层吸附的表面扩散通量明显大于单层吸附的表面扩散通量。另外,从图5(b)中看到,在半径为5 nm孔隙中,2种吸附模型计算得出的扩散通量存在较大差异,单层吸附的表面扩散通量明显小于多层吸附表面扩散通量,且随着压力的增大二者差值越来越大,当压力达到10 MPa时,两者计算结果差值达到了一个数量级。随着压力的增大,2种吸附模型计算得出的扩散通量差值越来越大的原因在于，在多孔介质没有达到气体吸附饱和情况下,压力的持续性增大导致吸附量呈现出非线性的增大趋势,再辅之以高浓度梯度驱动力,导致表面扩散通量出现明显增大。因此,多层吸附表面模型在计算表面扩散通量方面是可行的。同时,通过图5也可以发现,2 nm孔隙内部表面扩散通量是5 nm孔隙内部表面扩散通量的2～3倍,说明表面扩散通量对纳米孔径也具有明显的依赖性。

4 压力和温度对表面扩散传输的影响

为研究压力对表面扩散传输机制的影响,以温度为298 K,孔隙半径为2和5 nm分别作为研究对象,压力区间范围是1～10 MPa,结果如图6(a)所示。关于温度对表面扩散传输机制的影响,这里以2 nm半径的孔隙作为研究对象,压力取值为3、6和9 MPa,温度范围为293～333 K,结果如图6(b)所示。

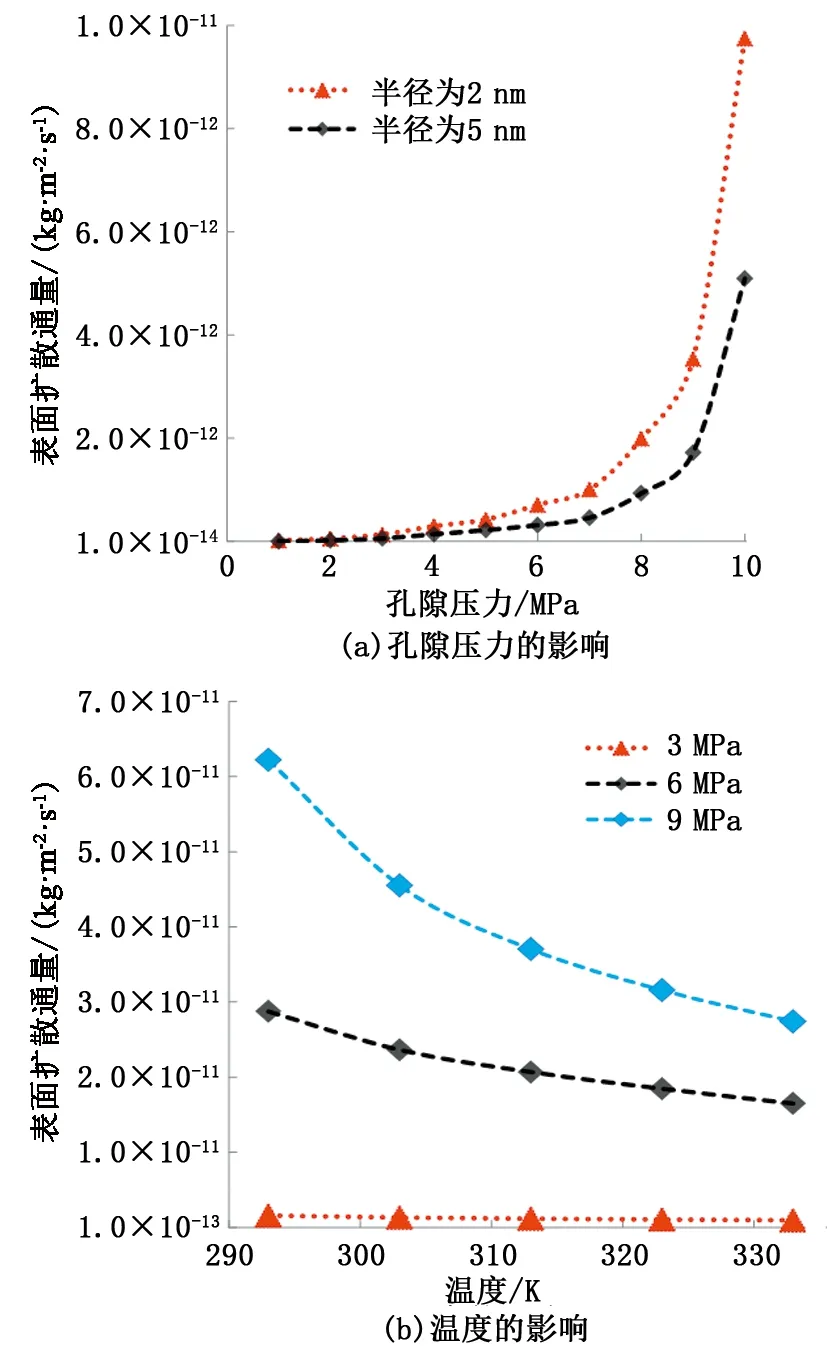
图6 孔隙压力和温度对表面扩散通量的影响Fig.6 Effect of nanopore pressure and temperature on surface diffusion flux

从图6(a)看出,当压力从1 MPa增至10 MPa过程中,表面扩散通量随着压力的增大而增大,呈现出指数式增长。经过计算,在同一孔径内部,高压10 MPa下的表面扩散通量比低压1 MPa下的表面扩散通量大了将近两个数量级。其原因为，同一孔隙内部,由于孔隙压力的增加导致气体吸附量明显增大,因而壁面吸附分子浓度增大加之对扩散粒子起到驱动力的高压力梯度,导致表面扩散通量显著增大。同时计算发现,在以表面扩散传输为主导的2 nm孔隙内部,其表面扩散通量是5 nm孔中的2倍。

从图6(b)可以看出,随着温度的增加,表面扩散通量呈现缓慢降低趋势,说明温度的升高阻碍了表面扩散传输。经过计算,当温度从293 K增大到333 K后,在3 MPa压力下,表面扩散的传输通量下降了37.40%;在6 MPa压力下,表面扩散的传输通量下降了42.47%;在9 MPa压力下,表面扩散的传输通量下降了55.84%,平均下降约为45.24%。其原因为，温度升高加速了纳米孔吸附气的解吸,导致孔隙壁面气体吸附量减少,表面扩散系数虽有所增加，但远小于吸附气体浓度的降低幅度,最终导致了表面扩散通出现减少趋势。

5 结 论

(1)相对于根据Langmuir单层吸附假设所建立的气体表面扩散系数计算公式,在耦合等量吸附热与吸附量的变化关系后,基于多层吸附理论所建立起来的吸附气体表面扩散系数计算公式在描述气体表面吸附方面更加合理、准确。

(2)基于多层吸附理论所建立起来的吸附气体表面扩散新模型比以Langmuir单层吸附假设所建立的传统吸附气体表面扩散模型更具普适性,耦合了温度与压力效应之后的纳米孔吸附气体表面扩散模型不仅适用于低温低压条件,而且适用于高温高压的超临界条件,更加准确全面地反映了吸附气体的表面扩散传输机制。

(3)在未达到吸附平衡之前,吸附气体表面扩散通量随压力的增加而增大,呈现出类指数式增长;恒温条件下,压力升高后,受气体吸附量明显增加的影响,吸附气体表面扩散通量增加显著。吸附气体表面扩散通量随温度的升高而降低,降幅较为缓慢,温度的升高强化了孔隙表面的气体解吸,弱化了气体表面扩散效应。