形式背景的下近似协调与粒协调的关系

陈东晓， 李进金，2

(1. 华侨大学 数学科学学院， 福建 泉州 362021；2. 闽南师范大学 数学科学与统计学院， 福建 漳州 363000)

形式概念分析(FCA)是由德国数学家Wille[1]提出的一种分析数据的有效工具，它的核心是形式背景和概念格.形式背景是由对象集、属性集以及对象和属性之间的二元关系构成的.而概念格是将形式背景里的对象子集和属性子集以一种概念层次体现出来.近年来，形式概念分析已被广泛应用于概念认知、知识提取等领域.形式背景是形式概念分析中数据的组织形式，由对象集、属性集与两者之间的一个二元关系组成.形式背景中有3种基本的模态逻辑算子，即充分性算子、必要性算子和可能性算子[2].Wille利用充分性算子,建立起对象幂集和属性幂集间的一个伽罗瓦连接,给出了形式概念的定义.一个形式背景中,所有形式概念构成一个完备格，称为概念格.因此，形式概念分析也被称为概念格理论.必要性算子和可能性算子分别就是粗糙集理论[3]中的下近似算子和上近似算子.利用上、下近似算子,Yao[4]给出了对象定向概念格的定义，Gediga等[2]定义了属性定向概念.通过对照形式概念的研究，对象定向概念格和属性定向概念格也取得了许多研究结果.Shao等[5]研究了对应的属性约简问题， 给出了约简的算法.形式背景上的模态逻辑算子在一定意义下可以相互转换，这为概念格理论与粗糙集理论之间建立起“沟通”的桥梁.因此，在形式背景中，粗糙集理论与概念格理论具有非常密切的联系.形式背景中粗糙集近似本质上是广义近似空间中的粗糙运算，它的一个特点是近似集和被近似集不在同一论域.粗糙集理论的一个主要应用是提取决策规则，它要求近似集和被近似集必须在同一论域.为了在形式背景中利用粗糙集方法导出决策规则，Li等[6-7]在形式背景中给出了几种修正的粗糙近似，针对其中一种粗糙近似运算研究了基于决策规则的属性约简问题.Dempser-Shafer 证据理论以基本概率分配为基础，利用信任函数和似然函数构成的不确定区间刻画证据的不确定性和未知性.集合的信任测度和似然测度可以看成是对该集合的不确定性的定量刻画，而同一集合的上近似和下近似可以看成是对该集合所表示信息的定性描述，那么证据理论与粗糙集理论之间存在必然的联系[8-10].文献[11-17]研究了利用证据理论刻画信息系统、决策信息系统中的属性约简问题,文献[18-22]分别通过建立一对覆盖近似算子与信任函数、似然函数的联系以讨论覆盖决策信息系统的约简.在形式背景中，概念格理论与粗糙近似理论之间有着密切关系[23]，同样可以利用证据理论刻画形式背景的属性约简问题.本文给出形式背景下的一种粗糙近似集定义，通过定义信任函数和似然函数，给出下近似协调集的等价结论，讨论了下近似协调集的约简，定义了上、下近似核心属性，并给出充要条件.最后，定义了下近似协调的决策形式背景，并得到决策形式背景的下近似协调与粒协调是等价的.

1 基本概念和定理

定义1[1,24]形式背景(U，A，I)，其中,U为对象集，A为属性集，I为U与A之间的二元关系，(x，a)∈I，表示对象x具有属性a，也记为xIa.

设X⊆U，B⊆A，定义在形式背景(U，A，I)上的算子,即

X*={a∈A|∀x∈X，xIa}，B*={x∈U|∀a∈B，xIa}.

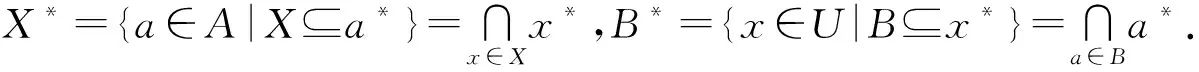
命题1[24]设(U，A，I)为一个形式背景，∀x∈U，a∈A,则有x**=(x)A=∩{X|x∈X，

X∈LU(U，A，I)}，a**=(a)U=∩{B|a∈B，B∈LA(U，A，I)}.

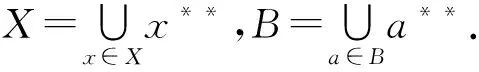
利用粗糙集理论中的上、下近似算子的定义，引入定义2.

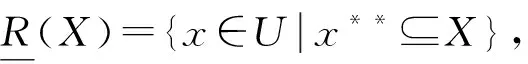
根据定义2有如下结论.

定理1设(U，A，I)为一个形式背景，∀X⊆U，Y⊆U，则有如下结论:

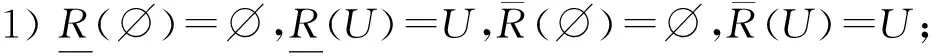
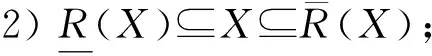
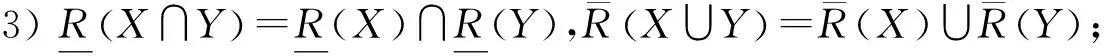
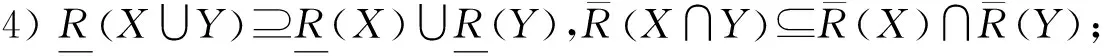
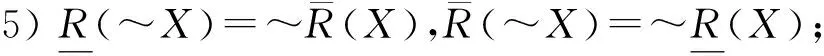
证明：容易直接根据定义2证得.

∀B⊆A，定义X*B={a∈B|∀x∈X，xIa}，C*B={x∈U|∀a∈C，xIa}，其中，X⊆U，C⊆B,容易得到X*B=X*∩B，且有X*A=X*.

命题3[3]设(U，A，I)为一个形式背景，C⊆B⊆A,则∀X⊆U，∀x∈U,有

1)X*C⊆X*B⊆X*A，x*C⊆x*B⊆x*A；

2)X*A*A⊆X*B*B⊆X*C*C，x*A*A⊆x*B*B⊆x*C*C；

3)C*B=C*A.

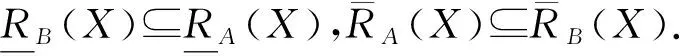
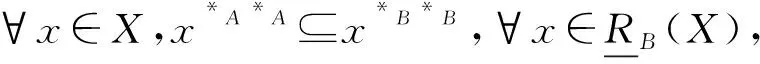
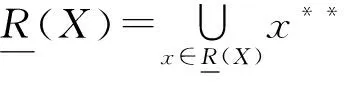
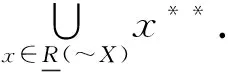
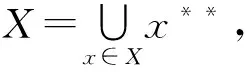
2 形式背景的上、下近似协调集

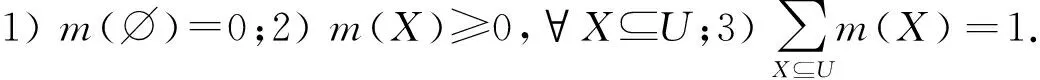
若m(X)>0，称X是m的焦元，记M={X⊆U|m(X)>0}，序对(M，m)为U上的一个信任结构.

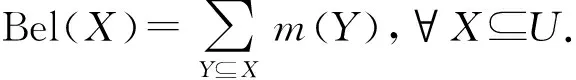
同一信任结构导出的信任函数和似然函数对偶，即Pl(X)=1-Bel(～X)，且Bel(X)≤Pl(X).

粗糙集理论和Dempster-Shafer证据理论之间有很强的联系.以下定理4表明，经典的信念和似然函数可以用Pawlaks集合的上、下近似来表示.

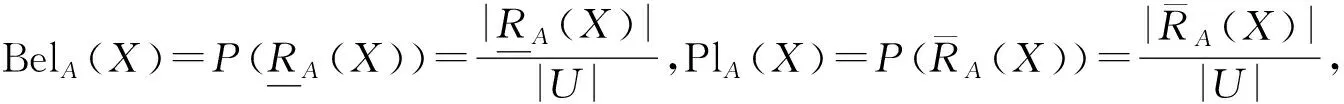
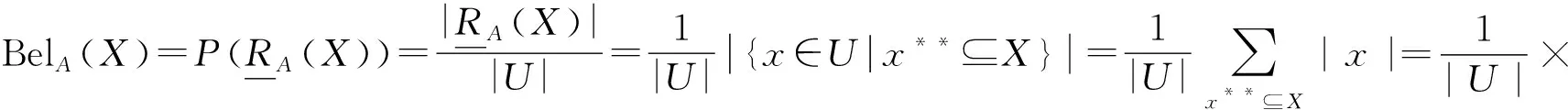
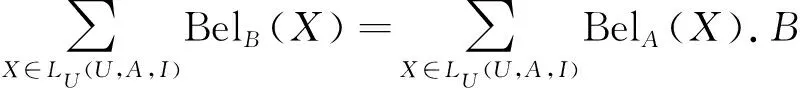
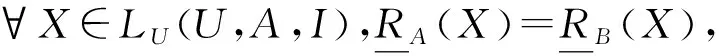
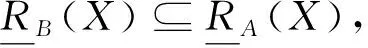
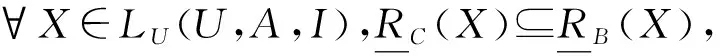
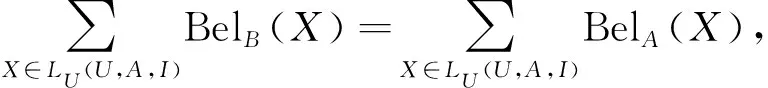
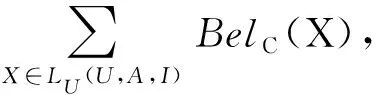
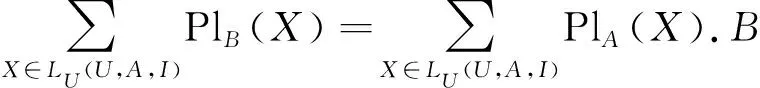
证明:与定理5证明类似.

定义6[24]设(U，A，I)为一个形式背景，B⊆A，若∀x∈U，x*B*B=x*A*A，则称B是(U，A，I)的粒协调集.

定理7设(U，A，I)为一个形式背景，B⊆A，则B为下近似协调集当且仅当B为粒协调集.

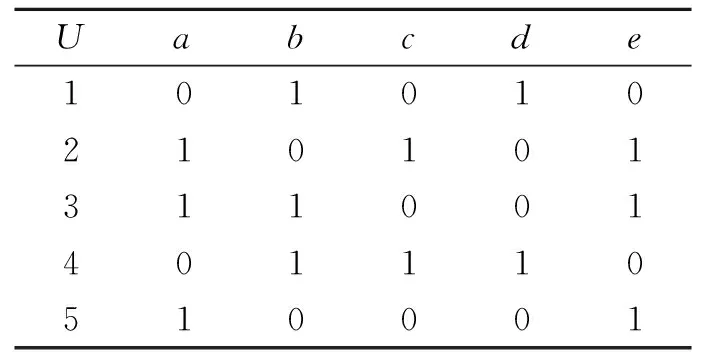
表1 形式背景(U，A，I)Tab.1 Formal context (U,A,I)

x*B*B，B是(U，A，I)的粒协调集.

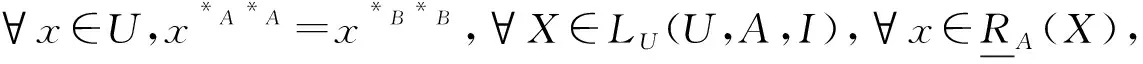
例1设(U，A，I)为一个形式背景，U={1，2，3，4，5}，A={a，b，c，d，e}.形式背景,如表1所示.

该形式背景中，对应的形式概念为L(U，A，I)={(U，∅)，(134，b)，(235，ae)，(24，c)，(14，bd)，(3，abd)，(2，ace)，(4，bcd)，(∅，A)}.取B={a，b，c，d}，验证得

即B是下近似协调集.由文献[24]容易验证B是粒协调集.

3 决策形式背景的上、下近似协调集

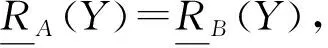
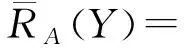
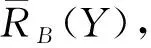
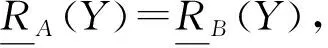
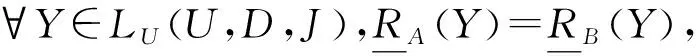
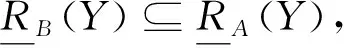
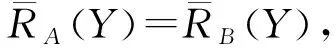
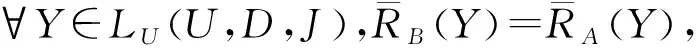
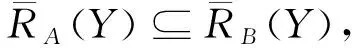
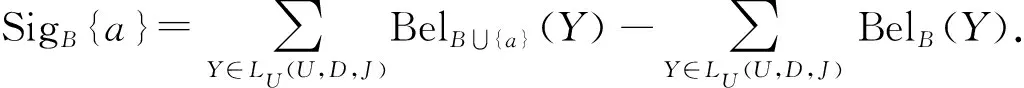
定理10CoreL(A，D)={a∈A|SigA{a}{a}>0}.

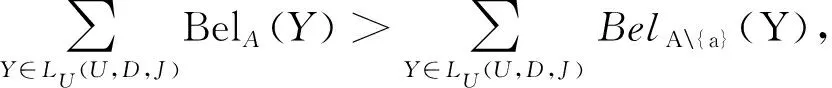
同理，可以定义上近似协调下的属性重要度.

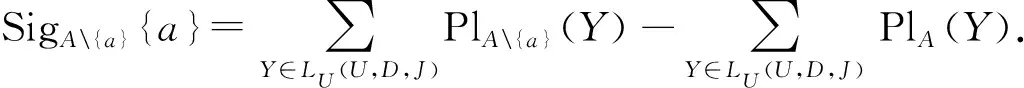
定义12假设(U，A，I，D，J)为一个决策形式背景，B⊆A，a∈AB对于B的重要度为SigB{a}=

表2 决策形式背景(U，A，I，D，J)Tab.2 Decision formal context (U,A,I,D,J)

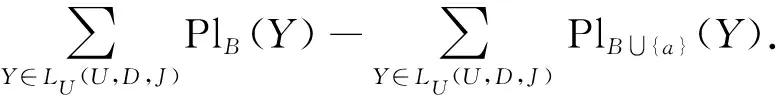
定理11CoreU(A，D)={a∈A|SigA{a}{a}>0}.

证明:类似定理10证明.

例2设(U，A，I，D，J)为一个决策形式背景，U={1，2，3，4，5}，条件属性A={a，b，c，d，e}，决策属性D={f，g，h}.该决策形式背景,如表2所示.

在此决策形式背景中，条件属性对应的概念格为L(U，A，I)={(U，∅)，(134，b)，(235，ae)，(24，c)，(14，bd)，(3，abd)，(2，ace)，(4，bcd)，(∅，A)}.决策属性对应的概念格为L(U，D，J)={(U，∅)，(14，f)，(235，g)，(2，gh)，(∅，D)}.计算得B1={a，c，d}和B2={c，d，e}是其两个下近似约简集，其下近似核心属性为CoreL(A，D)={c，d}.

4 决策形式背景的下近似协调与粒协调的关系

定义13[24]设(U，A，I，D，J)为一个决策形式背景，如果∀x∈U，有x*A*A⊆x*D*D，则称(U，A，I，D，J)为协调的;否则,称(U，A，I，D，J)是不协调的.

定理12设(U，A，I，D，J)为一个决策形式背景，(U，A，I，D，J)是粒协调的，当且仅当(U，A，I，D，J)是下近似协调的.

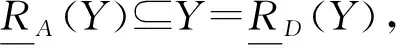
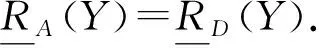
Li等[25]介绍了粒协调与强协调及弱协调之间关系，三者相互不一样,而文中定义的下近似协调与粒协调等价，这里不再一一介绍三者之间的关系.

5 结束语