大尺寸条石无浆砌缝力学性能试验

江云帆， 郭子雄，2， 许秀林

(1. 华侨大学 土木工程学院， 福建 厦门 361021；2. 华侨大学 福建省结构工程与防灾重点实验室， 福建 厦门 361021)

石结构建筑因质朴美观、耐久性好等特点而广泛分布于世界各地.其中，大量古石建筑采用的砌筑形式为无浆砌筑(砌块间未使用胶结材料)，如西班牙古罗马大渡槽、柬埔寨古高棉帝国庙宇、非洲大津巴布韦遗址、秘鲁印加遗址、欧洲南部地区的中世纪修道院[1]和中国河南省的铁佛寺石村等.此外，许多历史老旧建筑的砌筑砂浆因长年遭受物理及化学侵蚀而大量脱落，导致其砌缝力学性能与无浆砌筑十分类似.为了更好地保护这些古石建筑，合理评估其抗震性能并提出相应的修复加固措施，有必要对无浆砌筑石结构的受力性能进行研究.目前，国内外学者主要针对有浆砌筑石墙的力学性能开展研究[2-6]，而对无浆砌筑石墙力学性能的研究仍不系统.Lourenço等[7-8]对西班牙加泰罗尼亚地区无浆砌筑砂岩建筑的抗震性能进行研究，通过拟静力试验研究砌缝和石墙的滞回性能；Vasconcelos等[9-10]对不同竖向压应力下，花岗岩无浆砌缝及石墙的滞回性能进行研究，并根据试验结果提出石墙极限承载力的简化计算方法；文献[11-12]对42片缩尺大理石无浆砌筑石墙进行静力试验，主要研究墙体长度、窗洞位置、横纵墙连接强度、竖向荷载和楼层数对墙体倒塌机制的影响，并提出能准确预测墙体倒塌机制的分析计算模型；Bui等[1]通过有限元模拟，证明离散元法(DEM)能准确模拟无浆砌筑墙体平面内和平面外的力学行为；文献[13-15]研究了岩石界面的摩擦性能；文献[16-21]提出不同的岩石界面剪切强度准则.这些研究对深入了解无浆砌筑石结构砌缝力学性能有一定的参考价值.目前，在无浆砌缝力学性能的试验中采用的石材尺寸较小，不能反映实际结构中砌缝的尺寸.因此，本文对大尺寸花岗岩条石无浆砌缝的力学性能进行研究.

1 试验概况

1.1 试件设计制作

(a) 试件实物 (b) 试件尺寸图1 试件特征(单位：mm)Fig.1 Details of specimens (unit： mm)

无浆砌筑双剪试件由3块界面形式相同的花岗岩条石无浆叠砌而成.上、下皮条石尺寸(长×宽×高)均为590 mm×200 mm×200 mm，中间皮条石尺寸(长×宽×高)为800 mm×200 mm×200 mm.试件特征，如图1所示.

试验研究参数为砌缝界面形式和竖向压应力.界面形式包括机器切割面(下文简称机切面)，通过机器随机锤击机切面而成的荔枝面和通过对机切面进行抛光处理而成的抛光面.石材界面特征，如图2所示.竖向压应力采用0.2，0.4，0.6 MPa三种水平.试件共有10个，试验参数及主要试验结果，如表1所示.表1中:σ为竖向压应力；μs为静摩擦系数.

(a) 机切面 (b) 抛光面 (c) 荔枝面图2 石材界面特征Fig.2 Characteristics of stone interfaces

表1 试验参数及主要试验结果
Tab.1 Test parameters and main test results

试件编号界面类型σ/MPaμs试件编号界面类型σ/MPaμsMC-1机器切割0.20.77P-2抛光0.40.61MC-2机器切割0.40.66P-3抛光0.60.71MC-3机器切割0.40.74BH-1荔枝0.20.76MC-4机器切割0.60.67BH-2荔枝0.40.66P-1抛光0.20.76BH-3荔枝0.60.59

图3 双灰缝剪切试验装置Fig.3 Double-joints test setup

1.2 试验装置和加载制度

欧洲规范[22]中规定，研究砌体水平灰缝平面内初始抗剪强度时，应采用双灰缝剪切试验装置，如图3所示.图3中：F为荷载；Fn为垂直于灰缝的荷载.试验采用华侨大学课题组研发的双灰缝剪切试验装置加载，加载装置如图4所示.为减少上、下压板摩擦力对理想剪切试件边界条件的不利影响，在上、下压板上安装低摩阻滚轴.为了防止试件在加载过程中发生平面外的偏移，在中间皮条石及水平作动器两侧设有侧向限位滚轴.

竖向荷载由竖向液压伺服作动器施加，通过上压钢垫板均匀施加于试件上表面，其大小根据试件正应力水平确定，并在加载过程中保持恒定.水平荷载通过水平液压伺服作动器施加于中间皮条石.水平加载采用位移控制.MC-3试件按20 mm和40 mm的位移幅值加载，各幅值循环5次；其余9个试件在40 mm位移幅值下循环加载10次，加载速度为0.5 mm·s-1.

(a) 示意图 (b) 实物图图4 加载装置Fig.4 Test setup

1.3 量测方案

图5 位移计的布置Fig.5 Arrangement of displacement meters

试验测量的数据包括竖向荷载、水平荷载和条石界面水平位移.水平和竖向荷载通过作动器的拉压传感器测量.条石水平位移等于中间皮条石相对于上、下皮条石支座的水平位移.中间皮条石水平位移通过布置于料石两侧的激光位移计(LDT)测量.支座位移通过布置于上、下皮料石侧面的电子位移计(LVDT)监测.位移计的布置，如图5所示.试验数据经由DH3816N型数据采集仪和计算机等设备在加载过程中全程采集并记录保存.

2 结果及分析

2.1 界面损伤特征及分析

(a) 机切面

(b) 抛光面 (c) 荔枝面图6 界面损伤特征Fig.6 Damage details of interfaces

界面损伤特征，如图6所示.由图6(a)，(b)可知：机切面及抛光面加载结束时，局部均产生了若干条状划痕.这是因为受加工技术精度的限制，机切面和抛光面难以保证完全平整，界面间为局部接触.压剪作用下，由于局部接触面压应力较大，石材中的硬质矿物晶粒嵌入软质石材表面并往复犁削，类似于摩擦学中的“犁沟效应”，进而产生划痕.

由图6(c)可知：荔枝面循环加载过程中产生了大量石粉，加载结束时,界面产生了整体磨损.这是由于界面微凸体尺寸较小，强度较低，往复摩擦过程中其局部不平整接触面被磨蚀，界面随后进入整体摩擦状态.

2.2 单向加载特性

图7 第一循环荷载-位移骨架曲线Fig.7 Load-displacement skeleton curves in first loading cycle

2.2.1 荷载-位移曲线 不同界面试件的第一循环荷载-位移骨架曲线，如图7所示.图7中：Δ为位移；Fw为初磨损荷载；Fs为静摩擦力.

由图7可知:曲线形状与小尺寸界面[9]基本一致;加载初期，曲线均基本为直线，砌缝处于弹性阶段；超过初磨损荷载Fw后，砌缝进入界面磨损阶段，此时，由于界面磨损，砌缝刚度逐渐减小；超过静摩擦力Fs后，砌缝进入滑动摩擦阶段，此后，随位移的增加，砌缝荷载仅略有变化.

2.2.2 静摩擦系数 由于加载初期试验采集数据点较少，所测得的砌缝初磨损荷载值不准确，故仅对砌缝的静摩擦系数进行讨论.静摩擦系数等于静摩擦力与竖向压力的比值，不同界面试件的静摩擦系数，如表1所示.

由表1可知:1) 在竖向压应力为0.2,0.4 MPa下，3种界面的静摩擦系数近似相等，这主要是因为类“犁沟效应”产生的犁削力增加了机切界面及抛光界面间的抵抗力；2) 随竖向压应力的增加，各界面静摩擦系数的变化无明显规律，机切面及抛光面的静摩擦系数先增加后减小，荔枝面静摩擦系数逐渐减小，这是由试验装置的系统误差和石材界面形貌特征较离散造成的.

2.3 滞回特性

(a) MC-1 (b) MC-2

(c) MC-3 (d) MC-4

(e) P-1 (f) P-2 (g) P-3

(h) BH-1 (i) BH-2 (j) BH-3图8 不同界面试件的滞回曲线Fig.8 Hysteresis curves of specimens with different interfaces

2.3.1 滞回曲线 不同界面试件的滞回曲线,如图8所示.由图8可知：1) 各曲线形状均近似为长方形，与小尺寸花岗岩界面[9]基本一致，表明不同界面砌缝承载能力均较稳定，变形性能及耗能能力均较良好，各界面加载及卸载刚度在加载过程中未发生明显退化；2) 在第一循环中，机切面和抛光面试件的动摩擦力均有明显的非稳定阶段，机切面试件动摩擦力略有增大，抛光面动摩擦力先增大后减小；3) 各界面摩擦力均随竖向压应力的增加而增大，这是因为界面主要依靠摩擦耗能，故其耗能能力随竖向压力的增大而增加.

2.3.2 动摩擦系数 动摩擦系数是反应砌缝耗能能力和承载能力的主要参数.3种试件的各加载循环平均动摩擦系数,如图9所示.图9中：N为加载次数；μ为平均动摩擦系数.

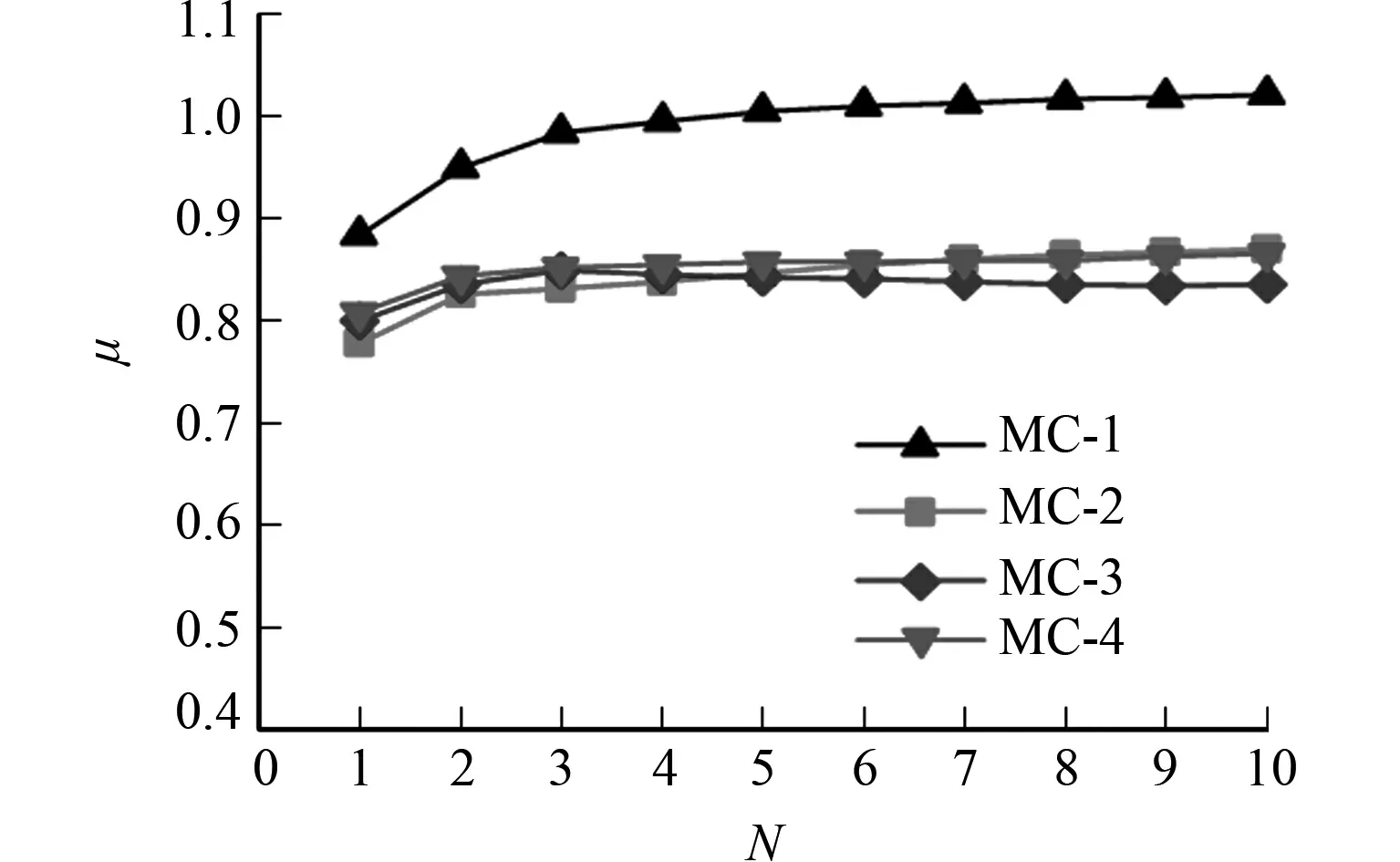
(a) 机切面

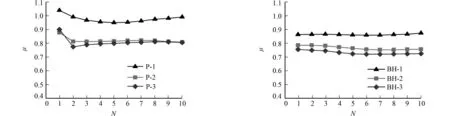
(b) 抛光面 (c) 荔枝面图9 3种试件的各加载循环平均动摩擦系数Fig.9 Average sliding friction coefficient of three types of specimens in each loading cycle

1) 机切面和抛光面试件的动摩擦系数在经历一次加载循环后才趋于稳定;荔枝面试件的动摩擦系数在起滑后基本处于稳定状态.这是由于荔枝面微凸体尺寸较小，局部接触面强度较低，在滑动初期迅速被磨蚀，使界面较快进入整体接触稳定摩擦状态.2) 当竖向压应力为0.2 MPa时,试件动摩擦系数较大；当竖向压应力为0.4，0.6 MPa时，试件的动摩擦系数较接近.这是由低应力下加载装置相对较大的系统误差所造成的.3) 当竖向压应力为0.4，0.6 MPa时，机切面与荔枝面试件的动摩擦系数较接近，且略大于荔枝面；机切面、抛光面和荔枝面试件平均动摩擦系数分别为0.84,0.82和0.75.这主要是由于类“犁沟效应”产生的犁削力增大了抛光界面及机切界面间的抵抗力，同时，荔枝界面加载过程中产生的大量石粉起到了润滑的作用.4) 机切面及抛光面的动摩擦系数大于小尺寸界面[8-9]，荔枝面的动摩擦系数近似等于小尺寸界面[8].这是由于石材尺寸较大，加工技术难以保证机切界面及抛光界面完全平整，进而导致压剪作用下界面发生类“犁沟效应”，使试件的动摩擦系数偏大.

3 抗剪强度计算

砌体灰缝的受剪破坏通常符合摩尔库伦准则，其表达式为

τ=σ·tanφ+c.

上式中:σ，τ分别表示界面竖向压应力及水平剪应力；c为粘结力，对于干砌灰缝，通常假定其等于0[7]；φ为内摩擦角.

图10 拟合公式的计算值与试验值的对比Fig.10 Comparison between calculation values of fitting formula and test values

内摩擦角可通过试件水平剪应力与竖向压应力关系曲线拟合求得，曲线斜率即为内摩擦角.由于在竖向压应力为0.2 MPa下，测得的试验结果误差较大，因此，仅采用竖向压应力为0.4，0.6 MPa下的试验结果进行拟合，得到机切面、抛光面和荔枝面试件的内摩擦角分别为39°,40°和37°.荔枝面内摩擦角近似等于小尺寸界面[8].由于类“犁沟效应”，机切面和抛光面的内摩擦角均大于小尺寸界面[8-9].

拟合公式的计算值与试验值的对比，如图10所示.由图10可知：拟合公式的计算值与试验值吻合良好.

4 结论

1) 条石无浆砌缝在压剪复合作用下经历了弹性、界面磨损和摩擦滑移3个阶段.

2) 条石砌缝的滞回曲线饱满，形状呈矩形；其摩擦滑移阶段表现出优越的耗能能力，试件滞回耗能随竖向压力水平的提高而增加.

3) 受限于石材表面加工技术精度，砌缝界面磨蚀特征揭示机器切割界面和抛光界面表现为局部不平整接触，导致往复荷载作用下，砌缝界面发生类“犁沟效应”.

4) 机器切割和抛光界面的动摩擦力因类“犁沟效应”有所增大，使这两种界面摩擦系数较接近，且均大于荔枝界面.机切面、抛光面和荔枝面平均动摩擦系数分别为0.84,0.82,0.75.

5) 基于摩尔-库伦准则和试验数据分析，提出砌缝抗剪强度计算公式，计算值与试验值吻合良好.