部分充填式钢箱-混凝土连续组合梁刚度分析

莫时旭， 蒋越， 郑艳， 韩涛

(1. 桂林理工大学 土木与建筑工程学院， 广西 桂林 541004；2. 桂林理工大学 广西建筑新能源与节能重点实验室， 广西 桂林 541004)

交通与桥梁的发展是我国经济与科技发展的基础，是我国综合实力的体现因素之一[1].近几十年来，随着我国经济的高速增长，钢铁工业飞速发展，钢年产量近十亿吨，为钢结构和钢混组合结构桥梁的发展打下了坚实的物质基础.2015年5月，交通部发布了《对我国桥梁技术发展战略的思考》的研究报告；2016年8月，交通部发布了《关于推进公路钢结构桥梁建设的指导意见》，这类政策和报告的发布为钢结构与组合结构的发展创造了新的发展机遇，有利于促进我国公路桥梁向资源节约、环境友好型发展[2-3].钢箱混凝土组合梁因性能优良，在我国桥梁工程中得到广泛应用，国内外学者也对其开展了大量的研究[4-11].美国结构设计规范在考虑界面滑移影响的基础上，推导出和剪力连接程度有关的计算梁有效刚度的简化公式[12].童根树等[13]提出组合系数法，避免了钢箱梁和混凝土板绕自身形心轴的抗弯刚度进行折减的问题.胡夏闽等[14]考虑了钢箱混凝土组合梁界面的相对滑移，提出钢混凝土组合梁挠度计算的附加曲率法.GBJ 17-88《钢结构设计规范》[15]运用换算截面法计算组合梁截面的抗弯刚度，该方法步骤简单，但没有考虑两种材料的滑移效应.现行规范GB 50017-2017《钢结构设计规范》[16]采用聂建国提出的折减刚度法.由于混凝土和钢梁的交接面的滑移导致附加曲率的产生，从而使截面的弹性抗弯承载力减小，聂建国则推导了滑移移效应引起的附加挠度计算公式.本文设计了3组不同抗剪连接度的试验梁，将理论与试验数据结合，对部分充填式窄幅钢箱-混凝土连续组合梁进行刚度分析.

1 试验概况

1.1 试件设计

设计3根充填式窄幅钢箱-混凝土连续组合梁试件，编号分别为PFSCB1，PFSCB2，PFSCB3.试验梁的长度为6.40 m,高度为0.42 m.钢箱采用Q235钢板，顶板与底板厚度均为10 mm，腹板厚度为4 mm.试验梁立面和负弯矩区横截面图,如图1所示.

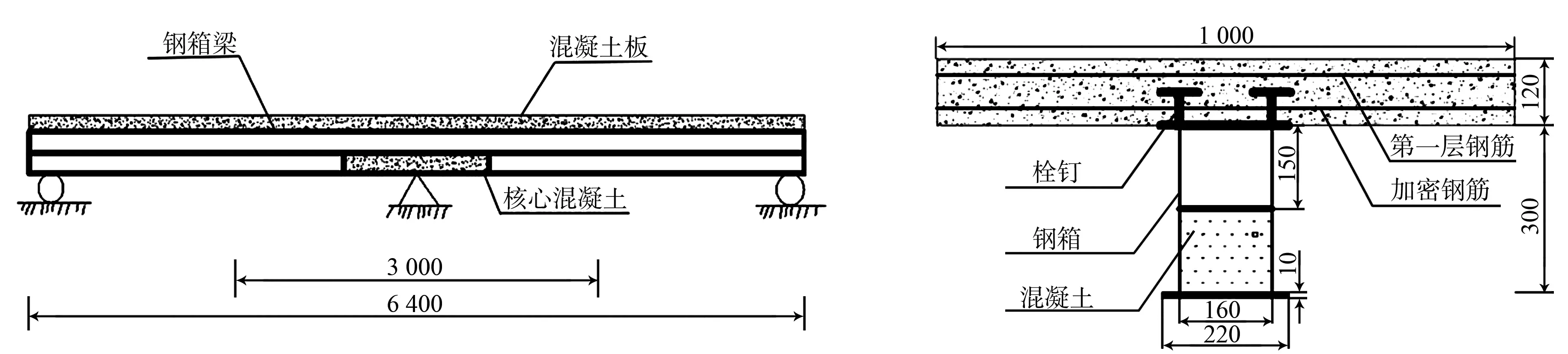
(a) 立面 (b) 负弯矩区横截面图1 试验梁立面和负弯矩区横截面图(单位：mm)Fig.1 Elevation and section diagram of negative moment zone of test beam (unit: mm)

采用直径为13 mm的4.8级普通栓连接混凝土面板与钢箱，抗剪连接度通过栓钉间距设定.栓钉分区示意图，如图2所示.栓钉布置参数，如表1所示.表1中：n为栓钉数量；s为栓钉间距.

图2 栓钉分区示意图Fig.2 Schematic diagram of stud division

表1 栓钉布置参数
Tab.1 Arrangement parameters of studs

试件编号抗剪连接度M1区(左右两侧)n/个s/mmM2区(中间区域)n/个s/mmPFSCB11.00221503490PFSCB20.751621526120PFSCB30.501230018176

1.2 材料力学性能

按照标准金属材料拉伸试验方法，测试钢材中钢板和钢筋的力学性能.栓钉的抗剪承载力采用ECCS标准推出试验，通过计算得到单根栓钉抗剪承载力为72 kN.

钢材的力学性能，如表2所示.表2中：φ，d分别为钢筋直径和钢板厚度；fy为屈服强度；ft为抗拉强度；E为弹性模量.

28 d时和试验时,实测的混凝土力学性能，如表3所示.表3中：fcu,W，fcu,B分别表示混凝土翼板立方体抗压强度和混凝土箱内立方体抗压强度.

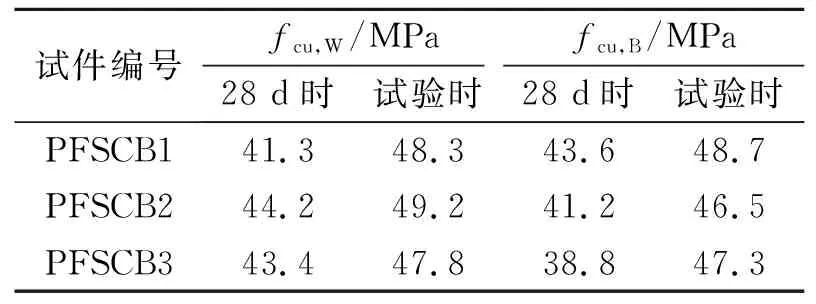
表3 混凝土力学性能Tab.3 Mechanical properties of concrete

表2 钢材的力学性能Tab.2 Mechanical properties of steel

图3 加载装置Fig.3 Loading device

1.3 试验装置及加载方案

采用静力加载的方式，加载装置，如图3所示.将千斤顶放置在两跨连续实验梁跨中的位置，在试件梁的跨中、中支座截面处相应的位置布置电阻应变片，两端支座及加载点处放置压力传感器.

试验梁硂面板及钢箱应变片布置，如图4所示.在组合梁的支座，L/4，L/2，3L/4(L为试验梁的总长度)截面混凝土翼板与钢箱界面处安置数显式千分表，用于测量翼板、支座的位移和钢箱相对滑移.在试验过程中，使用裂缝放大器测量裂缝宽度，并观察裂缝发展情况.

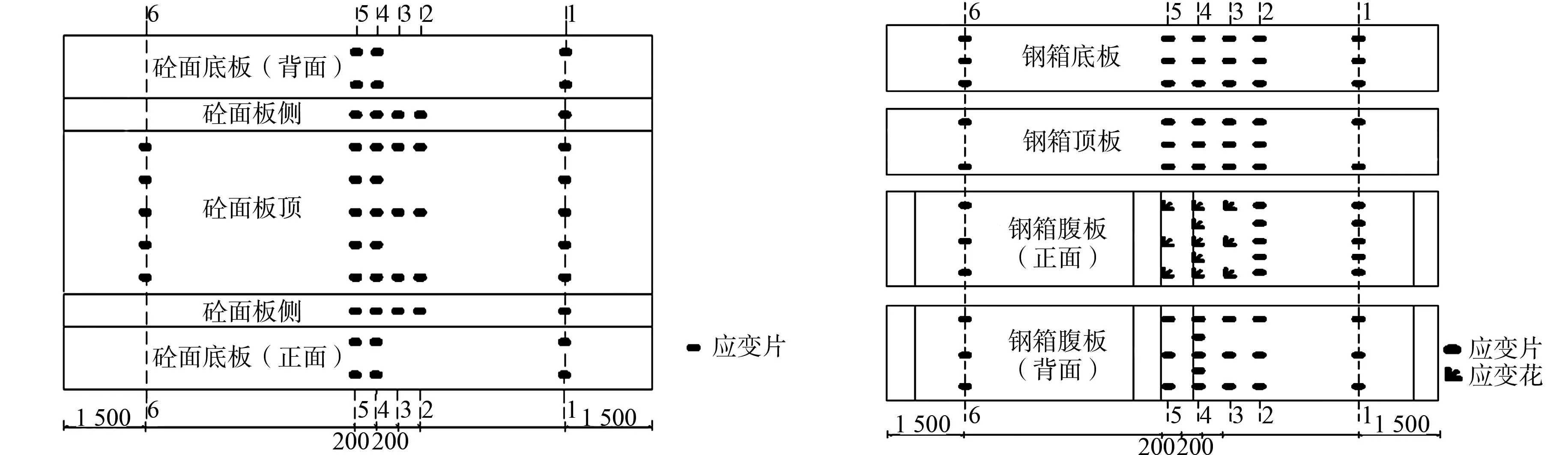
(a) 砼面板应变片 (b) 钢箱应变片图4 硂面板与钢箱应变片布置图(单位：mm)Fig.4 Layout of concrete panel and steel box strain gauge (unit: mm)

2 试验现象及破坏模式

2.1 试验现象

各梁的实验现象大致相同，现以试验梁PFSCB3为例，介绍梁的实验过程及现象.当加载到120 kN左右时，混凝土翼板中支座处出现了第一条可见裂缝，随着荷载增加，裂缝宽度增加，同时生成其他裂缝;当加载到240 kN左右时，中支座处的混凝土翼板出现第一条贯通裂缝;当加载到360 kN左右时，听到“砰”的声响，表明钢箱与混凝土翼板交界面处自然粘结破坏;当加载到400～600 kN时，出现“咔”的声响，混凝土下翼缘出现较大裂缝；当加载超过600 kN时，梁的钢箱腹板发生屈曲；当加载达到800 kN时，到达极限承载阶段，此时，混凝土翼板出现大量贯通裂缝.

2.2 破坏模式

每根梁的破坏模式各有差异.试验梁PFSCB1的破坏形态，如图5(a)所示.由图5(a)可知：因为梁跨中截面区钢箱底板的焊接裂缝拉裂而造成突然破坏，此时，梁的钢箱腹板未完全屈曲且梁的混凝土翼板未完全压碎；剥开钢箱，核心混凝土下部有多条裂缝，但都未完全贯通.试验梁PFSCB2的破坏形态，如图5(b)所示.由图5(b)可知：跨中截面混凝土翼板底面出现较多贯通裂缝，说明在梁跨中截面的中心轴已经向上移至混凝土翼板;试验梁钢箱跨中正弯矩区至反弯点附近产生近似斜向45°外鼓屈曲波，由于正弯矩区段为空钢箱梁，屈曲波发展范围较大，但受到钢箱顶底板约束作用较强，顶底板没有出现屈曲;剥开钢箱，发现核心混凝土沿剪切面断裂，是典型的剪切破坏.试验梁PFSCB3的破坏形态,如图5(c),(d)所示.由图5(c),(d)可知：混凝土翼板顶面的裂缝开展较少，梁的跨中截面钢箱腹板出现一条45°斜向屈曲内凹，从负弯矩区填充混凝土段上箱室延伸至正弯矩区未填充混凝土下箱室；负弯矩区段填充混凝土后抑制了腹板的内屈，下箱室腹板屈曲不明显；剥开钢箱，发现核心混凝土棱柱体依旧保持着整体性，说明钢箱的约束充分发挥了作用;内部填充的核心混凝土产生剪切斜裂缝，组合梁承载能力没有明显下降，表现出良好的延性.

(a) PFSCB1 (b) PFSCB2

(c) PFSCB3表面图 (d) PFSCB3内部图图5 试验梁的破坏形态Fig.5 Failure mode of test beam

3 实验结果与分析

3.1 荷载-挠度曲线

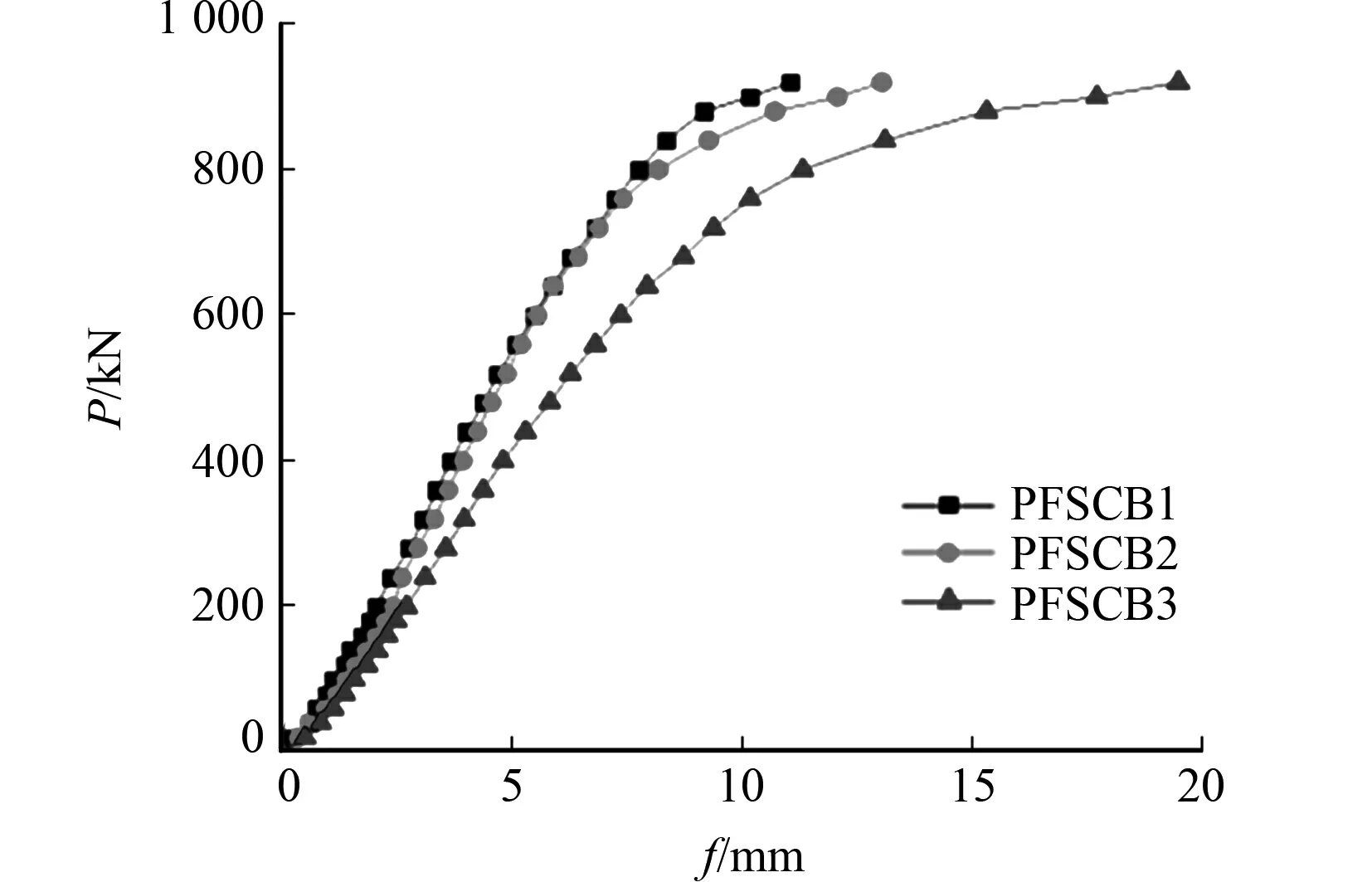
图6 试验梁的跨中荷载-挠度曲线Fig.6 Load-deflection curve of test beam

挠度值可直接反映组合梁在各阶段的受力性能.试验梁的跨中荷载(P)-挠度(f)曲线,如图6所示.由图6可知：在开始加载时，试验梁处于弹性工作阶段，充分发挥了组合梁的组合效应，3组试验梁的挠度随荷载的变化趋势比较相近，曲线都呈线性变化，挠度缓慢增加，说明试验梁在弹性工作阶段的抗剪连接度对挠度值的影响较小；当加载至弹塑性工作阶段时，曲线的曲率开始逐渐增大，组合梁挠度随荷载增加变化明显，该阶段抗剪连接度较大的试验梁PFSCB1的挠度值增长最为缓慢；当继续加载至塑性阶段时，荷载-挠度曲线慢慢变平，此时，钢箱梁的变形速度明显快于荷载的增加速率；在所受荷载相同的情况下，抗剪连接度最大的试验梁PFSCB1的挠度值最小.

3.2 钢箱底板的荷载-应变曲线

钢箱底板中支座的荷载-应变(ε)曲线，如图7(a)所示.由图7(a)可知：在加载初期，3组试验梁钢箱梁底板的荷载-应变曲线较为接近，基本呈线性变化；当进入塑性阶段，试验梁充分发挥材料的强度；试验梁PFSCB1应变急剧增加，说明中支座负弯矩区底板受拉而出现局部屈曲，组合梁的整体刚度变小、变形增大；试验梁PFSCB2，PFSCB3应变增大也较为明显，但是应变曲线与PFSCB1相比较为缓和；在塑性破坏阶段，随着荷载增加，应变增加的速度变快，直至钢箱破坏，应变值不再随荷载增加.

钢箱底板跨中的荷载-应变曲线，如图7(b)所示.由图7(b)可知：在受力开始时，曲线呈线性变化，混凝土翼板与钢箱梁组合效应良好；随着荷载的增加，由于连续组合梁跨中位置为空钢箱，没有核心混凝土与钢箱梁一起承担荷载，所以组合梁跨中截面变形较大；当荷载加至0.8 Pa时，钢箱梁底板荷载应变曲线出现了小小的突变，局部屈曲速率加快，使应变急剧的增加；在塑性破坏阶段，荷载-应变曲线较为缓和是因为形成了塑性铰，使连续组合梁发生弯矩重分布.

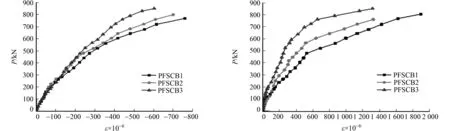
(a) 中支座 (b) 跨中图7 钢箱底板中支座和跨中的荷载-应变曲线Fig.7 Load-strain curve of steel box middle support and midspan of steel box bottom slab

3.3 截面高度-应变分布

沿梁高方向，在连续组合梁中支座截面和跨中截面粘贴1竖排5片间距为50 mm的应变片，用于测量钢箱腹板在荷载作用下的应变.试验梁PFSCB1中支座截面和跨中截面的应变分布,如图8所示.图8中：h为钢箱截面高度.由图8(a)可知：在荷载达到80%的极限荷载以前，试验梁处于弹性阶段，应变值沿梁高呈线性关系，满足平截面假定；随着荷载的增加，钢箱梁出现局部屈曲，导致试验梁的刚度不断减小，钢箱应变值增大明显;当试验梁处于弹塑性工作阶段时，钢箱梁跨中位置局部屈曲加剧，中支座附近塑性铰慢慢形成，使中性轴略有上升.由此可知,试验梁的组合效应增加了梁体的延性和刚度.

由图8(b)可知：试验梁跨中部位为正弯矩区，在翼板受压而钢梁受拉时，钢梁内无核心混凝土共同承担受力，因此，试验梁翼板在整个受力过程中承担较大的承载力.在弹性工作阶段，跨中部位腹板应变随梁高呈线性变化，基本符合平截面假定.在弹塑性工作阶段，钢梁腹板应变出现突变，试验梁跨中截面钢箱受到较大的压应力而发生局部屈曲，屈曲呈现正弦波状起伏的屈曲形态，而翼板还具有较好的抗压承载能力，中和轴开始慢慢上移.与中支座区相比，跨中区钢梁产生的局部屈曲行为更为明显，中性轴更靠近钢箱顶板.

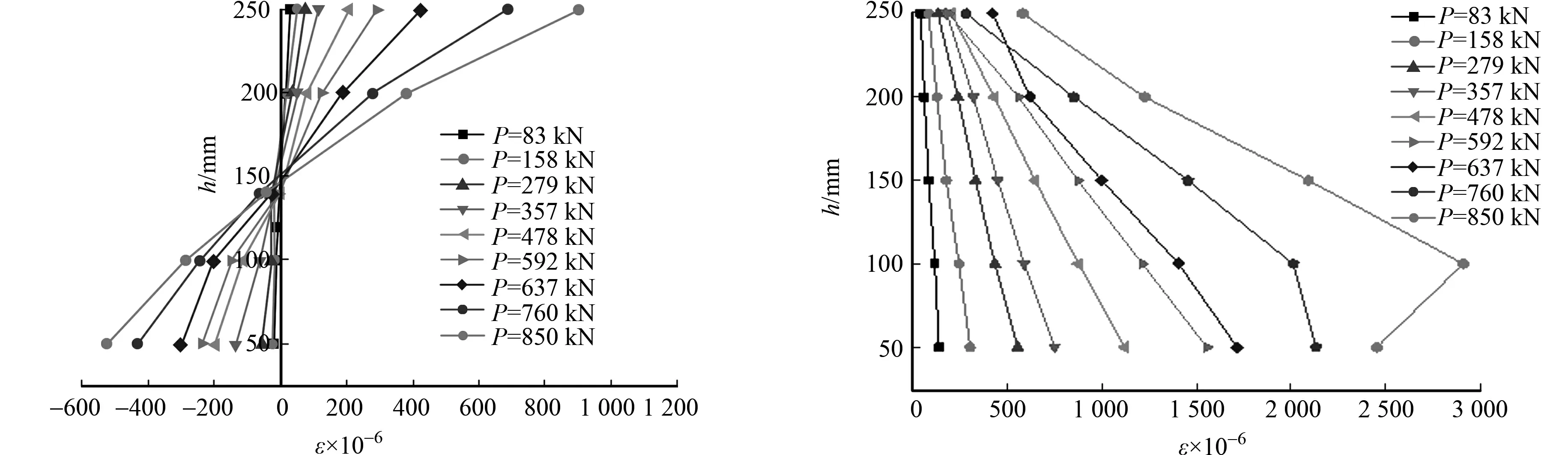
(a) 中支座截面 (b) 跨中截面图8 试验梁PFSCB1中支座截面和跨中截面的应变分布Fig.8 Strain distribution of middle support section and mid-span section of PFSCB1 test beam

4 刚度分析

连续组合梁中支座区钢箱下翼缘充填部分混凝土.假设钢箱和混凝土均为理想弹性体，符合平截面假定.采用换算截面法计算钢箱的截面特性，即把混凝土截面换算成等效的钢截面.

1) 中和轴位于核心混凝土处(x≪hc).

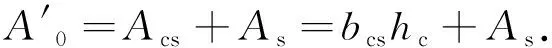
(1)

组合截面中和轴至钢箱底板的距离x为

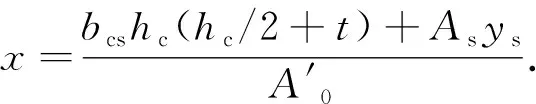
(2)

组合截面的惯性矩Is为

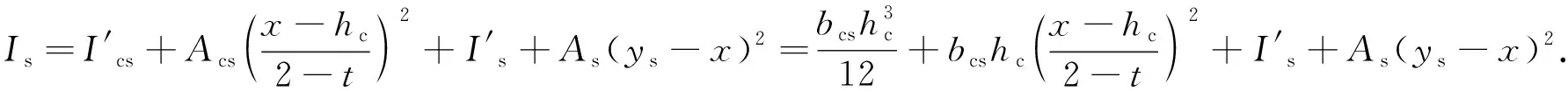
(3)

2) 中和轴位于非核心混凝土处(x>hc).

组合截面面积为

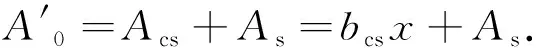
(4)

组合截面中和轴至钢箱底板的距离为

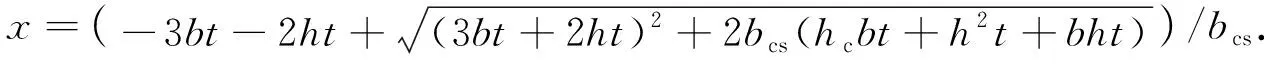
(5)

组合截面的惯性矩为

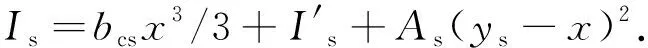
(6)

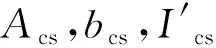
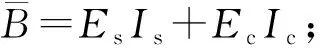
考虑边界条件对刚度的影响,王立宪等[17]提出折减刚度系数ζ,其表达式为

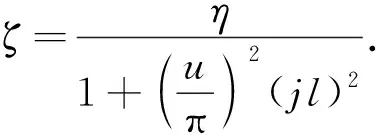
(7)

式(7)中：u为计算长度因子，此处取值为0.5；其他参数及推导见文献[17].

为了简化式子，引入常数v，w，则有

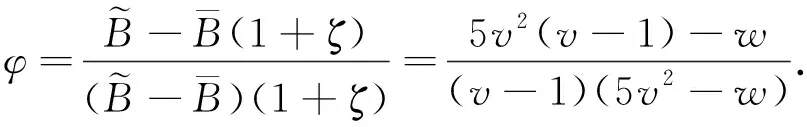
(8)

将钢箱-混凝土组合梁和空钢箱梁跨中的挠度计算值与实测值进行比较，如表4所示.表4中：f为钢箱-混凝土组合梁挠度的实测值；f′为钢箱-混凝土梁挠度的计算值；f″为空钢箱梁挠度的计算值.

表4 挠度计算值与实测值的对比Tab.4 Comparison of calculated and measured deflection values

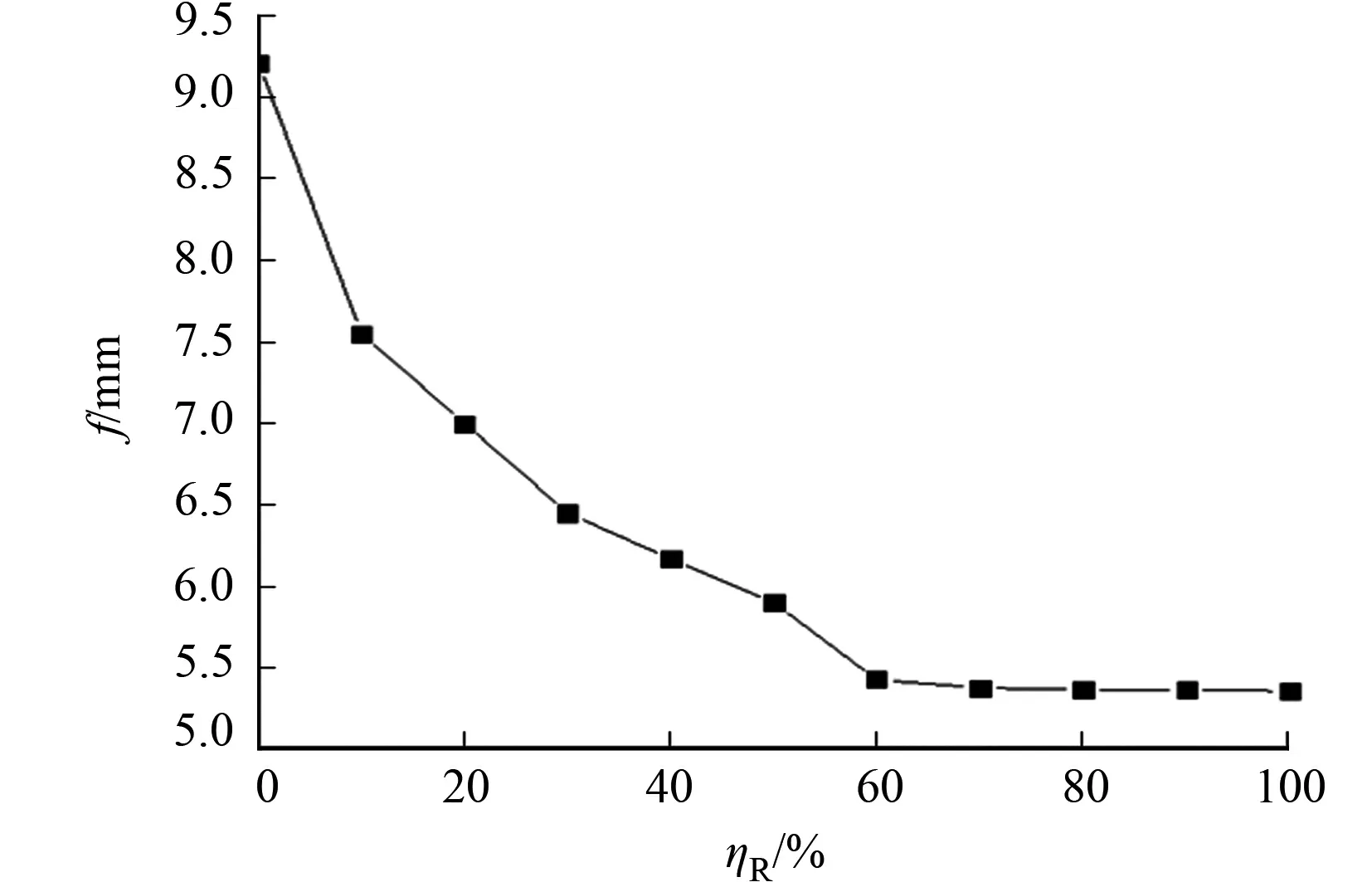
图9 箱内充填混凝土量与跨中挠度计算值的关系Fig.9 Relationship between amount of concrete filled in box and calculation mid-span deflection

由表4可知：组合梁的抗剪连接度越大，其挠度值越小；钢箱-混凝土组合梁的计算值大于实测值，且计算精度在合理范围内；在所受荷载相同的情况下，与空钢箱梁相比，钢箱-混凝土组合梁的挠度值减小20%左右，说明钢箱内部分充填混凝土对挠度有很大的影响，钢箱-混凝土组合梁比空钢箱梁有更高的承载能力和更好的延性.

在组合梁抗剪连接度为1.00的情况下，计算由空钢箱(混凝土充填量ηR=0%)到全充填(ηR=100%)时组合梁的挠度.箱内充填混凝土量与跨中挠度计算值的关系，如图9所示.由图9可知：从空钢箱至ηR为10%时,挠度下降最快;当ηR为10%～60%时，挠度下降稍微缓慢；当ηR为60%时，发生突变直至全填充，挠度基本保持不变.由此可知，随着组合梁箱内混凝土充填量的增加，箱内受压区逐渐提高，当ηR达到60%后，箱内受压区保持不变，使部分充填混凝土受拉.

5 结论

对3根部分充填式窄幅钢箱混凝土连续组合梁进行反向加载试验，分析组合梁的变形情况，并对刚度计算方法进行研究，得到以下3点结论.

1) 钢箱混凝土组合梁的挠度与抗剪连接度有关.在弹性阶段，组合梁的抗剪连接度越大，挠度越小，当抗剪连接度达到0.75后，挠度变化较小.

2) 在组合梁钢箱内充填混凝土限制了钢梁在受力时发生内屈，不仅提高了钢箱混凝土连续组合的承载能力，还增加了梁体的刚度和延性.计算结果表明，组合梁钢箱内充填混凝土比空钢箱的挠度值减小了20%左右.

3) 当组合梁抗剪连接度为1.00，钢箱内混凝土充填量从0%增加至60%时，挠度值随着充填量的增大而减小；当充填量达到60%以后，挠度值基本不变.因此，钢箱内混凝土充填量为60%时，组合梁的刚度提高最明显.