考虑能耗的混流装配线物料配送多目标调度方法
周炳海, 费芊然
(同济大学 机械与能源工程学院, 上海 201804)
目前关于混流装配线物料配送问题的研究,多以最小化碳排放或耗电量为目标,考虑能耗的研究较少.如Xiao等[1]提出模拟退火算法,解决以最小化碳排放为目标的车辆路径问题(vehicle routing problem,VRP);Ilgin等[2]则以最小化车辆总行驶距离和耗电量为目标解决VRP问题.
混流装配线边的零件进料问题为NP-hard问题[3],因此精确算法只适合求解小规模的零件配送问题;而求解大规模的零件配送问题常用元启发式算法,如Fathi等[4]提出一种改进粒子群优化算法解决以多载量小车运输行程和运载量为优化目标的装配线零件进料问题,Nouri 等[5]则考虑多个机器人的车间机器人路径规划问题,并提出基于邻域的遗传算法来优化作业完成时间.
在分析上述文献基础上,本文提出了考虑能耗的零件配送问题,引入“转运”策略以减少能耗,即允许送料机器人对配送物料进行拆分、交换等操作,并构建变邻域搜索策略的改进型离散差分进化算法对送料机器人进行调度,以期最小化配送系统的送料机器人团队规模及总能耗.
1 数学建模
1.1 问题描述
在线边超市配送系统[6]中,装配所需的物料统一存放在装配工位旁的线边超市中,送料机器人根据生产计划对各目标工位的JIS(just-in-sequence)料箱进行配送.机器人在配送过程中能量耗尽时需进行充能,且在此期间无法执行配送任务,因此需要重新分配补料任务,极大地增加了调度的复杂度.
送料机器人的能耗主要与其载重及行驶距离有关[7],为了减少配送过程中的机器人能耗,本文提出图1所示的 “转运”策略,即在配送过程中,允许送料机器人将其配送任务内的物料暂存在线边超市或工位处,交由其他送料机器人进行配送.该策略可以有效地缩短送料机器人配送任务中的行驶距离并优化载重分配,从而减少能耗.许多学者已经建立了若干能耗模型,用以确定单位行驶距离的能耗与机器人载重量之间的关系.基于Qiu等[8]的研究,本文采用式(1)计算机器人r在工位s和s′之间行驶的能耗:
(1)

为了解决考虑能耗的机器人物料配送调度问题,做出如下具体假设:① 机器人装卸料的能耗忽略不计;②机器人往来物料超市的工位间的速度为定值;③机器人的充电时间为定值,机器人返回后最早可于下一节拍开始工作;④同一机器人完成的不同补货任务的补货时间不能重叠;⑤不同机器人在同个工位进行的不同补货任务的时间不能重叠;⑥物料自物料超市出发可经由多个机器人配送到目标工位;⑦物料的转运操作只能在物料超市和各工位处发生;⑧机器人在一个节拍中最多补料一趟;⑨机器人的载重量和工位库存容量均用标准化箱的数量表示.
1.2 数学模型
1) 参数及其定义:
S装配线的工位集合,且工位s=1,2,…,|S|;
R送料机器人集合,且机器人r=1,2,…,|R|;
T调度期间的生产节拍总数;
dst工位s在节拍t的物料需求量;
Bs工位s处JIS物料箱的容量;
Cr送料机器人r的物料配送能力;
v送料机器人的配送速度;
lss′工位s与s′之间的距离,且s,s′∈S∪{0},其中{0}表示线边超市;
tr送料机器人r卸载单位物料的时间;
m送料机器人未载重时的质量;
2) 决策变量:
kn送料机器人在工位n时对应的配送物料量;
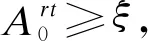
ξ机器人最低电量阈值.
3) 数学模型:
minf={f1,f2};
(2)
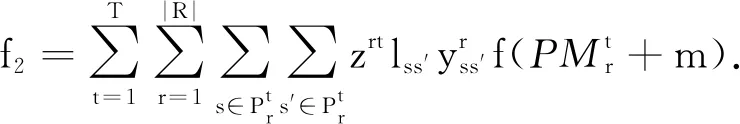
s.t.
∀s∈S;t=1,2,…,T.
(3)
∀r∈R;t=1,2,…,T.
(4)
∀r∈R;t=1,2,…,T.
(5)
(6)
(7)
∀s∈S;1≤t (8) ∀r∈R;t,t′=1,…,T;t≠t′; (9) (10) ∀r∈R;t=1,2,…,T; (11) (12) (13) zrt∈{0,1};∀r∈R;t=1,…,T. (14) 式(2)为目标函数,包含两个目标,分别为最小化机器人团队规模和最小化机器人总能耗.约束(3)和(4)分别表示工位容量限制和机器人配送能力限制;约束(5)和(6)保证每个机器人均从线边超市出发并返回;约束(7)确保任意机器人在某一时间仅在一个工位补料;约束(8)可避免不同机器人在同一时刻对同一工位进行补料的情况;约束(9)保证了机器人连续两次补料任务的时间差;约束(10)表示机器人到达工位时的电量;约束(11)确保机器人每次配送时的电量不低于安全电量;约束(12)~(14)为二进制变量. 由于混流装配线边的零件配送问题为NP-hard问题[3],采用启发式算法可以更有效地在可接受时间内解决问题.多目标差分进化算法是基于群体智能理论的优化算法,具有较强的鲁棒性和全局寻优能力.本文构建变邻域搜索策略的改进型离散差分进化算法VNS-MDDE(multi-objective discrete differential evolution algorithm with variable neighborhood search),在多目标差分进化算法的基础上引入变邻域搜索策略进行局部优化. VNS-MDDE算法采用混合双层编码方式,如图2所示,编码的长度为优化问题中装配线工位的总数|S|的两倍,其中后|S|个工位为转运工位.第一层编码表示机器人服务工位的详细信息,第二层表示机器人的配送物料量. 选择合适的初始种群能加快算法的收敛并影响解的优劣.根据上述编码形式,本文采用最近邻启发式(NNH)算法构建初始可行解,步骤如下: ① 令t=1. ② 选取机器人r=1,从超市出发随机服务某个工位s.如果服务该工位可行时,即满足约束(3)~(14),则前往工位s=s+1,否则该机器人返回超市,下一个机器人从超市出发(r=r+1).直到所有工位s的物料需求均被满足为止. ③t←t+1. ④ 重复步骤②和③,直至t=T为止. 重复上述步骤②~⑤共N次,生成初始种群. 本文算法采用的是差分进化算法(differential evolution algorithm,简称DE)中标准的变异策略DE/rand/1[9].根据一般的DE变异算子的结构,在第G次迭代时,在种群中随机选择3个个体,通过把2个个体之间的加权向量差加到第3个个体上来产生新的变异个体Vi(G).本文采用如下针对整数规划和混合整数规划的变异算子来生成变异个体: Vi(G)=Xa(G-1)⊕F⊗(Xb(G-1)-Xc(G-1)). (15) 式中:a,b,c∈{1,…,N}是随机选择的,且a≠b≠c≠i;F∈[0,1]是控制偏差变量放大的变异常数因子.等式(15)的等号右侧由两部分运算组成.第一部分表示两个个体Xb和Xc之间的加权差,用下列等式表示: Δi(G)=F⊗(Xb(G-1)-Xc(G-1))⟺ (16) 其中Δi(G)=δi1(G),…,δi,T-1(G)是临时变量,rand(j)是[0,1]之间的随机数.第二部分表示Δi(G)和目标个体的加和,用下列等式表示: Vi(G)=Xa(G-1)⊕Δi(G)⟺ vij(G)=xaj(G-1)⊕δij(G)= (18) 式中 %表示模运算符,用来计算其左边的整数除以其右边的整数得到的余数. 交叉算子是指将变异个体的参数与另外预定的目标个体按一定规则混合来产生试验个体.其中通过将变异个体和父代个体Xi(G-1)组合得到交叉个体Ui(G),交叉个体的形成过程如下: 在交叉运算之后,选择算子将决定试验个体是否可以保存至下一次迭代.本文将使用非支配排序方法将种群分成各个非支配层,随后计算各层级每个个体的拥挤度[10],最后在Ui(G)和Xi(G-1)中选择优者成为Xi(G). 为了增强其局部搜索的能力,本文在每次迭代过程中加入变邻域搜索策略(VNS),对结构邻域内的解进行搜寻改进.VNS的思路是在不同的邻域结构N1,…,Nk之间进行搜索.从第一个邻域结构开始进行局部搜索,直到无法进一步地改进为止.本文提出的邻域结构如下: 随机交换(random exchange,RE):随机选择Z对机器人,交换其服务工位的配送物料量. 随机转移(random remove,RR):随机删除机器人r在周期t的配送任务,将其配送物料随机分配给其他机器人配送. 贪婪转移(greedy shift,GE):该邻域结构依据贪婪算法的思想,将周期t内配送距离最长的机器人的配送任务删除,并逐个分配到使机器人配送距离增加最少的配送计划中. 转运(optional transfer,OT):根据性质3选择Z对机器人执行转运操作. VNS-MDDE算法流程如图3所示.当装配线工位数、机器人数量和生产节拍分别为|S|,|R|和T时,算法的时间复杂度为O(|S|·|R|·T);随着工位数、生产节拍数及待分配机器人数量的增加,计算复杂度将会大幅上升.VNS-MDDE基本操作及最坏情况下的复杂度如下: ① 在一次迭代中从候选解中找出非支配解O(2N); ② 用非支配排序和拥挤度计算方法,从数量为2N的候选解中选取N个解:O(4N2)+O(2N×lb(2N)); ③ 选取解在邻域结构中进行优化,即O(N×Z). 因此,VNS-MDDE算法的复杂度约为O(4N2),可见该算法的计算复杂度合理,可以有效地得出最优解. 为了测试本文提出的VNS-MDDE算法的性能,在Intel Core i5-7300U,2.71GHz CPU,8GB RAM内存的计算机上使用MATLAB(2016a)对该算法进行了实验. 为了验证算法的有效性,基于文献[11]中汽车混流装配线零件进料问题及线边超市的相关实验参数构建实验算例.零件需求和工位初始库存均依据均匀分布随机生成,分别为[rnduni(0,4) ]和[rnduni(2,4) ],其中[·]表示四舍五入取整.每个机器人的最大载重Fmax为10箱,装配线的周期时间t和机器人在相邻工位及超市间的行走时间tw分别为90 s和5 s. NSGA-II和IBEA的结构和本文算法的结构相似,并具有权威性且应用广泛,因此将本文提出的VNS-MDDE算法与这两个标杆算法进行比较;此外,本文还将与最新的MOEA/CT算法[12]进行比较,该算法在MOEA算法的基础上提出了坐标转换策略、外部档案更新策略及多样性维护策略,以提高帕雷托前沿解集的多样性和收敛性.算法参数的设置如表1所示. 表1 多目标算法参数Table 1 Parameters of multi-objective algorithms 本文是多目标算法,用单一性能指标很难较好地评价多目标算法的性能,因此本文使用下列性能指标测试算法: ①非支配解的数量:λA=|NA|,其中NA表示算法A中找到的非支配解数量,非支配解的数量越多表示决策者选择范围越大. ③分布度指标: 为了验证VNS-MDDE算法的性能,将其与标杆算法NSGA-II,IBEA和MOEA/CT算法的测试结果进行对比.算例分为大、中、小三个规模,针对每个算例,各个算法均独立运行15次.分别计算三个规模下每个算法测试的三个性能指标λA,φA,Δ的平均值,如表2所示. 表2 算法的实验结果Table 2 Experiment results of algorithms 根据表2的实验结果,可以得出如下结论: ①根据表中λA指标值可知,VNS-MDDE算法找出的非支配解数量远多于NSGA-II和IBEA,并且随着问题规模的增加,它们之间的差距逐渐增大. ②根据表中φA指标值可知, VNS-MDDE找出的解的质量远优于NSGA-II和IBEA.比如在小规模问题中,NSGA-II和IBEA找出的非支配解集中大约有93%的解受到由VNS-MDDE得到的非支配解集中的解支配,而仅有5%的解支配VNS-MDDE算法找到的非支配解集中的解.这可以说明VNS-MDDE算法具有更优的搜索能力. ③根据表中Δ指标值可以看出,VNS-MDDE算法找出的非支配解的分布度值比其他算法更小,表明VNS-MDDE能进行更好的全局搜索. ④ VNS-MDDE算法和MOEA/CT算法在性能上相差不大,MOEA/CT算法在数量和分布度方面略优于本文算法;但是由于VNS-MDDE算法考虑了转运策略,而其他算法并无体现,因此其在寻优能力上表现最好. 除了算法运行结果对比,各算法运行时间对比如图4所示,当问题规模较小时(如组别1~6),4种算法的运行时间都很短,均低于500 s,其中,VNS-MDDE,NSGA-II和IBEA的运行时间基本相等.随着问题规模的扩大,各算法运行时间均有较大的增幅,尤其是MOEA/CT算法;但总体而言,各算法均在可接受的时间内解决机器人物料配送问题,并获得较优解. 以上对比测试证明了VNS-MDDE算法的有效性,表明该算法在处理大规模混流汽车装配线物料配送问题时能够提供满意解. 为分析各邻域结构对算法的影响,对|S|=20,T=30规模的算例进行重复实验,统计非支配解数量,结果如图5所示.图5直观地展现了各邻域结构对算法结果的影响,可以看出,OT的非支配解值的分布集中,RR次之,RE分布较散;邻域结构GE和OT均对非支配解具有优化作用,由此可知,转运可有效改善机器人物料配送的能源利用率. 本文对混流装配线线边集成超市的物料配送问题进行了研究,并提出了转运策略以降低能耗.针对该组合优化问题,采用最近邻启发式算法构建初始解,并在改进型离散差分进化算法的基础上引入变邻域策略进行局部搜索,构建了变邻域搜索策略的改进型离散差分进化算法(VNS-MDDE).最后,通过与NSGA-II,IBEA和MOEA/CT算法的对比验证了本文算法的可行性和优越性,该算法可有效地减少送料机器人的使用数量并降低能耗.后续可以对随机交换、随机转移、贪婪转移,以及转运等邻域结构进行更深入的研究,以提高VNS-MDDE在求解大规模问题时的效率和效果.1.3 问题性质




2 变邻域搜索策略的改进型离散差分进化算法(VNS-MDDE)
2.1 编码
2.2 种群初始化
2.3 变异运算
2.4 交叉运算
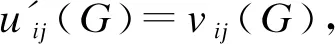
2.5 选择运算
2.6 局部优化
2.7 计算复杂度
3 实验与分析
3.1 实验参数

3.2 性能参数
3.3 算法对比实验及结果分析

3.4 邻域结构分析
4 结 语

