改进蚱蜢算法在电动汽车充换电站调度中的应用

王生生, 张 伟, 董如意, 李文辉

(1. 吉林大学 计算机科学与技术学院, 吉林 长春 130012; 2. 吉林大学 软件学院, 吉林 长春 130012; 3. 吉林化工学院 信息与控制工程学院，吉林省 吉林市 132022)

随着新能源汽车的发展,电动汽车在未来的电力负荷中将占有越来越大的比例,充换电站(battery swapping station, BSS)作为电动汽车主要的能源补给方式,其调度问题具有重要意义[1].群智能算法是通过模拟自然界生物种群的社会行为而提出的一种随机搜索方法;作为解决最优化问题的一种手段,目前已在与电动汽车充换电站调度相关的优化问题中得到了广泛应用.Jamian等[2]采用人工蜂群算法确定BSS的位置以减小负荷对配电网的影响.Yang等[3]对充电负荷问题建立负荷概率模型,并提出一种改进蚁群算法,对文中所提模型进行求解.Wu等[4]针对电池的充电损伤问题,以每块电池的充电方式为决策变量建立了最小化电池充电损坏模型,并采用PSO等多种优化算法对问题求解.Fang等[5]针对电动巴士运输调度问题,建立电动公交充电系统成本最小化模型,运用PSO-GA混合算法对问题进行求解.

根据所针对的问题,上述工作所建立的模型略有差异.为促进电网稳定运行,减小运行风险,本文采用的是比较常用的平抑负荷曲线模型[6],通过对比实验,发现此类问题的求解算法尚有一定的改进空间,很多现有工作没有尝试用最新的、改进的优化算法求解.本文通过实验测试了蚁狮优化算法(ant lion optimizer,ALO)[7]、飞蛾火焰优化算法(moth-flame optimization,MFO)[8]、鸟群算法(bird swarm algorithm,BSA)[9]等近期表现较优秀的群智能算法,以及IBAT[10]和IGPSO[11]等改进的群智能算法.结果发现,在解决此类问题时,上述较新的群智能算法虽然在不同程度上优于经典优化算法,但仍然存在陷入局部最优、收敛速度慢等问题.因此有必要寻找更高效的群智能算法以减小负荷波动并解决其他BSS优化调度问题.

受自然界中蚱蜢种群寻求食物过程的启发,2017年澳大利亚格里菲斯大学学者Mirjalil提出了蚱蜢优化算法(grasshopper optimization algorithm,GOA);对比实验分析表明,相比其他群智能算法,GOA具有一定的优势[12].

在实验过程中发现,虽然蚱蜢算法在解决充换电站调度问题上性能较上述算法[7-11]有所提高,但是收敛效果提升并不明显.由于BSS调度问题具有高维度、变量之间关系密切、对求解精度要求高等特点,故提出一种改进蚱蜢算法来解决充换电站调度问题.首先,针对粒子在随机搜索过程中超越边界限制的问题,提出一种基于对立点搜索的边界反弹机制;其次,为加强算法的全局搜索能力及防止种群陷入局部最优,采用正余弦算法搜索机制和Lévy飞行随机扰动机制;最后,使用非线性收敛策略的收敛因子提高算法的求解精度.同时还发现,本文所提出的改进蚱蜢算法对于其他文献所提出的BSS优化模型也具有更好的收敛效果.

1 蚱蜢优化算法GOA

1.1 算法背景

蚱蜢的生命周期主要分为三个阶段:虫卵、幼虫、成年个体.在幼虫和成年期具有一定的种群行为.在幼虫时期,大型的蚱蜢种群像滚动的皮球一样跳跃和移动,几乎吃掉行进道路上的所有植被;当蚱蜢进入成年期后,它们在空中形成一个种群进行远距离迁徙.运动缓慢、步伐小是蚱蜢幼虫期群体的主要特征,而长距离快速移动是成年期群体的基本特征.对于蚱蜢种群,另一个重要特征便是寻求食物来源——蚱蜢蜂拥而至.群智能算法在逻辑上将搜索过程分为两个部分:全局搜索和局部探优,模拟蚱蜢种群的社会行为实现了这两个功能及目标的搜寻过程.

1.2 优化过程

模拟蚱蜢种群行为的数学模型如下:

(1)

式中:Xi为第i个蚱蜢的位置;Si表示个体之间相互作用力;Gi是第i个蚱蜢的重力;Ai表示风向作用力;r1,r2和r3是[0,1]间的随机数;dij,dij分别表示第i个与第j个蚱蜢之间的距离及其空间向量;g是引力常数;u是漂移分量;ew,eg为单位矢量;s(d)是定义个体间力量强度的函数,d为个体间距离;f,l分别为吸引力强度和空间距离尺度.函数s(d)的主要作用是影响蚱蜢的社会行为，即个体间的吸引(s(d)<0,个体之间相互学习以寻找更优位置)和排斥(s(d)>0,个体之间相互排斥以防止陷入局部最优).

图1给出几组不同的l,f组合对函数s(d)的影响.

由图1可以看出,有些l和f的组合导致吸引区域特别小,如f=0,f=0.5,l=1.0等;而有些组合导致排斥区域过大或一直处于舒适区,如f=1时;为此算法通常选用f=0.5,l=1.5.

蚱蜢降落在地面上时,它们的位置阈值不低于0,但是在优化过程中种群的规模分布在自由空间中,使用式(1)会限制算法的全局搜索和局部探优能力,为此使用该方程的修改版本如下:

(2)

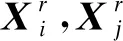
(3)

式中:cmax和cmin为收敛系数的最大值和最小值,文中分别取值为1,1×10-5;lit为当前迭代的次数;L为迭代总次数.

2 改进的蚱蜢优化算法IGOA

2.1 生成对立点的边界反弹机制

粒子在搜索过程中,容易跨过空间可行域,因此,GOA将超出可行域的粒子重新初始化在搜索区间边界位置;然而对于多数优化问题,其最优值一般不会在边界上取得,因此该方法对算法的寻优并没有起到实质性作用.相关研究证明了对立点搜索[13]在种群迭代过程中的有效性,故本文将超出边界的粒子重新初始化在搜索区间,并采用对立点搜索方法,通过竞争机制保留较优点.

(4)

2.2 基于正余弦的搜索机制

2016年,Mirjalili提出一种新的基于种群的优化算法(sine cosine algorithm,SCA)[14].SCA通过控制种群个体与最优个体之间的距离,以正弦和余弦函数的方程控制种群向最优解移动.算法的优点在于它能够使用比其他算法更少的运算符,使算法在搜索与探优之间达到平衡.SCA种群更新公式如下:

Xi(t+1)=

(5)

式中:a为常数2;参数β1为收敛因子,用以控制正弦和余弦的搜索范围;β2∈(0,2π)和β3∈(0,2)控制当前最优个体T距离种群个体Xi远近程度的影响;β4为[0,1]之间的随机数,用于选择正弦/余弦搜索方式;lit为当前迭代次数;L为总迭代次数.粒子通过正弦、余弦两种更新方式得到两个新个体,并通过竞争方式择优保留,增加了算法的寻优能力.

2.3 基于Lévy飞行的随机扰动机制

在正余弦机制下增加算法寻优能力的同时,为防止算法陷入局部最优,引入Lévy飞行机制对粒子随机扰动.动物在觅食的过程中,往往呈现出短距离搜索与长距离跨越的随机步伐,这种符合Lévy分布的随机搜索规则,目前在群智能领域已得到相关应用[15].Lévy飞行是非高斯分布的随机过程之一,简单数学公式可以写成:

(6)

式中:Lévystep为Lévy飞行的随机步长;Γ为标准伽马函数;β为常数且β=1.5.采用Lévy机制可使粒子在空间受到随机扰动,增加算法的寻优能力并且增加了种群跳出局部最优的概率.

2.4 非线性收敛系数

收敛系数c在算法的迭代过程中呈线性递减,但算法在迭代过程中并非呈线性收敛.为提高算法前期的搜索能力及后期的收敛能力,采用一种非线性收敛策略:

(7)

由式(7)可以看出,在算法迭代初期,函数斜率较小,c的减小速度较慢,使算法更好地搜索全局最优解;在算法后期,函数斜率逐渐变大,c的衰减程度提高,使得算法更加精确地寻找局部最优解,加快了算法的收敛速度.

综上,本文提出的IGOA更新公式如下:

(8)

(9)

式中:Lévywalk为飞行步长;Tr为当前最优个体;SCAupdate,GOAupdate分别对应正余弦、蚱蜢算法的两种更新方式,改进的蚱蜢算法见图2.

3 BSS优化调度的数学模型

3.1 充换电站运营方式

电动汽车充换电站是充电与换电一体化的服务场所,主要包括充电系统、电池更换系统等[16].当汽车电量不足产生换电需求时,车主将电动汽车驶入充换电站进行换电服务,工作人员将更换下来的电池进行充电,以完成电池的循环利用.

3.2 目标函数

大量的汽车电池充电行为将对电网造成巨大冲击,加剧电网负荷波动,威胁电网的安全稳定运行[17].为减小电网运行风险,防止“峰上加峰”,减小系统负荷波动,本文在前人工作的基础上,考虑电量需求等约束条件对模型进行优化,将1d均分为24个时段,N为1 d服务电动汽车的数量.以充换电站每个时间段的负荷功率为决策变量,以平抑负荷波动、减小负荷峰谷差为目标函数.

1)负荷离方差表示电网负荷波动的情况,值越小,代表负荷变化越平稳;故以电网负荷曲线均方差最小为目标函数:

(10)

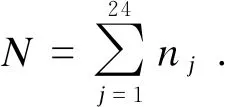
2)以负荷曲线峰谷差最小为目标函数:

(11)

式(10)和式(11)两个目标函数关系密切,互相影响,将其由多目标优化转为单目标优化.采用线性加权方法对函数作归一化处理:

minT=w1T1+w2T2.

(12)

式中w1,w2为两个目标函数的权重,且w1+w2=1.

3.3 约束条件

1) 电量需求约束:

(13)

式中:Qa为充换电站服务电动汽车一天的总电量;Pt为t时刻充换电站的负荷功率.为简化模型,本算例只考虑为电动汽车充电时所消耗的电量.

2) 功率约束:

Pmin≤Pt≤Pmax.

(14)

式中Pmin,Pt和Pmax分别为充换电站最小负荷功率、当前负荷功率和最大负荷功率.

3) 电池电量约束:

Qmin≤Qit≤Qmax.

(15)

式中:Qit为电池i在t时刻的电量;Qmin为最低电池电量,即产生换电需求的阈值;Qmax为电池的最高电量,即满电状态下的电量.

综上,电动汽车充换电站优化调度问题具有如下形式:

minT=w1T1+w2T2;

(16)

4 算例与实验分析

将本文提出的改进算法应用于目标函数,在计算机(CPU为3.0 GHz,16 GB内存,4 GB显存,Windows 10)上采用Matlab2014b进行仿真.

4.1 实验数据

本文受前人工作[18-19]的启发,在现实场景的基础上,通过模拟计算得出相应的实验数据.主要步骤如下:以中国北方某地区充换电站为例,基于该充换电站所在区域30天的历史负荷数据,通过模拟仿真计算得到该区域负荷曲线,作为实验算例的原始负荷曲线,如图3所示.假设该充换电站每天为100辆汽车提供服务,换电站中电池充电功率、负荷等主要数据综合参照了相关领域的文献[20-21].

4.2 实验结果

将本文提出的IGOA应用于目标函数,种群规模设为20,最大迭代次数为100次,并与ALO,MFO,BSA,IBAT,IGPSO,GOA[7-12],GA(遗传算法),PSO(粒子群算法),FPA(花朵授粉算法),GWO(灰狼优化算法)等算法[22-25]进行对比.考虑到迭代结果视图的可观性,挑选在该模型优化问题上表现相对良好的算法作为对比.结果如图4所示.

实验结果表明,在解决该模型问题上IGOA和GOA效率高于其他算法.ALO,MFO和IGPSO算法,在迭代前、中期易陷入局部最优,对本模型的求解精度相对较低;而BSA,IBAT算法,在迭代前、中期搜索能力差,导致求解精度较低;GOA和IGOA在本文模型求解过程中体现出一定的优势.而相对于GOA,IGOA的优越性主要体现在:①在算法初期,由于种群位置相对分散,搜索过程中容易超越边界范围,而以对立点为基础的边界反弹机制可以增加种群的多样性,增加了算法的寻优能力;②在算法中期,由于种群位置较为集中,活性降低,通过正余弦搜索与Lévy飞行扰动机制,增加了种群跳出局部最优的概率,曲线的下降速度要高于GOA算法;③在算法后期,控制因子采用非线性收敛策略,因此控制因子的斜率逐渐变大,增加了算法的局部搜索能力,使得曲线收敛效果更好.

以随机实验中的最优值2 485为参考,模拟出充换电站参与电网负荷的基础负荷曲线,并与经过IGOA优化后的负荷曲线对比,图5给出了24 h内优化前后的负荷曲线及原始负荷曲线.

可以看出,基础负荷曲线容易出现“峰上加峰”现象,在该情况下曲线的离差平方和、峰谷差较大;而从采用IGOA优化后的曲线可以明显看出,叠加后的曲线峰值小幅增大,曲线相对平稳,峰谷差以及离差平方和均明显减小,体现了IGOA解决该问题模型的有效性.

5 结 语

对电动汽车充换电站优化调度问题进行建模,并采用群智能算法对问题进行求解.针对现有群智能算法在解决该问题上的缺陷,提出了改进蚱蜢优化算法,并将其应用到充换电站优化调度问题上.通过对实验算例的测试,验证了算法的寻优能力、收敛速度等方面都好于现有群智能算法,并能较好地解决充换电站调度问题,提高了算法的性能.