珊瑚礁算法的改进研究

孔 芝, 李事成, 赵 杰

(东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004)

珊瑚礁优化(coral reef optimization,CRO)算法是Salcedo-Sanz等[1]在2013年，受到珊瑚虫繁衍生存过程的启发而提出的一种智能优化算法,用于处理多峰值函数优化问题.2014年，Pastor-Sanchez等[2]提出一种基于混合珊瑚礁-极限学习机的方法,并将其应用于风速预测系统中的特征选择,体现出优异的性能.2015年,Salce-Sanz等[3]提出一种具有和声搜索算子的珊瑚礁优化算法,并将其应用于风速预测中,得到良好结果.2016年, Pastor-Sanchez等[4]将珊瑚礁优化算法应用于多目标优化问题中,在计算资源有限的情况下表现出优异性能.同年, Salcedo-Sanz等[5]将珊瑚礁算法应用于微电网最佳电池优化调度问题,大大节省了总电费.2017年,Magdaleno等[6]利用珊瑚礁优化算法对调谐质量阻尼器进行结构振动控制,产生了极好的效果.同年,Jimenez-Fernandez等[7]提出一种物种珊瑚礁优化算法,并将其有效地应用于太阳能全球辐射重要参数缩减中.2018年,Duran-Rosal等[8]将珊瑚礁优化算法应用于缩减时间序列最佳尺寸中,显示出强大的分割能力.

目前为止,人们已经提出了许多改进的珊瑚礁优化算法[9-12],但这些算法在精度、收敛速度与避免陷入局部最优能力方面仍有待进一步提高.本文提出一种改进的珊瑚礁(improved coral reef optimization,ICRO)算法,通过对原珊瑚礁优化算法内部有性繁殖、无性繁殖和更替机制的改进,可以有效避免算法陷入局部最优,提高精度,并通过具体的测试函数证明了算法的优越性.

1 珊瑚礁算法

珊瑚礁优化算法是受到珊瑚虫繁衍生存过程的启发而提出的一种元启发式算法.珊瑚礁优化算法基本执行过程如下[13]:

①初始化:假设存在大小为M的珊瑚礁,即礁上存在M个节点空间供珊瑚虫生存;开始时,珊瑚礁上已有比例为ρ的空间被珊瑚虫占据,即礁上珊瑚虫的个数为M×ρ.

②外部有性繁殖和内部有性繁殖:珊瑚虫产生子代的方式分为两种,即外部有性繁殖和内部有性繁殖;其比例分别为ξ和1-ξ,即外部有性繁殖的珊瑚虫个数为M×ρ×ξ,内部有性繁殖的珊瑚虫个数为M×ρ×(1-ξ).外部有性繁殖的子代由雌雄异体的两个亲代产生,如式(1)所示;内部有性繁殖的子代由雌雄同体产生,如式(2)所示.

c1,α=[(1+φ)C1,α+(1-φ)C2,α]/2 ,c2,α=[(1-φ)C1,α+(1+φ)C2,α]/2 ，α=1,…,ψ.}

(1)

(2)

式中:C1和C2表示两个雌雄异体珊瑚虫,c1和c2表示其产生的两个子代;C表示雌雄同体珊瑚虫,c表示其产生的子代;α为迭代次数;φ为随机变量,其产生方式如下:

(3)

式中:κ为交叉常数;τ为0到1的随机数.

③更替机制:新产生的子代珊瑚虫需要占据珊瑚礁生存,此时珊瑚礁上有未被占据和已被占据的空间,其数量分别为M×(1-ρ)和M×ρ.若子代选择未被占据珊瑚礁,则可直接占据;若子代选择已被占据的珊瑚礁,则需与其上原有珊瑚虫进行适应度f(p)比较:若子代适应度高则占据该处,否则失败,继续尝试其他空间;若在最大占据次数μ内未完成占据,则子代珊瑚虫死亡.

④无性繁殖:当所有子代珊瑚虫完成珊瑚礁占据后,对现有珊瑚礁上的珊瑚虫进行适应度排序,选出比例为γ的高适应度珊瑚虫,让其通过无性繁殖(复制)的方式产生子代,并进行珊瑚礁的占据.

⑤毁灭机制:再一次进行适应度排序,选出比例为δ的低适应度珊瑚虫,将其毁灭.

进入循环,重复步骤②～⑤,直至满足终止条件,即达到最大迭代次数ψ.得出最优解.

2 改进的珊瑚礁算法

为了克服珊瑚礁优化算法的不足,本文对珊瑚礁优化算法进行了改进,主要涉及三个方面:内部有性繁殖方式、无性繁殖方式和更替方式.

2.1 内部有性繁殖方式改进

原始珊瑚礁算法的内部有性繁殖方式为遗传算法等经典算法传统意义上的变异方式,其受自身的影响较大,且变优趋势是随机的,不利于收敛.粒子群优化(PSO)算法是受到飞鸟集群活动规律性的启发,进而利用群体智能建立的一个简化模型,它通过追随当前搜索到的最优个体来寻找全局最优;而改进粒子群优化(IPSO)算法[14]是对PSO算法的更替方式进行了改进,具有向优收敛效果好、收敛速度快的优点.因此在CRO算法内部有性繁殖部分加入IPSO算法的改进以提高其向优收敛效果和收敛速度.本文受IPSO算法的启发,将内部有性繁殖公式(2)改为公式(4)和公式(5).

xi,j(t+1)=xi,j(t)+2r1[pbest(t)-xi,j(t)] ,

(4)

xi,j(t+1)=xi,j(t)+2r2[gbest(t)-xi,j(t)] .

(5)

改进后的珊瑚礁算法以自身最优珊瑚虫和全局最优珊瑚虫为参考对象,减少了差解的占比,并且设置了与代数相关的选择概率;前期有利于局部搜索,后期有利于全局搜索,不仅保持种群多样性,还提高了向优收敛速度.

2.2 无性繁殖方式改进

原无性繁殖部分是将当前所有珊瑚虫中最好的珊瑚虫按比例γ进行完全复制,产生幼虫.这样虽然增加了优秀珊瑚虫的比例,但使种群更容易陷入局部最优,不利于后期进一步搜索和提高精度.高斯变异是重点搜索原个体附近的某个局部区域,具有提高精度的优点;因此在CRO无性繁殖部分加入高斯变异,以提高搜索精度.本文受高斯变异[15]的启发,将无性繁殖方式改进为式(6).

xi=gbest,i+gbest,i·N(0,1) .

(6)

式中:i为比例为γ的高适应度珊瑚虫的序号;gbest, i表示从当前最优到次优依次排列的解;N(0,1)为正态分布.

改进后的无性繁殖部分不是单纯地复制最优珊瑚虫,而是按高斯变异的方式在最优解附近根据正态分布变异,这种变异方式在搜索后期种群趋于稳定后,仍可以对最优解进行微调,进一步提高搜索精度.

2.3 更替方式改进

原始珊瑚礁算法的更替方式为比较子代珊瑚虫与父代珊瑚虫的适应度大小,若子代适应度更好则代替父代,否则不代替.这种单纯的优势代替劣势,虽然使种群向优势种群收敛,但大大缩减了种群的多样性,未考虑到劣势种群的潜力,对于多峰值函数问题,极易陷入局部最优.模拟退火算法来源于固体退火原理,具有保留种群多样性、易于跳出局部最优的优点.因此在CRO更替方式部分加入模拟退火算法改进以保留其种群多样性,提高其跳出局部最优的能力.本文受到模拟退火算法[16]的启发对其进行改进,将更替方式改为式(7).

(7)

式中:fi为第i个珊瑚虫的适应度;i+1为第i个珊瑚虫的子代;T表示温度,温度随着代数的增长而下降,即T=0.7T.适用度的值越小,表示适应度越好,当子代适应度好于父代时,子代代替父代(即代替概率P为1);当子代适用度未好于父代时,以代替概率P代替父代.

改进后珊瑚礁算法的更替方式,不再是单纯地优势代替劣势,而是以一定的概率保留了适应度差的珊瑚虫,使其可以在下一代中作为父代产生新的子代珊瑚虫,增加了前期种群的多样性,避免种群因收敛过快而陷入局部最优;即使在后期种群陷入某个峰值,也有一定概率跳出局部最优.

改进珊瑚礁算法具体步骤如下:

①初始化:同CRO算法相同.

②外部有性繁殖和内部有性繁殖:外部有性繁殖方式与CRO算法相同,内部有性繁殖方式采用式(4)和式(5).

③更替机制:更替方式采用式(7).

④无性繁殖:无性繁殖方式采用式(6).

⑤毁灭机制:与CRO算法相同.

⑥进入循环,重复步骤②～⑤,直至满足终止条件,即达到最大迭代次数.得出最优解.

3 仿真实验与结果分析

3.1 实验参数设置

实验环境为64位操作系统,内存为4 GB,CPU为Inter(R)Core(TM)i5-3337U@1.80 GHz,程序采用MATLAB 2014a 编程实现.

将本文算法与原始珊瑚礁优化算法(CRO)[17]、高斯变异珊瑚礁优化算法(CRO(G))、柯西变异珊瑚礁优化算法(CRO(C))、高斯与柯西变异珊瑚礁优化算法(CRO(GC))[18]、粒子群优化算法(PSO)[19]、改进权重粒子群优化算法(IWPSO)、改进粒子群优化算法(IPSO)[14]、飞蛾扑火优化算法(MFO)[20]、多神经优化算法(MVO)[21]和正余弦优化算法(SCA)[22]在测试函数下进行比较.

在仿真实验中,统一设置种群规模为30,最大迭代次数为1 000.低维测试函数见表1,高维测试函数见表2.各算法均实验30次,求其平均值与标准差.针对15个低维和5个高维测试函数,算法结果见表3,对应的平均值曲线见图1.由于CRO(GC)已在文献[18]中被证明优于CRO(G)和CRO(C)，因此本文表中未列出CRO(G)和CRO(C)的数据.

3.2 实验结果分析

针对低维测试函数,从表3可以看出,ICRO在测试函数f1上要明显好于CRO,PSO,IWPSO,IPSO,MFO,MVO和SCA算法,并且从图1的f1可以看出其收敛速度极快,仅仅比CRO(C)差一点.在测试函数f2上,ICRO要明显好于CRO,IWPSO和MFO算法,比CRO(G),CRO(C)和MVO精确度更高,虽与SCA算法在平均值上相等,但标准差要比SCA算法更精确,比IPSO要稍差,但从图1的f2可以看出其收敛速度比IPSO要快得多,在第12代即达到稳定.而在测试函数f3上,虽然CRO(G),CRO(GC),IWPSO,MVO和SCA可以达到较好效果,CRO(C)能够达到8.3526E-15,但ICRO可以达到平均值和标准差都为0,且从图1的f3可以看出,ICRO稳定后在780代时跳出局部最优,进一步搜索最优值.针对测试函数f4和f9这种很难得到满意最优值的函数,ICRO对于f4可以达到3.986 6E-06,且从图1的f4可以明显看出ICRO曲线的波动,很好地展示了其跳出局部最优的能力,对于f9,甚至可以达到平均值与标准差都为0,且图1的f9进一步证明其跳出局部最优的能力.针对测试函数f5,PSO,IWPSO,MFO,MVO和ICRO都可以达到理论最优值-1.801 3,而ICRO算法与效果最好的IPSO和MFO达到了相同的平均值和标准差,且从图1的f5可以看出其收敛速度明显好于这两种算法,其在第10代达到稳定,而IPSO和MVO在100代左右才达到稳定.针对测试函数f6,虽然从图1的f6可以看到ICRO具有极高的收敛速度，但其精确度较差,与大部分对比算法一样未能达到1以下的效果,而IPSO可以精确到0.04.在测试函数f7,f11,f13,f14和f15上,ICRO算法精确度要明显好于其他算法.针对测试函数f8,ICRO可以达到0.039 51,且具有较高的收敛速度,比大部分算法要好,但SCA达到了1.525 1E-5.在测试函数f10上,虽然SCA达到了2.903 0E-245,但ICRO更加精确,达到了1.510 3E-251,且标准差为0.在测试函数f12上,ICRO能与对比算法中效果最好的IPSO达到相同的平均值,在标准差上稍微差一点,但从图1的f12可以看出其收敛速度明显好于IPSO.

表1 低维测试函数Table 1 Low-dimensional test functions

表2 高维测试函数Table 2 High-dimensional test functions

针对高维函数,从表3可看出,在测试函数f16上,ICRO也能达到最优的效果.在测试函数f17上,虽然CRO(G)可以达到7.401 5E-18,但ICRO在平均值和标准差上都达到0.且从图1的f17可以看出其收敛速度极快.在测试函数f18上可以看出,ICRO虽然收敛速度极快,但收敛精度效果有待提高.在测试函数f19上可以看出大部分算法都达不到一个较好的平均值,虽然CRO(C)平均值达到了5.199 3E-11,但ICRO可以在平均值和标准差上都达到0.在测试函数f20上,即使维度提高到1 000,ICRO仍然能达到算法中的最优效果8.881 8E-16.

总的来说,在所有测试函数中ICRO都具有极高的收敛速度,这要归功于ICRO在内部有性繁殖部分的改进,既保留了种群多样性,又极大地提高了收敛速度.在测试函数f1,f3,f4,f5,f7,f9,f10,f11,f13,f14,f15,f16,f17,f18和f20中,ICRO的精度都是最高的,这要归功于其无性繁殖部分的改进,大大提高了搜索精度.此外,在测试函数f3,f4和f9上,ICRO很好地展示了其跳出局部最优的能力,这要归功于其更替方式的改进,一定程度上丰富了种群的多样性,避免因种群收敛过快而陷入局部最优,即使其陷入了某个峰值,也有很高的概率跳出局部最优.

表3 测试函数的实验结果Table 3 Experimental results of test function

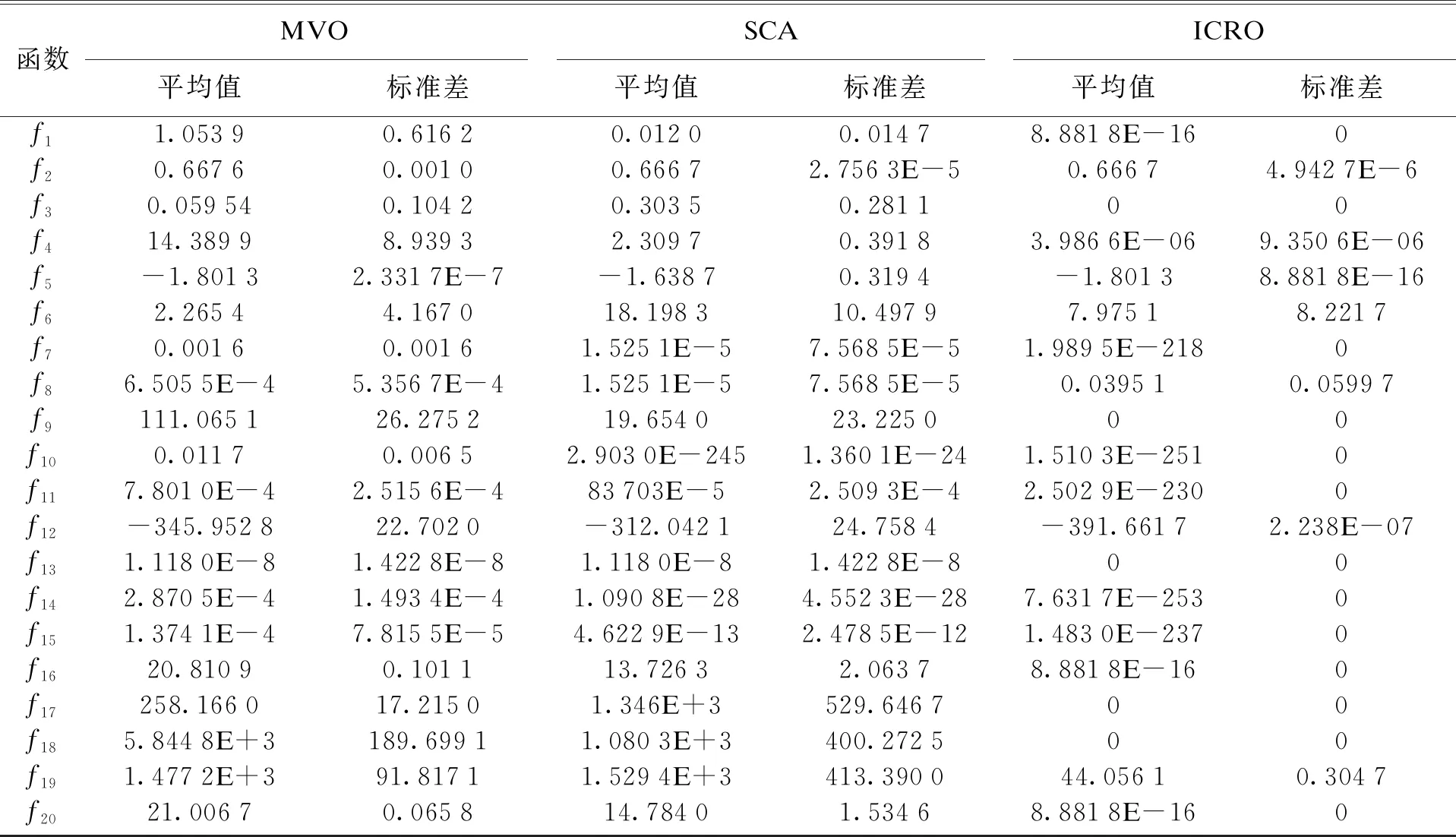
续表3

4 结 语

本文针对现有珊瑚礁算法存在的不足,提出了改进的珊瑚礁算法,在测试函数下证明了其相比其他算法可以更好地跳出局部最优,有效地改善了其原本易于陷入局部最优的缺点.相比其他算法,改进的珊瑚礁算法还具有更快的收敛速度和更高的搜索精度,即使在高维测试函数下仍然可以保持良好的性能.