基于MFE-GASVM的机载燃油泵故障诊断

戴邵武, 陈强强, 戴浩然, 邢 璐

(1.海军航空大学 岸防兵学院, 山东 烟台 264000； 2.中国人民解放军空军95596部队，河南 商丘 476000)

0 引言

随着武器装备制造工艺及设计理念的不断更新换代，武器装备的作战效能及作战时间都得到了很大程度的提高，同时现代战场对武器装备的可靠性及维修性也提出了更高的要求[1]。机载燃油泵系统主要为航空发动机提供指定的流量及压力状态下的燃油，为航空发动机源源不断的输送“血液”，是提高航空发动机作战能力并确定航空发动机作战效能稳定发挥的重要保障之一。机载燃油泵系统运行状态的优良与否，直接程度的关系着飞行任务及飞行安全[2]。在现代空战领域，机载燃油泵系统的故障可能导致航空发动机性能的不稳定，严重时甚至导致机毁人亡，造成不可估计的损失。因此，对机载燃油泵系统实现准确的故障诊断，对于提高机载燃油泵的可靠性具有重要意义。

对机载燃油泵系统中振动传感器所采集到的振动信号进行准确有效的故障特征提取，是实现机载燃油泵故障诊断的关键[3]。经典的非线性分析算法如混沌(Chaos)理论、Lyapunov算法等在非线性信号特征提取方面具有广泛应用[4]。李晓娟等[5]采用关联维数对飞参系统所记录的航空发动机状态参数进行分析，提取出反映航空发动机状态参数的特征信息，为航空发动机状态检测及视情维修提供了理论基础。经典的非线性算法在故障诊断领域具有重要作用，但在使用过程中存在着依赖数据长度、计算速度较慢、精度不高等不足[6]。而且随着机械系统复杂程度的不断提高，机载燃油泵等航空装备也逐步趋向于智能化、精密化、复杂化，所对应的振动信号也更加复杂，具有显著的非线性、非稳定性及非高斯型，为机载燃油泵的故障特征提取增加了难度。

为了弥补经典非线性算法的不足，熵(Entropy)理论逐渐在时间序列分析及故障特征提取中取得广泛的应用。Pincus等[7]最早提出近似熵(approximate entropy，ApEn)的概念，并将其用于医学方面的心电信号特征提取。但近似熵在使用过程中存在着自身匹配困难、过于依赖数据长度等不足；为了弥补近似熵在时间序列分析中的不足，在近似熵的基础上，Richman等[8]提出了样本熵(sample entropy，SE)的概念，用来衡量时间序列的复杂性。样本熵为非线性信号的特征提取提供了思路，但其不足之处在于所构建的函数基于单位阶跃函数(0～函数)定义样本熵值，无法准确判断样本类别。在此基础上，陈伟婷等提出了模糊熵(fuzzy entropy，FE)的概念[9]，通过采用模糊函数代替阶跃函数，解决了相似性度量的问题，并成功应用于机械系统故障诊断[10]。

机载燃油泵系统工作环境恶劣、制造工艺复杂，在运行过程中其振动信号具有强烈的复杂程度，且故障特征信息分布在多个尺度中，此时单一的FE熵值不足以完整概括其故障特征。为了弥补FE的不足并提高其特征提取能力，本文采用多尺度模糊熵(multi-scale fuzzy entropy，MFE)对机载燃油泵系统振动信号进行分析；将MFE提取的多尺度熵值作为特征向量输入至由遗传算法(genetic algorithm，GA)优化的支持向量机(support vector machine，SVM)中完成故障诊断。通过对机载燃油泵系统故障振动信号进行实验分析，结果表明MFE-GASVM算法可以有效的提取故障信息并完成不同故障类型的识别，是一种有效的故障诊断方法。

1 基于多尺度模糊熵的特征提取

1.1 模糊熵定义

1)连续性保证模糊熵的函数值不会产生数据突变；

2)指数函数的凸性质保证了向量本身自相似性值最大。

在理论分析中，对于长度为N的时间序列x(i)，其模糊熵求解过程定义如下。

步骤1：按顺序定义m维向量。

(1)

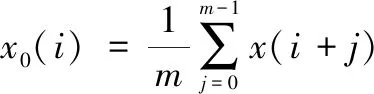
(2)

i,j=1,2,...,N-m,i≠j

(3)

(4)

步骤4：定义函数

(5)

步骤5：对维数进行m+1处理，在此基础上，重复步骤1～4，得：

(6)

步骤6：当N为有限长度时，根据公式(6)，可定义模糊熵为

FE(m,n,r,N)=lnφm(n,r)-lnφm+1(n,r)

(7)

1.2 多尺度模糊熵

多尺度模糊熵定义为不同尺度因子下的模糊熵值，通过引入多尺度粗粒化过程，实现不同尺度下的模糊熵值分析，多尺度模糊熵的计算方法如下[12]：

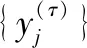
(8)

通过引入多尺度粗粒化过程，计算每个多尺度粗粒化序列的模糊熵值，并将其刻画成尺度因子的函数，所得多个尺度因子下的模糊熵值即为多尺度模糊熵。尺度因子的取值在一定程度上影响着多尺度模糊熵值分析。

2 基于GASVM的故障诊断算法

支持向量机作为经典的机器学习算法，在模式识别、时间序列预测等方面具有广泛的应用。在采用SVM进行机载燃油泵系统故障诊断的过程中，通过将非线性样本作为输入向量，并将其映射到高维特征空间中，然后在高维特征空间进行全局搜索以得到最优超平面，从而实现样本的分类[13]。在SVM实现分类的过程中，设样本的训练集为T={(x1,y1),(x2,y2),...,(xl,yl)}，其中xi∈Rn表示特征向量，yi表示类别标签(i=1,2,...,l)。

将SVM的寻找最优超平面问题转换为求解二次规划问题，可设置目标函数及约束条件为：

s.t.yi([xi,ω]+b)≥1-ξi

(9)

式中，〈·〉为内积形式，ω为权值向量，b为偏置；ξi表示松弛变量，在数值形式中为非负数，用来衡量数据点的偏离程度；C为惩罚参数，C的值越大表示对错误分类的惩罚越大。

根据Mercer定理，引入核函数概念，通过采用不同的核函数K(x,xi)，以实现非线性分类[14]。引入Lagrange算子ai，则最优分类的超平面决策函数可表示为：

(10)

使用SVM对经过多尺度模糊熵算法所提取出的机载燃油泵系统故障特征向量进行故障诊断时，核函数参数及惩罚参数对诊断结果影响较大，需要对其进行最优的自适应选择，以取得较好的故障诊断结果。GA算法是基于生物进化思想的全局寻优算法[15]。能够在搜索进程中自动获取和积累相关搜索空间知识，从而自适应的控制搜索过程以求得最优解。作为智能优化算法的代表，GA算法在工程应用中取得了广泛的应用。

3 MFE-GASVM故障诊断算法实现

综上所述，基于MFE-GASVM的机载燃油泵系统故障诊断方法为：

步骤1：对采集到的机载燃油泵系统振动信号进行分析，选择合适比例的训练集及测试集，为后续故障诊断提供数据准备；

步骤2：对机载燃油泵振动信号进行多尺度模糊熵分析，得到不同尺度因子下的FE熵值，将其作为实现机载燃油泵系统故障诊断所需的特征向量，构建合适的特征向量集；

步骤3：根据步骤1中得到的特征向量，构建SVM诊断模型所需的训练模型，其训练集的输入输出形式为：

Train=[MFE1,MFE2,...,MFEn,label]

(11)

式中，MFEi表示尺度为i下的模糊熵值；一般情况下，故障诊断所需的特征向量无需过多，较多的特征向量可能会造成特征数据的冗余及冲突，影响着故障诊断精度。本文参照文献[16]，选择前5个尺度下的模糊熵值作为特征向量，即n=5。表示SVM模型的标签值，不同的标签值对应不同的故障状态(如正常状态的标签值设为1)。

步骤4：针对步骤3中的SVM模型，采用GA算法进行核函数参数和惩罚参数的自适应选择，以建立最优的SVM训练模型，提高机载燃油泵系统的故障诊断精度。

步骤5：完成对机载燃油泵系统测试集的故障诊断实验过程，并对故障诊断结果进行分析说明，以论证算法的有效性。

4 实验分析

在某型机载燃油泵故障状态监测系统中，通过搭建机载燃油泵实验平台，在电机外壳上安装振动传感器并获取相应的振动信号。燃油泵的转速为5 600 r/min；传感器采样频率为6 kHz；选取样本长度为2 048；除正常状态(记为标签1)外，测量得到其他3种故障状态的振动信号，分别为扩散管损伤状态(记为标签2)、扩散管损伤与叶轮损伤并存状态(记为标签3)、渗漏状态(记为标签4)。每组状态共得到30组样本数据，选择前15组数据作为训练集(50%)，后15组数据作为测试集(50%)进行故障诊断分析。

然后，对样本数据进行多尺度粗粒化分析，选择前10个尺度下的模糊熵值进行多尺度因子刻画，为便于画图显示，每组状态选择2组样本数据进行展示，所得结果如图1所示。

图1 多尺度模糊熵

如图1所示，横坐标表示不同尺度因子，纵坐标表示在该尺度因子下对应的FE熵值。图1可表明：1)随着尺度因子的增加，FE整体呈下降趋势，这是由于多尺度粗粒化过程降低了原始时间序列的复杂程度，因此对应的FE熵值降低。2)label1状态下的多尺度模糊熵值在大部分尺度下均高于其他状态，这是因为正常状态下，传感器所接受到的轴承振动处于随机状态，所以在大部分尺度因子下振动的无规则程度较高，相应的自相似性较低，从而导致振动信号相对更加复杂。当出现故障状态时，振动信号的规则性增强，自相似性增加，导致模糊熵值降低。3)尺度因子为1时，即为不进行多尺度粗粒化过程，此时所得到的FE熵值即为原始时间序列对应的的FE熵值。

图1中的10个尺度因子仅为展示MFE随尺度因子变化关系，在进行机载燃油泵故障诊断分析过程中，不需要过多的特征量，参照文献[16]，仅选择前5个尺度因子下的FE熵值作为故障特征量并进行故障诊断。为了对比验证，首先采用单一尺度下的FE熵值作为GASVM特征量进行故障诊断，结果如图2所示。

图2 GASVM故障诊断结果(FE)

如图2所示，采用单尺度FE作为特征量时，故障诊断精度较低，仅为86.6667%(52/60)，此时所错分的8个样本将扩散管损伤状态(即标签2)误判为渗漏状态(即标签4)，误判数目比例达到53.33%，表明单尺度FE算法无法准确实现不同状态下的故障诊断。

采用本文的MFE-GASVM方法对相同的测试集进行故障诊断，特征量选择前5个尺度因子的FE熵值，所得结果如图3所示。

如图3所示，采用前5个尺度下的FE熵值作为特征量时，故障诊断精度为100%(60/60)，在图2中被误判的8个标签2样本均得到了准确的分类，实现了所有不同状态的故障识别。

图3 GASVM故障诊断结果(MFE)

5 结束语

本文采用MFE-GASVM方法对机载燃油泵系统振动信号进行分析，通过MFE提取不同故障状态振动信号的故障特征信息，解决了单尺度FE不足以完整概括特征信息的不足，有效提高了故障诊断精度，实现了对实验数据的故障诊断分析。实验结果表明：

1) MFE能够有效概括振动信号在不同尺度下的特征信息，相比单尺度特征提取方法而言，所得到的故障信息更加完整，有效提高了故障诊断精度。

2) 采用GA优化SVM的核函数参数及惩罚参数，可以提高SVM的自适应性，避免了参数选择问题，提高SVM的分类能力。