基于稀疏正则化的稳态热源识别*

潘天成，吕中荣，汪利

(中山大学航空航天学院，广东 广州 510006)

在实际工程中，存在着许多热现象，及时监测结构系统的温度，识别热源的位置和强度，对整个热传导系统的安全监测和温度控制具有重要意义。例如，通过测量核反应堆外部的温度，从而得到其内壁温度，实时监测和控制整个反应的温度；在电路中容易产生局部的热源，识别热源的位置可以用于对电路进行检修；航天飞机在进入大气层时，经常会产生气动加热，航天器的局部结构产生热源，因此根据局部温度场来识别热源的位置和强度就显得尤为重要。热源识别属于热传导反问题的研究领域[1]，目的在于识别热源的位置和强度，及时掌握系统中热源的属性。研究表明，热源识别问题一般是非适定的[2]，导致识别结果对温度测量误差十分敏感。

实际上，热源识别的研究主要分为两类：一是给定热源的位置或者空间分布，识别热源的强度；二是同时识别热源的空间位置和强度。过去几十年，很多学者已经对热源识别问题做了大量的研究。为求解此类非适定问题，BECK提出在最小二乘方程中添加正则化项求解，发展并使用了Tikhonov正则化方法。在一维的热传导问题中，BLACK WELL提出了序列估计方法[3]。HUANG等通过共轭梯度法来研究了一维和二维模型中的一个或两个点热源的强度识别问题[4]。但是由于算法迭代的特性，计算时间比较长。GENG等采用变分迭代算法求得抛物型热方程无离散化问题的数值解并确定热源的强度[5]。NETO等完成了矩形域内特定位置的线热源随时间变化的强度识别[6]。LI等提出了一种并行蚁群的优化算法来识别二维域中的一个点热源[7]。第一类热源识别的研究工作比较多，但对于第二类热源的识别研究却十分有限。主要难点在于测量得到的温度与热源强度和位置之间呈复杂、难以显式表达的非线性关系，而且在有限元的框架下，测量数据量将小于未知参数数目，导致问题的严重非适定性。幸运的是，稀疏正则化可以很好地解决这一问题[8-9]。

本文将提出一种新的方法来研究热源识别第二类问题。考虑到点热源在空间上的分布是稀疏的，引入稀疏正则化[10-12]来对目标函数进行约束, 并且采用交替优化方法[13]分别对温度和热源两个分离的变量进行迭代求解。在寻求正则化参数的过程中，提出了阈值法。本文所提算法能快速准确地识别热源位置和强度，这给实际工程的应用提供了一定的参考。

1 稀疏正则化目标函数建立

1.1 热传导问题有限元格式

考虑一个包含边界∂Ω的二维域Ω的热传导问题，一般的控制方程为

+Q(x,y,t),

x,y∈Ω,t≥0

(1)

其中，x,y是笛卡尔坐标，T为温度，α为不随时间变化的热传导率，Q是热源项，本文主要考虑为点热源的情形。

边界条件为

=h(Te(x,y,t)-T(x,y,t))

在∂qΩ边界上T(x,y,t)=g(x,y,t),在∂TΩ边界上

∂qΩ∪∂TΩ=∂Ω,

∂qΩ∩∂TΩ=φ,∂TΩ≠φ

(2)

其中，nx、ny分别是二维域边界的法向方向余弦，h是对流换热系数，Te(x,y,t)是周围的环境温度，∂TΩ和∂qΩ分别为本质边界和对流边界，g(x,y,t)是在本质边界∂TΩ给定的温度分布。

初始条件为

T(x,y,0)=T0(x,y)

(3)

其中，T0(x,y)为二维域内的初始温度分布。

+Q(x,y,t)=0,

x,y∈Ω,t≥0

(4)

有限元方法是求解热传导问题(1)-(4)的有效数值方法，将二维域Ω划分为有限个微小的单元dΩ，通过分段线性插值得到的有限元形函数，可以将域内的温度用各节点的温度表示。那么，稳态情况下的有限元格式如下：

(5)

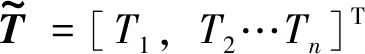
1.2 建立目标函数

(6)

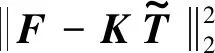
(7)

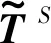
1.3 稀疏正则化

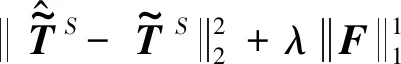
(8)

其中，λ≥0是一个正则化参数。至此，基于稀疏正则化的有限元格式稳态热源识别目标函数已经建立。

2 交替优化方法

2.1 交替优化方法求解目标函数

2.1.1 温度恢复步 完整的温度数据从测量得到的温度中得到恢复。

(9)

+(F(k-1))TF(k-1)

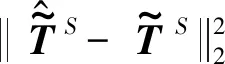
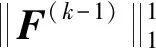
+(F(k-1))TF(k-1)

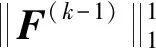
其中，公式(10)中的上标S和U分别对应测量的节点和未测量的节点，上标US对应耦合的部分，I是一个单位矩阵。因此可以得到公式(9)的解，如下

2.1.2 热源识别步

从恢复得到的完整温度数据中识别热源位置和强度，如下

(12)

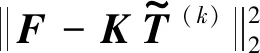
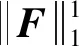
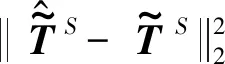
(13)

其中，(ν)j表示向量ν的第j个分量。显然，问题(13)是具有显式解。因此，热源识别步，即公式(12)的解为

(14)

可以发现，公式(14)容易得到稀疏正则化目标函数的最优解，而且目标函数是解耦的，无需迭代。进一步的研究表明，稀疏正则化参数λ可能会对热源的强度识别造成一定的偏差，因此应避免，本文对公式(14)进行了修正，消除λ对识别的热源强度的影响。

=fm(λ;aj)

(15)

关于λ的选取将在接下来进行讨论。

2.2 阈值法寻求正则化参数

在执行每一热源识别步之前，都必须选取一个合适的正则化参数。根据公式(15)，可选取一个阈值集τ。

τ={λjcr:=2|aj|,j=1,2,…n}

(16)

当λ≥λjcr时，公式(15)的解为0，即表示在第j个节点内部没有点热源存在；λ<λjcr时，结果表明点热源在相应的节点内部。将阈值集进行降序排序

(17)

那么就可以通过阈值法来选取一个正则化参数，基本算法如图1所示。其中，lmax和γ是两个阈值参数，lmax表示点热源存在的最大个数；γ是一个判别比，通常在lmax比较小的情况下，取值较大。

图1 阈值法确定正则化参数流程图Fig.1 The flow chart for determining regularization parameters by threshold setting method

3 数值算例

3.1 模型建立

本文考虑一个二维稳态的数值算例。通常，测量的温度是从有限元模拟并添加一定的噪声得到。在稳态情况下，噪声施加下

(18)

其中，Tj是从公式(5)求得的在第j个节点的温度数据。ε是噪声水平，一般为0%、2%、5%等等。r是一个标准正态分布的随机数。

如图1所示，薄板为铝合金材料，长和宽均为0.5 m，密度ρ=2 787 kg/m3，比热容c=883 J/(kg·K)，热传导率α=194 W/(m·℃)， 对流换热系数h=10 W/(m2·K)，环境温度为0 ℃，一个或多个热源在薄板的内部。每个热源的面积为0.004 m×0.004 m，相对于板的面积是非常小的，因此可以看作是点热源。

薄板的有限元单元和节点信息，如图2所示。

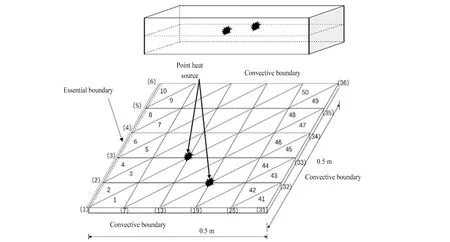
图2 二维稳态模型图Fig.2 Two-dimensional steady-state model

考虑以下几种工况，来验证所提方法的有效性和准确性，热源的强度Q15=1.2×106W/m2，Q20=1.0×106W/m2。

3.2 热源识别结果

在识别表1四种工况的过程中，考虑噪声的随机性，进行蒙特卡洛(monte carlo)试验，每种工况取100组数据进行研究，最后取其均值和标准差作为识别结果。在算法实现过程中，阈值法选取的参数分别为lmax=4,γ=5,β=1×106，fb的值则在每一次迭代的过程中选取矩阵ASS的2范数，即fb=norm(ASS)。

四种工况稀疏正则化与无正则化的识别结果如图3-6所示，每种工况第20节点内部的热源强度识别结果及相对误差如表2所示。在无噪声的情况下，目标函数中有稀疏正则化与无正则化均能准确识别热源的位置和强度，无正则化识别的强度误差也为0。当有噪声水平的时候，稀疏正则化的识别结果明显比无正则化的结果要好，而且能保证解的稀疏性，而无正则化的时候不能保证。同时发现，噪声水平的提高，蒙特卡洛实验得到的热源识别标准差也会增大，但不影响热源的定位。工况4表明，仅通过边界点的测量，本文所提方法也能准确定位结构内部的热源，且识别的强度误差不大，误差为3.62%，而无正则化的算法甚至无法准确定位。在测量数据量比较少的情况下，稀疏正则化的优势明显地体现出来了。

图3 工况1有无稀疏正则化识别结果对比Fig.3 Identified results without and with regularization for scenario 1

表2 第20节点热源强度识别结果Table 2 The identified results of heat source strength at 20th node

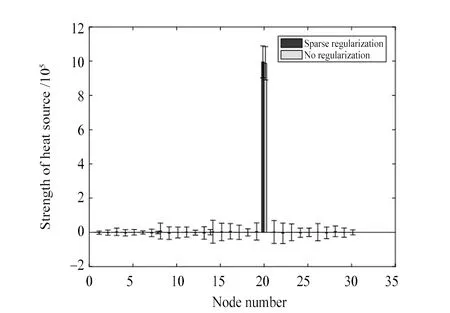
图4 工况2有无稀疏正则化识别结果对比Fig.4 Identified results without and with regularization for scenario 2

图5 工况3有无稀疏正则化识别结果对比Fig.5 Identified results without and with regularization for scenario 3

图6 工况4有无稀疏正则化识别结果对比Fig.6 Identified results without and with regularization for scenario 4

4 结 论

本文考虑到点热源在空间分布上的稀疏性，将稀疏正则化与交替优化方法结合，提出了一种新的热源识别方法，很好地克服了热源识别非适定性的问题。数值算例的结果表明：该方法能同时识别热源的位置和强度，稀疏正则化能加强解的稀疏性，具有较好的抗噪性，并且交替优化方法的求解和阈值法寻求正则化参数使得识别快速准确，甚至仅通过边界的测量也可识别内部的热源，这给实际工程提供了一定的参考意义。