基于进化计算的特征选择方法研究概述
王艳丽,梁 静,薛 冰,岳彩通
(1.郑州大学 电气工程学院,河南 郑州 450001;2.新西兰惠灵顿维多利亚大学 工程与计算机学院,新西兰 惠灵顿 6140)
0 引言
随着大数据时代的到来,数据挖掘和机器学习成为研究热点,并受到了国内外研究人员的广泛关注。特征选择(feature selection, FS)是从一组初始特征中挑选出一些具有代表性的特征以降低特征空间维数的过程,是数据挖掘和机器学习的关键问题之一。对于数据挖掘和机器学习,一个好的学习样本是训练分类器的关键,样本中是否包含有不相关或冗余特征直接影响着分类器的性能。特征选择的目的是寻找解决问题所必须的、足够的最小特征子集。通过从原始特征集中剔除不相关和冗余特征以减少数据的维数,加速学习过程,简化学习模型和提高学习算法的性能[1]。有效的特征选择方法是找到一个最优的特征子集的关键。
现实中的数据集通常由一组特征描述,这些特征包含许多信息,但也引入了冗余和噪声。随着数据维度的增加,搜索空间增大,选择最优特征子集变得尤为困难。比如对于一个有n个特征的数据集,特征子集的个数就有2n个[1]。随着问题复杂性的增加,许多领域数据的特征维度都在逐渐增加,特征选择变得更具挑战性。在大多数情况下,穷举搜索给定数据集的最优特征子集几乎是不可能实现的。目前已有许多搜索技术应用于特征选择,如完全搜索、贪婪搜索、启发式搜索和随机搜索[1-2]。现有的搜索技术在特征选择上取得了较大的成功,但大多数方法容易陷入局部最优,并且计算成本较高[3]。因此,需要一种有效的全局搜索技术来更好地解决特征选择问题。
进化计算(evolutionary computation, EC)算法通过模拟自然界生物进化机制,在一些可行解组成的种群中,通过迭代进化寻求最优解。EC技术因其强大的全局搜索能力和潜力备受研究者的关注,近年来更是广泛应用于特征选择问题。然而,现有的文献对近些年EC在特征选择上的应用缺乏全面而系统的讨论。基于此,笔者对EC在特征选择上应用的相关文献进行了分析和总结,给感兴趣的研究人员提供一些参考。
1 特征选择的基本框架
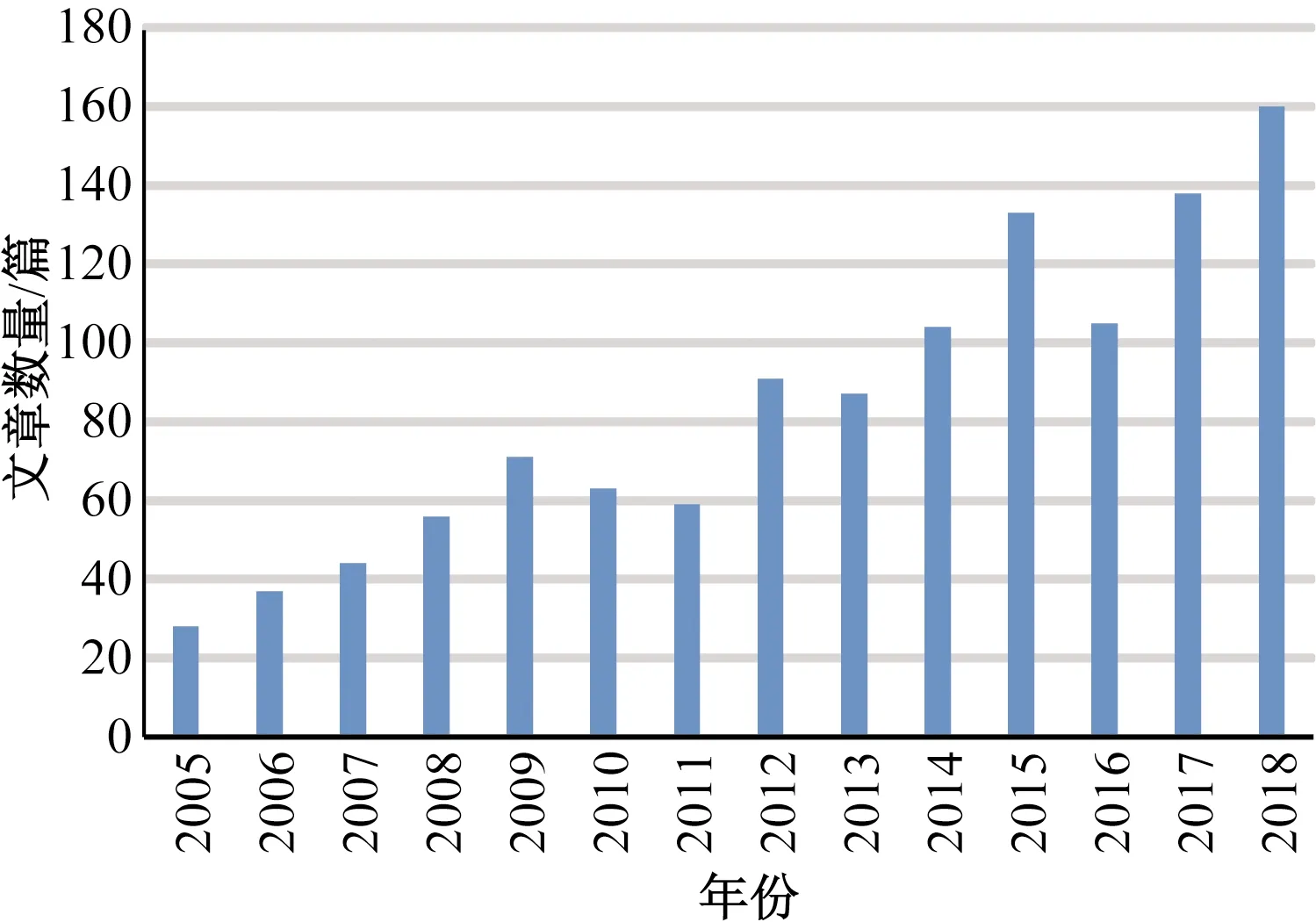
特征选择是从数据集特征的所有组合组成的搜索空间中选择相关特征子集的过程[2]。迄今为止,许多研究者从不同的角度对特征选择进行定义。Koller 等[4]从传统的角度定义,给定n个原始特征,特征选择的任务是从所有大小为m的特征子集中(m 图1 特征选择的基本框架 从图1可以看出,在特征选择中,搜索机制和评价准则是影响最终特征子集质量的重要因素。 传统的特征选择方法可以分为:过滤式(filter)[7]、封装式(wrapper)[8]和嵌入式(embedded)[9]。过滤式方法先对数据集进行特征选择,然后再训练学习器,一般直接采用所有训练数据的统计性能评估特征,速度快,但缺少学习算法的引导导致分类性能相对较低。封装式方法利用学习算法的训练精度作为特征子集的评价准则,偏差小,但是计算量大。嵌入式方法是将特征选择过程嵌入到学习过程中,特征选择过程和学习器训练过程同步进行,因此花费时间大幅减少,但不适合处理含有大量噪声特征的数据。集成(ensemble)[10]是近几年发展起来的一种新的学习方法,应用于特征选择问题,目的是获取多个最优特征子集,并聚合基于多个最优特征子集的学习结果。 与传统方法相比,基于种群的EC算法能并行搜索多个解,利用计算机技术自动搜索解决方案,不需要问题领域先验知识。基于这些优点,EC在特征选择上获得较大成功[11]。EC在特征选择上的应用研究始于1990年左右,但是自2007年以来,随着许多领域的特征数量逐渐增多,EC技术以其强大的全局搜索能力而受到特征选择领域的广泛关注。如图2所示。 图2 进化计算用于特征选择的论文数量 图2显示EC算法在特征选择上应用的论文数量(数据来源Web of Science,2018.12),这表明自2007年以来,进化计算在特征选择上的应用呈整体增长趋势。笔者对进化计算在特征选择上的代表性研究工作进行讨论,并对进化计算在单目标、多目标特征选择上的研究工作分别进行详细的介绍。 特征选择的目的是通过从原始特征集中删除不相关和冗余的特征找到解决分类问题所必需和充分的最小特征子集。特征选择有两个主要目标:最大化分类性能和最小化选择特征的数量。 实际操作过程中,常用问题解的编码有连续和二进制两种表示方法,具体如下:连续表示指一个含有n个实数的向量,其中n是数据集中可用特征的个数或搜索空间的维数。每个个体i的位置向量值.id与设定的阈值θ进行比较。如果.id>θ,则特征d被选择;否则,特征d未被选择。每个个体采用二进制字符串“0”和“1”表示,“1”表示个体对应的特征被选择,“0”表示未被选择。 进化算法包括遗传算法(genetic algorithms, GA)、遗传规划(genetic programming, GP)、进化规划(evolution strategies, ES)和进化策略(evolution programming, EP)等。目前,遗传算法和遗传规划被广泛应用于特征选择中,以寻找最优特征子集。 2.2.1 遗传算法 GA算法[12]是模拟达尔文生物进化论的自然选择和自然界生物进化过程演化而来的随机搜索最优解的方法。Siedlecki等[13]采用GAs解决特征选择问题,首次把EC技术应用到特征选择问题中。为了提高算法性能,研究者对GAs进行了许多不同的改进,主要集中在搜索机制、个体表达和评价机制等方面。 传统的GAs由于遗传算子简单,降低了种群的多样性。当搜索空间很大时,GAs容易快速收敛而陷入局部最优。为了避免这一问题,Li等[14]提出一种多种群GAs的特征选择方法,即相邻种群通过共享两个个体来交换信息,以提高种群的搜索能力。此外,对每个种群中的最优个体进行局部搜索,进一步提高算法性能。但是该方法仅在特征维数小于60的数据上是有效的。Lin等[15]提出了一种新的基于GAs的特征选择方法,该方法首先利用先验知识对相似特征进行分组,并对同一组中的所有特征进行排序,然后采用GAs从每个组中搜索出最优特征子集。近年来,GAs也被应用在分层特征空间中选择特征[16]。该算法提出了两种新的变异算子处理分层空间中的冗余特征。最近基于GA的特征选择方法被广泛用于解决实际问题[17-18]。 Hong 等[19]提出一种二进制向量表示每个个体,首先二进制位预先定义的小数被转换为整数,表明对应的特征被选择与否。该算法有效地降低数千特征的高维数据集上GA搜索空间的维度。同时,在算法中引入“透明适应度共享”伸缩机制以避免GA 在搜索过程中出现早熟。通过分界线的动态变化来增加其他个体的选择机会,并打散个体的分布以保持种群的多样性。Chen等[20]提出一种改进的二进制表示方法,该方法包括两部分:第一部分被转换为整数,表示被选择特征的数量;第二部分显示哪些特征被选择。该方法的缺点是需要预先定义特征的数量,但可能不是最佳大小。针对这一问题,Yahya等[21]开发了一种长度可变的表示方法,每一个个体只显示所选择的特征,并且不同的个体可能具有不同的长度,提出了一种新的遗传算子来处理长度可变表示问题。 OA Silva 等[22]将分类精度和特征个数聚合成一个适应度函数。Winkler 等[23]考虑特征个数、分类性能、分类特定精度以及利用所有初始特征的分类精度等提出了几个适应度函数。Sousa 等[24]利用贝叶斯分类器接收工作特性曲线下面积作为适应度函数。 2.2.2 遗传规划 GP算法[25]是一种基于种群的进化计算算法,在特征选择中,GP算法具有灵活的表示形式,每个个体表示为一棵树,每棵树的所有叶节点都是原始特征,但只有一个叶节点特征被认定是选择的特征。 Sherrah等[26]首次将GP算法用于特征选择问题,该算法采用广义线性机作为分类器来评价所选特征的适应度。随后,Neshatian等[27]提出一种基于GP的封装式特征选择方法,采用改进的贝叶斯算法进行分类。该算法采用位掩码编码表示特征子集,算子集作为基本函数,利用GP将特征子集和算子集进行组合,获得最优特征子集。Hunt等[28]提出一种新的GP超启发式特征选择方法,开发两个去除和添加特征的函数算子。Viegas等[29]提出一种处理平衡和不平衡数据的策略,GP算法中的每个内部节点表示一个集合算子,每个叶节点表示一个原始特征,每个树的输出是一组特征。结果显示,该算法在不降低分类性能的前提下,可以有效地减少生物数据集98%的特征。 进化算法应用于特征选择问题已有30多年的历史,并在数百个特征问题上显示出了较好的性能。然而对于数千特征的问题,进化算法的效果并不是很理想。因此,使用进化算法来处理这一问题,需要一种新的表示来减少搜索空间的维数。遗传算子的设计,如交叉和突变,提供了辨别好的特征组及组合或调整互补特征以找到最优特征子集的机会,但这是一项具有挑战性的任务。 群集智能算法是人们受自然规律或生物界规律的启发,模仿某些规律而设计的求解实际问题的一类算法,它将复杂任务交给群体中大量的个体合作完成,具有概念简单、实现方便的特点。基于这些优点,群集智能算法求解特征选择问题受到了国内外研究者的广泛关注[11]。群智能算法包括蚁群优化(ant colony optimization, ACO)、粒子群优化(particle swarm optimization, PSO)、差分进化(differential evolution, DE)、人工蜂群算法(artificial bee colony, ABC)等[30]。 Xue等[31]在PSO搜索过程中设计了新的初始化策略模拟典型的前向和反向特征选择方法。结果表明,新的初始化策略显著提高PSO特征选择的性能。PSO中开发新的个体表示用于特征选择的工作较少,研究者主要对典型表示进行微小的修改,同时用分类算法进行特征选择和参数优化,工作主要集中在对支持向量机核函数中的参数进行优化[32-35]。PSO中新的个体表示长度等于特征总数,主要有3种不同编码方式:连续编码[32]、二进制编码[33]和二进制和连续编码的混合[34-35]。PSO最初被提出用于连续优化,因此连续编码比其他两种编码方案具有更好的性能。 Vieira等[33]提出新的PSO粒子表示方法,并同时进行特征选择和SVM核参数优化。该方法中每个粒子对应一个初始特征或内核参数,表示长度等于特征个数和内核参数个数的和。结果显示,所提算法比其他二进制PSO特征选择算法具有更好的分类性能,选择的特征子集远小于GA算法。Lane等[36]提出了采用PSO和统计聚类方法解决特征选择问题,将来自于相同簇的特征分配到一起,然后从每一簇中仅选择一个特征,该方法显著减少了所选特征的数量。随后,Lane等[37]进一步采用高斯分布从每个簇中选择多个特征改进了算法,提高了分类性能。Nguyen等[38]提出每一个个体的维度由期望的最大特征数目确定,该方法确定的个体维度远远小于典型解的代表维度,但是难点在于如何确定期望的特征数量。Tran等[39]提出粒子长度可变表示,从而定义了较小的搜索空间,提高了PSO算法的性能。利用变长机制,PSO可以跳出局部最优,进一步缩小搜索空间。 早熟收敛是PSO面临的一个典型问题,容易使种群陷入局部最优。为了避免这一问题,Chuang等[40]提出在有限次迭代中,最佳适应度值不变,将gbest置零的重置机制。随后,Tran等[41]将gbest重置机制与pbest局部搜索结合,通过被改变的特征来计算适应度,加快局部搜索中的评价。Cheng等[42]在所提的PSO算法中,去掉了gbest和pbest,以避免PSO的过早收敛。通过粒子之间的竞争,获胜者直接进入新的种群。失败者向获胜者学习,根据获胜者的位置更新它们的位置,然后进入新的种群。该算法被称为竞争群优化算法,适用于大规模优化问题。随后,Gu等[43]将这种改进的PSO算法应用于特征选择问题。 适应度函数在PSO特征选择中起着重要的作用。对于过滤式方法,适应度函数通过使用不同的度量方法确定。而封装式方法,许多现有的工作使用分类性能作为适应度函数[3,40],导致特征子集相对较大。然而,大多数适应度函数采用不同的方式将分类性能和特征数相结合组成为一个适应度函数[34,44]。但是,如果没有先验知识,很难预先确定它们之间的最佳平衡。多目标特征选择可以同时优化这两个目标以获得一组折中解,从而有效地解决这一问题。 2008年以来DE一直被应用于解决特征选择问题。大部分工作主要集中在改进DE的搜索策略和表示方法。Khushaba等[45]提出将DE用于搜索ACO得到的特征子集的最优解的混合特征选择方法。Ghosh等[46]提出采用自适应DE算法用于生成特征子集。随后,Khushaba等[47]将每个个体作为一个浮点数向量,并预先定义向量的长度,提出一种新的编码方案。此外,研究表明,DE在大规模优化方面也取得了成功[48],但对于特征数量较多的高维问题,还面临一些困难。 Hancer等[49]将基于相似性的进化搜索机制引入到现存的二进制 ABC 版本中,提出了新型二进制 ABC算法用于特征选择问题。模因算法将基于种群的搜索和局部搜索结合,为封装式和过滤式方法提供好的机会。因此,在大多数模因特征选择方法中,封装式特征选择采用进化计算技术,过滤式特征选择采用局部搜索算法。 总之,群集智能算法在特征选择方面得到了迅速的发展。然而,作为一种种群优化方法,群集智能用于特征选择效率是有限的。开发新的PSO算法,特别是新的搜索机制、参数控制策略以及大规模特征选择的表示,仍然是一个有待解决的问题。 协同进化(cooperating coevolution,CC)是进化计算领域的一种技术,从分治策略发展而来,其思想是首先将复杂的问题划分成多个简单子问题,然后对每个子问题应用算法进行求解,最后将子问题的解合并得到原问题的解。协同进化策略可以嵌入到多种进化算法中,具有很好的鲁棒性,已成功应用到许多大规模的组合问题中[50]。Derrac等[51]提出一种基于3种群遗传算法的协同进化特征选择算法。算法将特征选择和实例选择同时放在一个过程中,减少了计算时间,对具有大量特征及噪声实例的数据集效果显著。随后,Derrac等[52]进一步采用协同进化,对特征和实例进行数据降维,提出了一种最近邻分类特征选择和实例选择的进化模型。Ebrahimpour等[53]提出一种新的基于全局搜索(利用分治策略)的特征选择方法。该方法利用协同进化概念,在特征维度上以随机方式垂直划分数据集,使用过滤式准则以二元引力搜索算法搜索解空间。 在实际问题中,决策者希望得到多个全局或局部最优解,必要时可以在多个最优或次优解之间快速切换以保证系统正常稳定运行[54]。这类需要同时保留多个全局最优或局部最优解的问题属于多模态优化(multimodal optimization, MO)问题[55],如机器学习中的分类问题[56]、特征选择问题[57]等。 Kamyab等[58]研究了多模态优化技术在特征选择问题中的应用效果。提出了基于动态适应度共享(dynamic fitness sharing, DFS)、局部最优粒子群算法(local best PSO)和GA_SN_CM等现有进化算法的二进制版本,用于从多个基准数据集中选择合适的特征。特征选择本质上是一个高维优化问题,需要一个具有较高探索能力的求解器。另一方面,如果可以为问题提供可选的最优解方案,则根据问题领域的成本和限制,实现阶段会变得更具选择性。MO方法具有较强的探索能力和解的保存能力,能够在一次运行中找到多个合适的解。因此,MO方法可以被认为是寻找适合特征选择问题的特征子集的有力工具。 在许多实际问题中,需要同时优化两个或两个以上相互冲突的目标,优化其中一个目标值,会导致其他目标值的恶化,这类问题被称为多目标优化问题[59]。对于多目标优化问题,无法找到单个解使它的每个目标都达到最优。在这种情况下,进化算法能够帮助决策者找到多个目标之间最好的折中解集。 GA在实现多目标特征选择方面也得到了广泛的应用,但大多数都是基于非支配排序的GA II(NSGA-II)或其变体[60-62]。Mukhopadhay等[60]利用NSGA-II和支持向量机(SVM)提出识别微小RNA标记物的多目标的特征选择方法。Vignolo等[63]应用多目标遗传算法(MOGA)选择人脸识别中最相关的一组特征。通过对多个可行选择空间的探索,使特征子集的基数最小化,同时最大化特征子集的识别能力。结果显示,MOGA得到的解选择的特征较少,但精度与单目标GA相近。Neshatian等[64]针对二分类问题,提出基于GP的多目标过滤式特征选择方法。与大多数只能测量单个特征与类标签相关性的过滤式方法不同,该算法能够发现特征子集和目标类别之间的隐藏关系,从而获得更好的分类性能。 近年来,DE也被应用于多目标特征选择[65]中,并将非支配解排序应用到种群搜索中,研究者提出的多目标方法在分类性能和特征个数上都优于单目标方法所获得的特征子集。Hancer等[66]将ReliefF和FisherScore两个过滤式准则结合起来作为排序度量标准,归一化交互信息作为相关性度量标准,并将这两种度量方法视为两个相互冲突的目标。结果表明,该算法获得较小的特征子集,且分类精度高于使用所有特征。DE虽然成功应用于解决特征选择问题,然而与PSO相比,应用DE的特征选择算法文章仍然较少。此外,研究显示,DE在应用于高维问题时还面临一些困难[67]。 Xue等[68-69]首次将MOPSO应用于特征选择上,把分类性能和特征数量作为多目标优化问题的目标函数进行求解,并将连续和二进制PSO算法在多目标特征选择上的性能进行了对比。结果表明,MOPSO在特征选择问题上优于NSGA-II等。Xue等[70]以最小化特征数量,最大化所选特征和类标签之间的相关性为目标,提出基于MOPSO的过滤式特征选择方法。结果显示,与单目标特征选择方法相比,该算法具有更高的分类性能。随后,Nguyen等[71]通过引入插入、删除和交换局部搜索机制提出了基于改进多目标PSO算法的特征选择方法。该算法可以选择数量较少的特征,并获得很好的分类性能。 目前大多数的多目标特征选择算法采用基于帕累托(Pareto)支配的算法,这些算法通常集中在Pareto前沿的中心。针对这一问题,Paul等[72]将类间距离和类内距离度量作为两个相互冲突的目标,利用模糊规则从最终的Pareto前沿提取单个解,提出一种MOEA/D过滤式特征选择算法。 在EC技术中,GA算法的多目标算法是最受欢迎的,但是这些工作只是简单地应用GA而不考虑特征选择的特点[11],因此对GA进行多目标特征选择还需要进行深入的研究。 近年来,进化计算技术较为广泛地应用于特征选择并取得了较大的成功。特征选择也已成为EC的一个重要应用领域。通过归纳已有研究工作,将未来EC技术在特征选择上的研究问题归纳如下。 (1)随着数据规模越来越大,许多领域的特征数量达到数千甚至数百万,增加了计算成本。然而,仅靠通过增加计算能力是无法解决的,这就需要先进的搜索机制。现有的基于进化计算的大规模特征选择方法大多采用两阶段方法,第一阶段采用度量方法对单个特征进行相关性评价,然后根据相关性值对其进行排序。只有排名最靠前的(更好的)特征才会被用作第二阶段的输入,进一步从中选择特征。但是,第一阶段删除了排名较低的特征,并未考虑它们与其他特征的交互。为了解决这一问题,需要新的搜索算法和新的评价措施。 (2)大多数特征选择方法由于涉及大量的评价,计算成本较高,是进化计算在特征选择上的一个关键问题。为了降低计算成本,需要高效搜索技术和快速评估措施。目前的方法中,评价过程占据了大部分的计算成本。因此,快速评价准则比搜索技术影响更大。进化计算的可并行性适合于网格计算、图形处理单元和云计算,可以用来加速评价过程。 (3)特征选择本质上是组合优化问题,随着特征维数的增加会导致“维数灾难”,传统的穷举法容易陷入局部最优,因此需要一种强大的全局搜索技术。EC算法是一种随机方法,使用不同的起始点可能产生不同的解,即使解的适应度值相同,也可能选择不同的个体特征。这就要求新的搜索机制应具有稳定性。然而,算法的稳定性不仅涉及适应度值的差异,还涉及所选特征的一致性。因此,提出新的高稳定性的搜索算法也是一项重要的任务。 (4)评价指标构成的适应度函数,在很大程度上影响了计算时间、分类性能和搜索空间的分布,是特征选择的关键因素。封装式和过滤式的大部分计算时间都用在评估过程中。目前有一些快速评估方法,如交互信息,但它们都是单独评估特征,而不是一组特征。如果忽略特征之间的交互会导致特征子集具有冗余性并缺少互补特征,从而无法在大多数领域中实现最佳分类性能。特征交互是一项复杂且具有挑战性的任务,目前在这方面的工作还很少。 (5)大多数进化计算方法中,传统表示方法在特征选择问题上存在很大的搜索空间。一个好的表示方法可以减少搜索空间的大小,从而有助于设计新的搜索机制来提高搜索能力。目前的表示方法通常只反映是否选择了某个特性,而不显示特征之间的交互信息。如果表示能够反映特征组的选择或删除,则可以显著提高分类性能。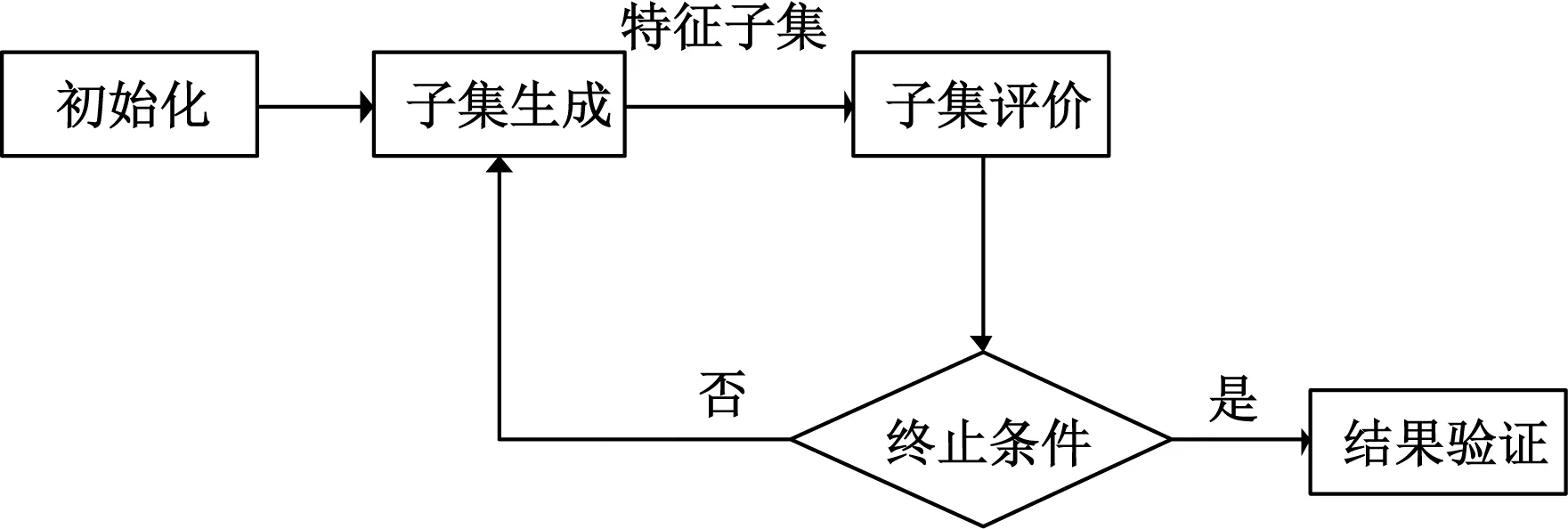
2 基于进化计算的单目标特征选择
2.1 特征选择的目标和个体表达
2.2 基于进化算法的特征选择
2.3 基于群集智能的特征选择
2.4 基于协同进化的特征选择
2.5 基于多模态的特征选择
3 基于进化计算的多目标特征选择
4 总结与展望

