架空导线径向温差及允许载流量研究

张 猛，梁 任，赵桂峰

(郑州大学 土木工程学院，河南 郑州 450001)

0 引言

近年来，随着我国经济的快速发展，高峰期供电紧张的问题日益突显。解决该问题的方法，除了架设新的输电线路外，实施既有线路动态增容又有技术改造的方案是另一有效途径，这势必会使架空导线长期处于高温负荷状态，当导线温度超过其长期运行允许温度时，可能会引起导线强度损失、连接点氧化和对地安全距离降低，这给线路的安全带来严重隐患。现有的动态增容方法常采用非接触式红外测温技术，以测得的导线表面温度作为其允许温度[1-2]，据此对线路载流量进行实时调控。该法对导线运行时的温度场考虑不足，忽略了导线径向温差对其载流量的影响，有可能得到偏于不安全的调控结果。

实际架空导线多采用钢芯铝绞线，由于内外层线股接触和散热条件不同，使得导线运行时存在径向温差。我国110～750 kV架空输电线路设计规范[3]规定：验算导线允许载流量时，钢芯铝绞线和钢芯铝合金绞线的允许温度宜取70 ℃。该规定虽然给出了允许温度限值，但并未明确其含义。事实上，当考虑导线径向温差时，其允许工作温度的不同定义对于其允许载流量亦有较大影响。因此，准确分析架空导线的径向温度场，进而对其允许温度限值的定义进行讨论，对于确定导线最大载流量，合理指导线路动态增容，保证电网系统的安全稳定运行具有重要意义。

针对架空导线温度场及载流量，国内外已开展了相关研究[4-13]，这些研究分析了风速、风向、环境温度和日照强度等因素对导线工作温度的影响。但是，上述研究主要集中在导线温度场的分析方法方面，对于导线径向温差的分布规律及其对导线允许载流量影响的研究较少。因此，笔者以常用的LGJ300/50钢芯铝绞线为例，采用ANSYS软件建立其精细化有限元模型，综合考虑导线内部空气间隙及线股接触情况，采用数值方法分析架空导线的径向温度场，并与规范IEEE Std 738—2012[14]结果对比，规范最后结合工程实例分析导线允许温度限值的不同定义对其允许载流量的影响，以期望为线路动态增容提供参考。

1 架空导线载流量计算的基本原理

目前，架空导线载流量的计算多采用热平衡理论解析方法[3,12-14]，其基本原理是：当导线热量等于散热量时，达到热稳定，此时导线温度相对恒定。架空导线生热主要包括载流产生的焦耳热和太阳照射热；散热则是导线与外界的对流散热及导线辐射散热。该过程可用稳态热平衡方程(1)表示，从而可得导线载流量，如式(2)所示。

qc+qr=qs+I2RTavg;

(1)

(2)

式中：qc为对流散热量；qr为辐射散热量；qs为日照生热量；I为导线允许载流量；Tavg为导线平均温度；RTavg为平均温度时对应的导线电阻值。

1.1 对流散热量

对流散热量计算如式(3)～(5)，其中式(3)、(4)适于强制对流，式(5)适于自然对流。在低风速时，文献[14]推荐用强制对流和自然对流散热的最大值来表示导线的对流散热量。

qc1=Kangle·[1.01+1.35·Re0.52]·kf·(Ts-Ta);

(3)

qc2=Kangle·0.754 ·Re0.6·kf·(Ts-Ta);

(4)

qcn=3.645 ·ρf0.5·D00.75·(Ts-Ta)1.25,

(5)

式中：Kangle为风向因子，表征风向角对强制对流散热的影响，可由式(6)计算；Re为雷诺数，由式(7)计算；kf为空气导热系数，与环境温度和导线温度等有关系，由式(8)计算；Ts为导线温度；Ta为环境温度；ρf为空气密度；D0为导线直径。

Kangle=1.194 -cosφ+0.194 ·cos 2φ+

0.368 ·sin 2φ,

(6)

式中：φ为风向与导线轴向的夹角。

Re=(D0·ρf·Vw)/μf,

(7)

式中：Vw为风速；μf为空气运动黏度。

kf=2.424 ×10-2+7.477 ·10-5·Tfilm-

(8)

式中：Tfilm为导线与空气接触面的流体定性温度,Tfilm=(Ts+Ta)/2。

1.2 辐射散热量

当架空导线的温度高于环境温度时，导线会对外辐射散热。辐射能力取决于导线与环境的温差。辐射散热量可由式(9)计算，式中包含Stefan-Boltzmann常量σ，其值为5.67×10-8W/(m2·K4)。

qr=17.8·D0·ε·[(0.01Ts+2.73)4-

(0.01Ta+2.73)4],

(9)

式中：ε为导线表面的辐射散热系数[3]，对于光亮新线取0.23～0.43,对发黑旧线或涂黑色防腐剂的导线取0.90～0.95。

1.3 日照生热量

日照生热量与太阳所处位置、太阳常数、线路方位、导线表面的吸热系数等有关，可按下式计算:

qs=α·Qse·sinθ·A′,

(10)

式中：α为导线表面的吸热系数[3]，对于光亮新线取0.35～0.46,对发黑旧线或涂黑色防腐剂的导线取0.90～0.95；Qse为太阳辐射海拔修正值；θ为太阳入射有效角；A′为单位长度导线的投影面积。

1.4 电阻计算

架空导线的电阻因导线的横截面积、频率、电流和温度而异，而且在交流情况下，导线会受到集肤效应、磁滞和涡流损耗的影响，使得导线的电阻增加。笔者按照规范[14]建议值查表选用，表中未列的数值，可用线性插值计算:

(11)

式中：RTl和RTh是当温度分别为Tl和Th时查表所得的导线电阻值。该式可广泛用于计算导线在高温和低温时的电阻，其中包含磁滞效应、集肤效应和绞距系数的影响，但是Th的取值应不小于所要计算的导线温度。

2 导线径向温度场及载流量的模拟

考虑到规范[14]计算导线载流量时无法考虑导线内部温度分布的影响，这与导线实际情况不符。因此，为更准确地指导线路实时增容，保证线路运行安全，有必要准确了解导线内部的温度分布规律。近年来，随着计算技术的发展，采用有限元方法分析导线温度场也趋于成熟[8-10,15]，因此，笔者以下利用ANSYS软件建立导线精细化有限元模型，考虑导线内部空气间隙和线股接触情况，采用数值方法分析其径向温度场。

2.1 计算参数选取

以常用的钢芯铝绞线LGJ120/20、LGJ150/25、LGJ240/40、LGJ300/50、LGJ400/35、LGJ400/65为例进行分析，导线截面特性如表1所示。上述6种导线除截面特性不同外，其他参数均相同：导线的电阻率为2.826 4×10-8Ω·m，电阻温度系数为4.03×10-3K-1，导热系数为237 W/(m·℃)，均为20 ℃时的值[16]。以夏至日、北纬30°、东西走向、平均海拔100 m、环境清洁的导线为例，分析其径向温度分布规律。

2.2 有限元模型的建立

采用ANSYS电热耦合单元Solid69模拟钢芯和铝线，分别赋予其不同的材料属性，其中铝线外表面施加对流换热、太阳辐射热，钢芯和铝线整体施加焦耳热。最终所建的导线横截面有限元模型及网格划分情况如图1所示。

2.3 计算结果分析及对比验证

限于篇幅，以下仅以LGJ300/50导线为例进行分析。取环境温度为20 ℃、风速为0.5 m/s、风向角为90°，当ANSYS模拟的载流量从510 A按步长50 A增加到860 A时，仿真得到的导线径向温度分布如表2所示。为便于比较，表中还给出了对应ANSYS仿真得到的导线不同温度均值时，按照规范[14]中的公式计算的导线载流量。

表1 钢芯铝绞线截面特性

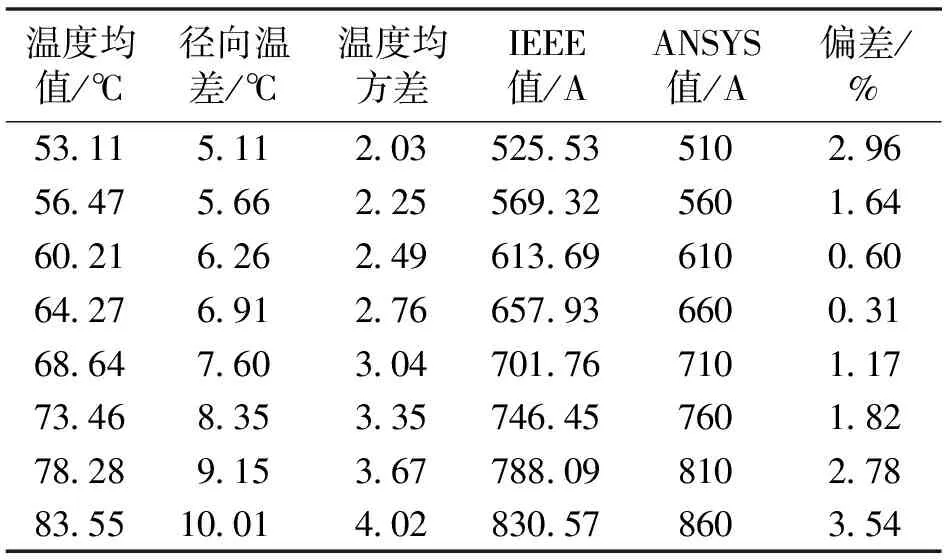
表2 风速0.5 m/s时ANSYS仿真与IEEE理论对比

注：偏差=|ANSYS值-IEEE值|/IEEE值×100%，下同。

考虑环境温度为20 ℃、风速为0 m/s、风向角为90°时，当ANSYS仿真的载流量从410 A增加到760 A时，计算结果如表3所示。

由表2和表3可知：①无论强制对流(风速0.5 m/s)还是自然对流(风速0 m/s)，按照IEEE公式得到的导线载流量与ANSYS仿真值的最大偏差仅为6.21%，说明本文模型是较为可靠的；②随着载流量增加，导线径向温差逐渐增大，可达到4～10 ℃，说明径向温差与载流量存在正相关性。

图2和图3分别给出了风速为0.5 m/s和0 m/s时，载流量为510 A时导线的径向温度。从图2和图3可以看出：导线内部温度呈中心高、表面低的特点，这主要是由导线内部空气间隙及线股间接触情况不同引起的。

为更清楚了解导线径向温度随风速、载流量的变化规律，沿导线径向选取若干测点，提取各测点的温度。当载流量为560 A，风速分别为0、0.5、1 m/s时，导线温度沿径向变化如图4所示；当风速为0.5 m/s，载流量分别为560、610、660 A时，导线温度沿径向变化如图5所示。考虑到导线温度沿径向并非对称分布，笔者分别计算每层导线的平均温度作为该层中心点的温度。当载流量为560 A，风速分别为0、0.5、1 m/s时，导线温度沿径向变化情况如图6所示；当风速为0.5 m/s，载流量分别为560、610、660 A时，导线温度沿径向变化情况如图7所示。

表3 风速0 m/s时ANSYS仿真与IEEE理论对比

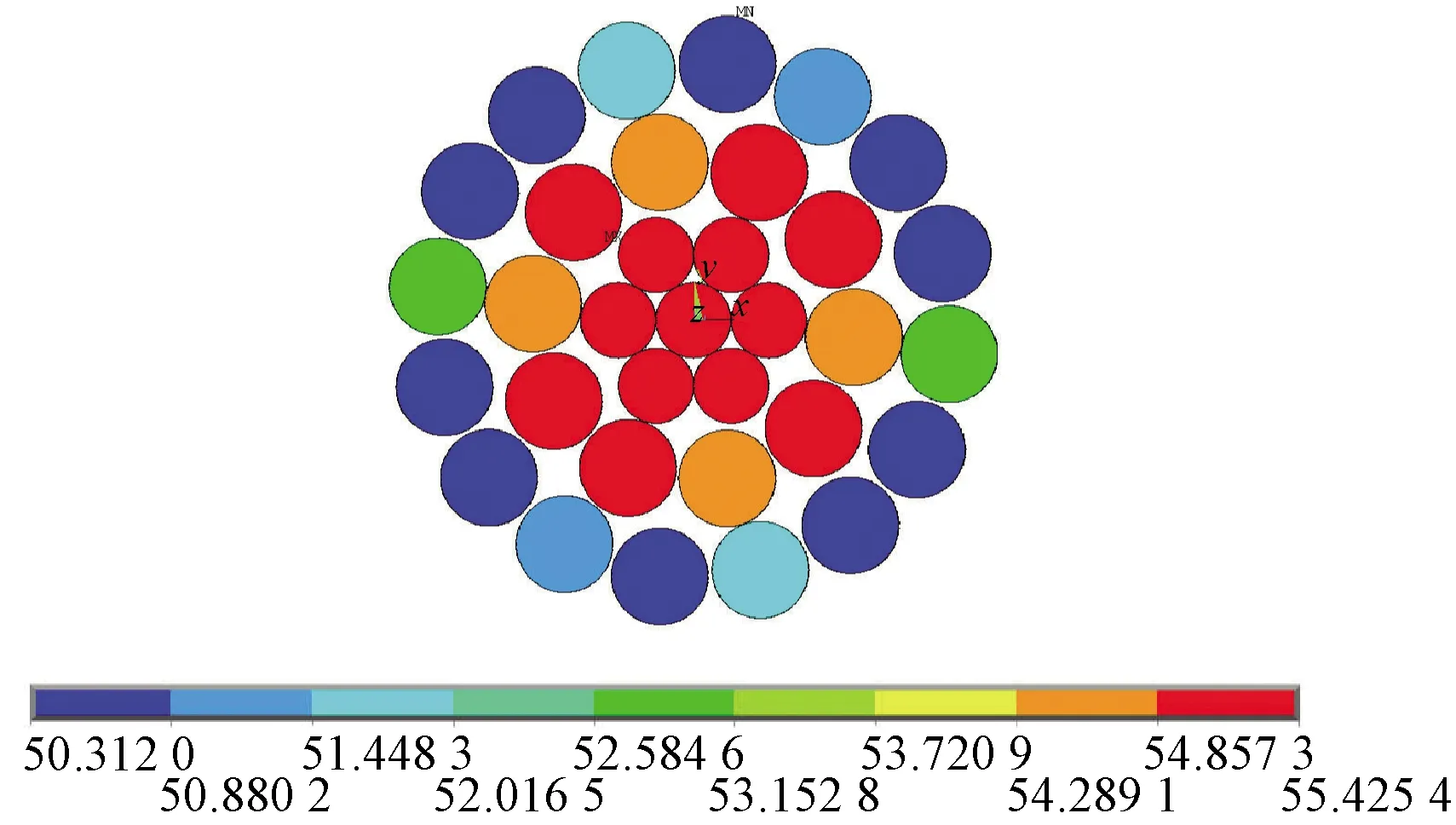
图2 导线截面径向温度分布

图3 导线截面径向温度分布

图4 导线温度沿径向变化(载流量560 A)

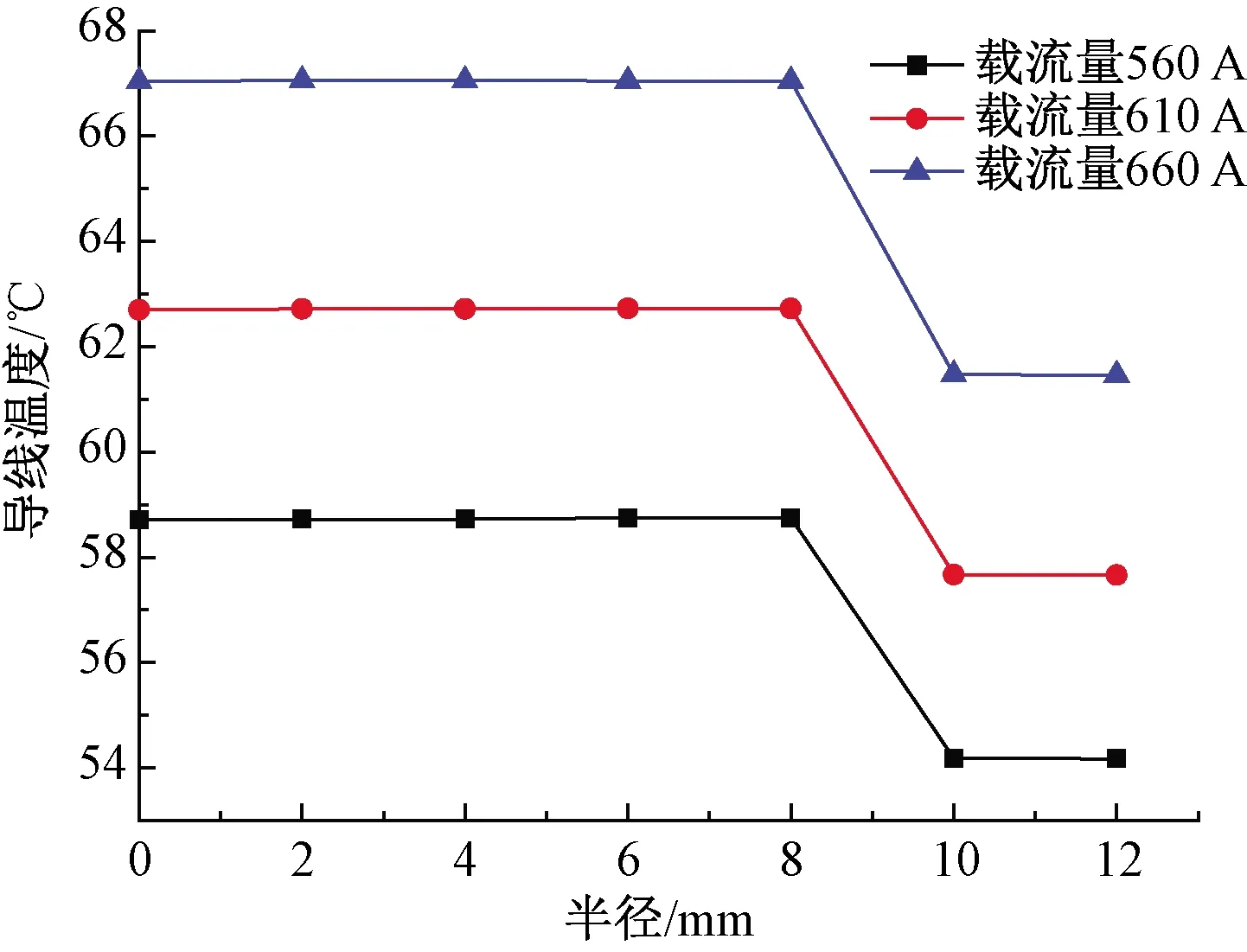
图5 导线温度沿径向变化(风速0.5 m/s)

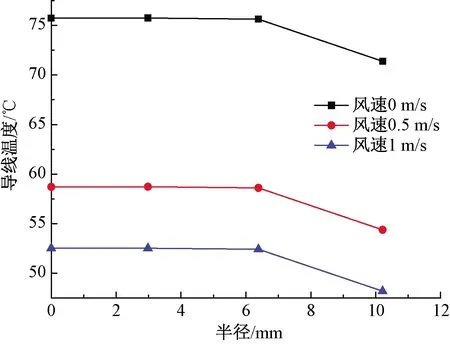
图6 导线各层温度均值沿径向变化(载流量560 A)

图7 导线各层温度均值沿径向变化(风速0.5 m/s)

由图4～图7可知，钢芯和内层铝线温度变化平缓，而外层铝线温度明显降低，这是因为外层铝线与空气直接接触，散热条件有利，而钢芯电阻率较高，载流产生的焦耳热较高，且内层钢芯接触紧密，散热条件差，因此温度较高且变化较小。

2.4 架空导线温度对其影响因素的敏感性分析

选用导线模型内所有节点的平均温度作为导线温度，分析导线温度随风速、风向角、环境温度、日照强度和导线直径等因素变化时的敏感性。为简化，取以下参数进行分析。环境温度20 ℃，风速0.5 m/s，风向角90°，中午12时对应的日照强度，导线型号LGJ300/50，直径为24.26 mm。

导线温度随风速变化特点如图8所示。由图8可以看出，随着风速增加，导线温度逐渐降低。当风速在0～3 m/s时，导线温度对风速变化较为敏感，温度下降较快；当风速大于3 m/s时，温度下降速度趋于平缓。

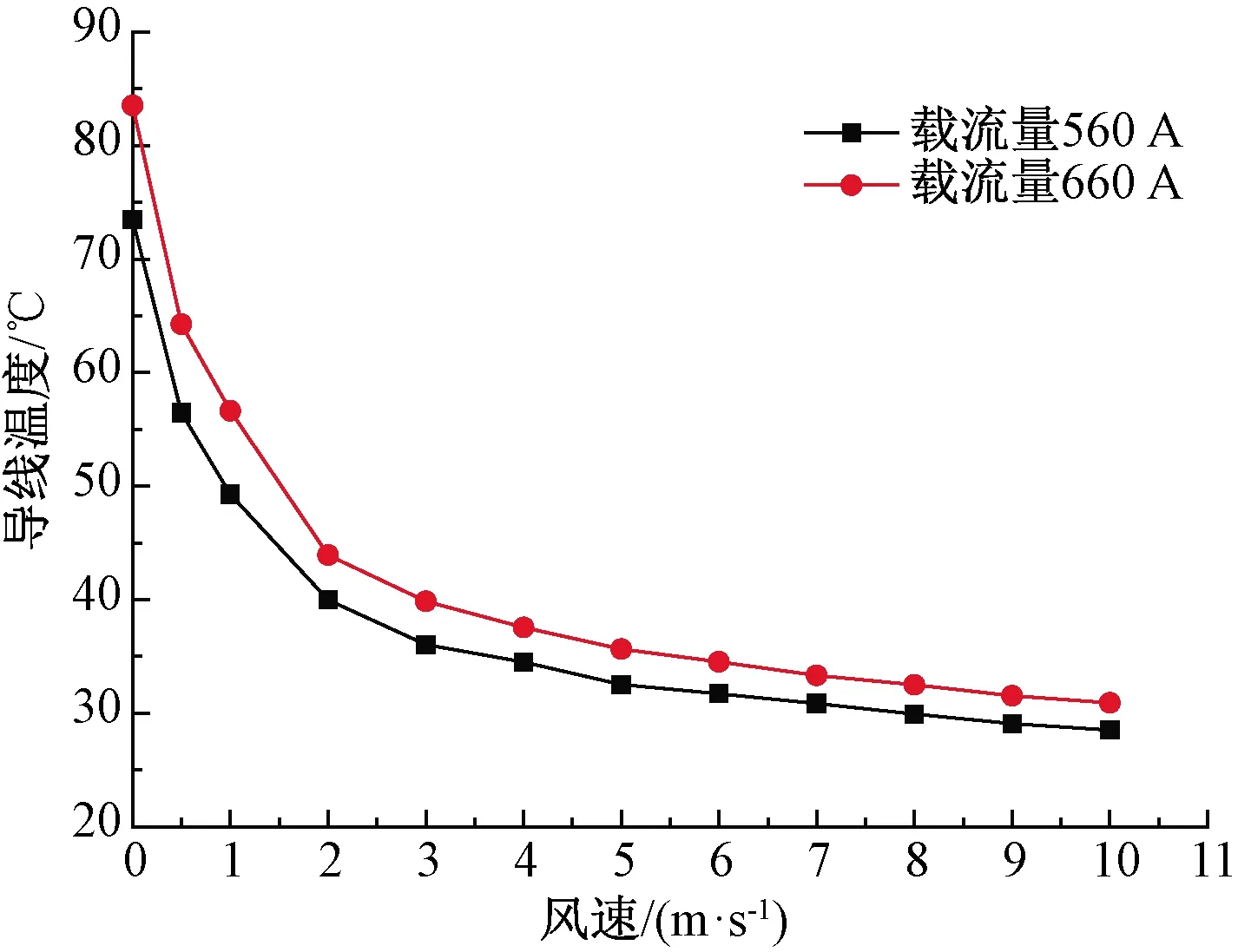
图8 风速对导线温度的影响

风向角变化时，导线温度变化如图9所示。由图9可知，随风向角增大，导线温度降低。当风向角小于45°时，导线温度对风向角变化较为敏感；当风向角大于45°时，导线温度对风向的敏感性降低，温度变化也趋于平缓。

图9 风向角对导线温度的影响

环境温度变化时导线温度变化如图10所示。由图10可知，导线温度与环境温度近似呈线性关系，即环境每升温1 ℃，导线升温约0.9 ℃。这是由于环境温度的升高使空气导热率增加，空气与导线间的热交换加强，因而导线的温升略小于1 ℃。

图10 环境温度对导线温度的影响

日照强度变化时导线温度变化如图11所示。由图11可以看出，导线温度与日照强度近似呈线性关系，日照强度每上升100 W/m2，导线温度约上升1.5 ℃。

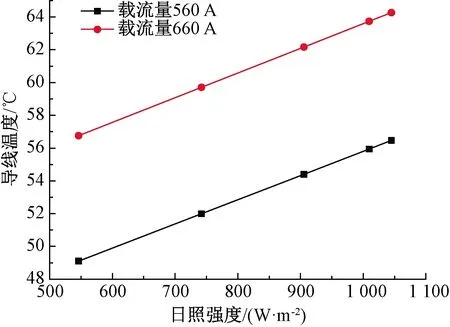
图11 日照强度对导线温度的影响

图12 导线直径对导线温度的影响

当固定载流量，变化导线直径时，导线温度变化如图12所示。图中导线直径分别为15.07、17.10、21.66、24.26、28.00 mm；对应型号分别为LGJ120/20、LGJ150/25、LGJ240/40、LGJ300/50、LGJ400/65。由图12可以看出，固定载流量时，随导线直径增加，导线温度降低，这是因为大直径导线与空气接触面增大，对流散热量增加，因此导线温度降低。

综上可知，导线温度对风速、风向角和导线直径(型号)的变化较为敏感。

3 基于径向温差的导线允许载流量

3.1 径向温差对导线允许载流量的影响

前文分析可知，随载流量变化，导线内部径向温差可达4～10 ℃。为进一步了解径向温差对导线允许载流量的影响，本节仍以钢芯铝绞线LGJ300/50为例，分析径向温差对导线允许载流量的影响，结果如表4所示。

由表4可知，根据导线径向最高和最低温度计算的导线允许载流量差异较大，可达70～80 A，约为导线容许载流量的9 %～13.7 %。这说明，导线径向温差对其允许载流量的影响不可忽视。当考虑径向温差时，由于导线内部温度较高，其实际容许载流量低于以表面温度测算的线路允许载流量。因此，在实际中，如果取导线表面温度的监测结果为导线允许温度限值来调整线路的输送容量是不安全的。

3.2 对规范导线允许温度限值含义及其对导线允许载流量影响的探讨

我国110～750 kV架空输电线路设计规范[3]规定：验算导线允许载流量时，钢芯铝绞线和钢芯铝合金绞线的允许温度宜取70 ℃。该规定虽然给出了导线的允许温度限值，但是并未明确其含义是指导线的表面温度、平均温度还是内部最高温度。当分别按照上述三者理解时，由于径向温差的存在，对应的导线允许载流量也随之不同。为此，本节以江苏电网220 kV旗淮4090线采用的LGJ400/35钢芯铝绞线[16]工程实例进行分析。

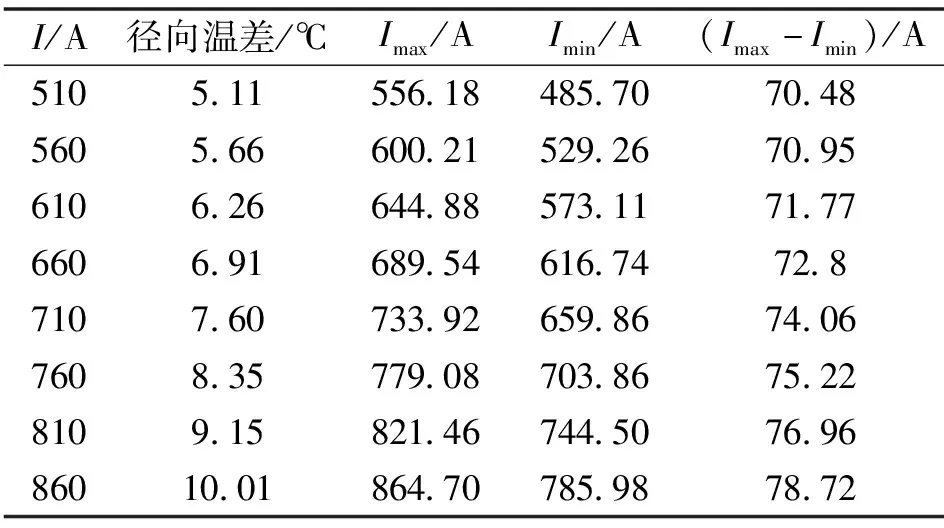
表4 不同径向温差时对应的导线允许载流量

注：I为利用ANSYS仿真导线径向温度场时的载流量;Imax(Imin)为对应ANSYS仿真得到的导线温度最高(低)值时按照IEEE规范公式得到的导线允许载流量。

该导线运行环境温度为40 ℃，风速为0.5 m/s，风向角为90°。按前文方法建立ANSYS仿真模型，如图13所示。

图13 不同允许温度含义对应的导线截面径向温度分布情况及允许载流量

由此可知，当限定导线允许工作温度为70 ℃时，上述3种情况导线允许载流量的差值可达45～124.1 A，约为容许载流量的9.7%～26.9%。这再次说明，线路动态增容时，仅以在线监测的导线表面温度不超过允许温度限值为依据调整线路的输送容量是偏于不安全的。考虑到规范[14]通常按照导线平均温度计算允许载流量，因此，笔者建议可将规范[14]规定的导线允许工作温度限值理解为导线的平均温度。按照笔者分析结果，3种情况导线径向温差在5.55～6.87 ℃，由于实际中更易测得导线表面温度，当控制导线平均温度不超过允许温度70 ℃时，可将测得的导线表面温度控制在60～67 ℃。

4 结论

(1)ANSYS仿真法能较充分地考虑导线内部空气间隙及线股接触情况，较准确地计算导线内部的温度分布情况，可弥补现有输电线路温度监测技术仅监测导线表面温度的不足。

(2)导线运行时，内部径向温差随载流量增加而变化，以LGJ300/50导线为例，径向温差可达4 ～10 ℃，且呈内部温度高、表面温度低的特点。

(3)导线温度的变化在风速0～3 m/s、风向角0～45°时较为敏感；固定载流量时，导线温度随其直径(型号)增加而降低；环境温度、日照强度对导线温度的影响近似呈线性关系。

(4)导线径向温差对其允许载流量的影响不可忽视，温差引起的导线容许载流量变化可超过10%。

(5)考虑导线径向温差时，其允许温度限值的定义对导线允许载流量的影响较大，建议将规范[14]规定的导线允许工作温度限值理解为导线平均温度。