一种基于大气稳定度的风资源评估方法

马晓梅，王 博，刘永前

（1.青海师范大学，青海 西宁 810008；2.新能源电力系统国家重点实验室（华北电力大学），北京 102206）

0 引言

风能资源因其不稳定性和波动性，在建设风力发电场之前，必须对该地区的长期风资源数据进行深入的分析，以全面了解其风能资源，最终实现投资项目的最优控制。在风资源评估的过程中，平均风速、风向、有效小时数等是必须测量的特性参数，这些参数的测量均受地形地貌、大气稳定度、测风时间、测风仪性能和设备安装角度的影响[1]。

大气稳定度表征近地层大气做垂直运动的剧烈程度，表征大气稳定度的参数梯度理查森数（Ri）综合了湍流激发的热力因子和动力因子的作用，反映了更多的湍流状况信息，以此判断大气稳定状态更为准确[2]。

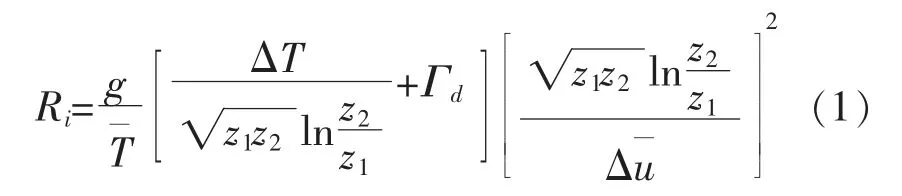
式中：z1，z2为高度；△T，△u 分别为两个高度层的温度差、 风速差；T 为气层平均绝对温度；Γd为干绝热减温率。

当大气层结为中性时，Ri=0；当大气层结为稳定时，Ri＞0；当大气层结为不稳定时，Ri＜0。Ri值越大，大气越稳定。

目前，对大气稳定度在风力发电领域内的研究，一是侧重于对风资源特性的影响研究方面，如不同大气稳定度下的风廓线模型、风切变指数、风速分布等，其主要目的是应用于风资源评估。文献[3]指出，当大气层结为稳定时，风速随着高度的增加而增大的速度比在大气层结为中性时的快。Judit Bartholy[4]认为夜晚的大气较稳定，且夏季的不稳定性明显大于冬季。Nikola Sucevic[5]研究了大气稳定度对风廓线的影响。Sonia Wharton[6]指出，大气稳定度会影响风力发电机组的出力特性。Harvey Seim[7]的研究表明，在稳定大气下，轮毂高度的风速高于中性层结10%以上。文献[8]基于热稳定度风向标准差法的风速外推模型研究表明，考虑热稳定度可以提高风资源评估的准确度。二是气动方面，主要研究大气稳定度对风力发电机组尾流模型和风力发电机组载荷输出功率等的影响。A Sathe[9]提出大气稳定度会影响到塔架和转子的载荷。Matthew J Churchfield[10]的研究表明，不同的大气稳定度等级对风力发电机组的结构响应、发电量和尾流变化模型等都有重要的影响。李广华[11]的研究表明，大气稳定度对海上风电场功率输出影响较大，海陆风对风电场功率输出的影响主要体现在机组尾流间的差异。综上，大气稳定度会影响风资源评估、 风力发电机组选型及风力发电机组设计。但是，以上的一系列研究基本都只关注风资源特性中的一个点，没有考虑大气稳定度修正风资源评估的方法。因此，本文研究了大气稳定度对风资源特性的影响，并建立了考虑大气稳定度的轮毂高度风速外推模型，为科学合理地评估风资源做些基础工作。

1 数据

为了研究大气稳定度对风资源评估参数的影响，本文采用美国科罗拉多州某地的实际测风数据进行分析。本文所采用的测风塔位于美国科罗拉多州的Rocky Flats 湖附近，海拔1 855 m，测风坐标为 35 °51 ′53.34 ″N，105 °14 ′5.28 ″W。测风数据的时间跨度为2007-01-01T0：00-2011-12-31 T24：00，共计 5 a。测风数据包括2，5，10，20，50，80 m高度处的风速、风向、温度等，时间分辨率为1 h。

2 大气稳定度对风资源评估参数的影响

2.1 大气稳定度对风切变指数的影响

风切变指数是一个表征风速随高度、 地表粗糙度、大气稳定度等变化的综合参数。

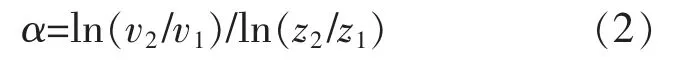
式中：α 为风切变指数；v1为高度 z1处的风速；v2为高度z2处的风速。

在近地面层风廓线中应主要考虑地面粗糙度和低层大气层结情况的影响[12]。即使是同一个地点的风切变指数，在不同时刻会随着大气层结的状态而发生变化。为了研究大气稳定度对风切变指数的影响，根据梯度理查森数的值将每年大气状态分为稳定、中性和不稳定状态，分别计算2007-2010年每年的不同稳定度下的风切变指数（图1），为了减少因为高度差的选择而带来的计算误差，分别计算了利用各高度差得到的风切变指数及其平均值 （平均值用直线表示）。

图1 2007-2010年不同稳定度下风切变指数Fig.1 Wind shear exponent under different atmospheric stabilities（2007-2010）

由图1 可知，风切变指数的变化受大气稳定度的影响，即在不同的大气稳定度下，风切变指数的取值不尽相同。大气由不稳定到中性到稳定，风切变指数的大小逐渐递增，即大气越稳定，风切变指数越大。该地4年内稳定情况下的风切变指数平均值为0.20，中性情况下为0.15，不稳定情况下为0.07，差异明显。稳定情况下的风切变指数是不稳定情况下的3 倍左右。

此外，用来计算风切变指数的高度差对计算结果的影响也很明显。以2007年不稳定情况为例，高度差为2～5 m 的风切变指数为0.045，而利用高度差为10～20 m 计算得到的风切变指数接近0.12，当高度差取10～80 m 时，计算得到的风切变指数在任何一个稳定度下都基本接近年平均值。

综上，计算风切变指数时，考虑大气稳定度的影响，并且选择合理的高度差，对于提高外推计算精度有十分重要的意义。

2.2 大气稳定度对风向及风能玫瑰图的影响

为了研究大气稳定度对风玫瑰图的影响，绘制了2007-2010年不同大气稳定度下的风向玫瑰图和风能玫瑰图（图2，3）。

图2 2007-2010年不同稳定度下的风向玫瑰图Fig.2 Wind rose under different atmospheric stabilities（2007-2010）

图3 2007-2010年不同稳定度下的风能玫瑰图Fig.3 Wind energy rose under different atmospheric stabilities（2007-2010）

每一个风向中不同大气稳定度的比例也展示在图中，而稳定度的比例差异恰好可以解释风向玫瑰图和风能玫瑰图产生差异的原因。以2007年为例，风向玫瑰图中，NW，WNW，S 和 SSE4 个方向的风向分布最多，而S 和SSE 两个方向的风能分布却远小于其他两个方向。究其原因，S 和SSE两个方向虽然风向分布多，但是不稳定大气所占的比例较大。由上面的研究结果可知，不稳定情况下的风速要小，因此，蕴含的风能也就小，最终就造成了风向频率高而风能频率却不同步的结果。

以2008年为例，比较N 和E 两个方向，这两个方向的风向频率接近，但是N 中稳定情况占的频率较大，E 中不稳定情况占的频率较大。在风能玫瑰图中，N 中风能频率明显大于E，即出现频率较高的风向可能因为不稳定情况占的比例大 （风速小），不一定是风能密度较大的方向。

一般情况下，造成风向玫瑰图和风能玫瑰图出现差异的原因是某一风向的平均风速，即该方向不同稳定度所占的比例差异。若某一风向所占的频率大，稳定情况的比例也较大，则该风向所蕴含的风能也大；反之，若某一风向所占的频率大，而不稳定情况的比例较大，则该风向蕴含的风能不一定大。

2.3 大气稳定度对风功率密度的影响

在进行风电场宏观选址时，首先，要求备选地具有的风能质量好，即平均风速高，风功率密度大，利用小时数高。而经过本研究得到，大气稳定度的状态会影响到风功率密度，如果在评估过程中假设大气一直处于中性状态，很有可能错误地估计备选地的风能质量，以至于影响风电场的经济效益。风功率密度为

图4 为各年不同大气稳定度下风功率密度的变化。由图4可知：2007年和 2009年，基本都是稳定情况下的风功率密度最大，中性次之，不稳定情况下的风功率密度最小；2008年只有个别时刻不满足这个规律；2010年，不稳定时风功率密度最小，稳定和中性情况下交替出现，出现这个现象的原因可能是由于2010年稳定和中性情况区分不是很明显，而大气稳定度的分类标准不是绝对的，比如当理查森数属于中性范围，但在很接近稳定标准时，就有可能带来这个结果。总之，大气越稳定，风功率密度越大。因此，在考虑宏观选址时，大气偏稳定的地区风能质量更好。

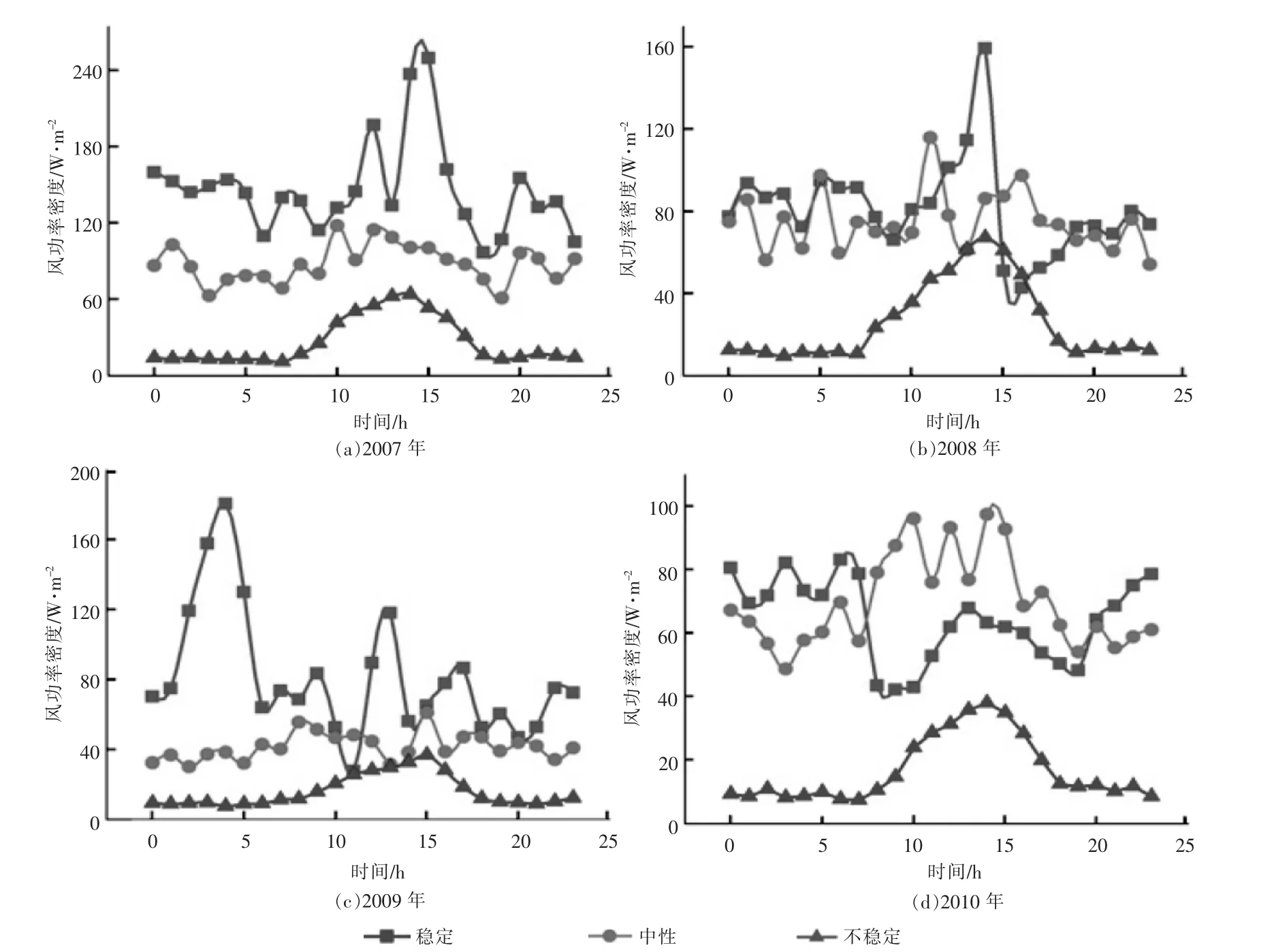
图4 2007-2010年不同稳定度下风功率密度Fig.4 Wind power density under different atmospheric stabilities（2007-2010）

3 考虑大气稳定度的风速外推模型

随着风力发电机组技术的发展，风力发电机组呈现单机容量不断增大，轮毂高度不断增高的趋势，测风塔的测风高度不能满足风力发电机组发展的要求。为了提高轮毂高度风速的外推精度，基于之前的研究，本文建立了考虑大气稳定度的风速外推模型。

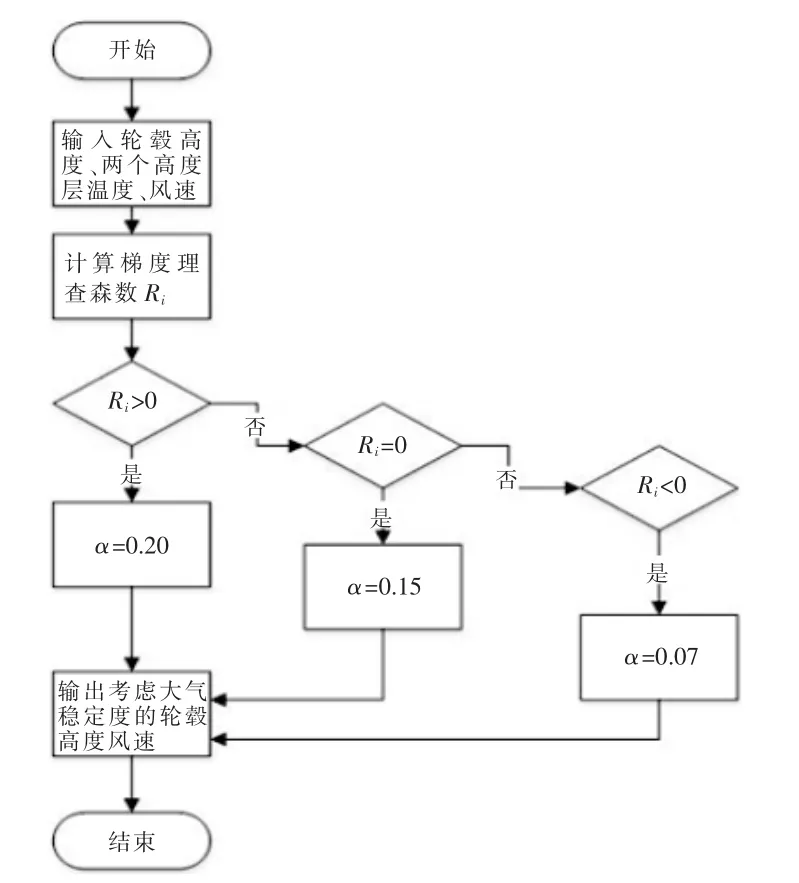
图5 考虑大气稳定度的风速外推模型流程图Fig.5 Wind speed extrapolation model considering atmospheric stability

3.1 模型结构

考虑大气稳定度的轮毂高度风速外推模型结构如图5 所示。

3.2 算例及分析

3.2.1 模型评价指标

在实际应用中，均方根误差对一组测量中的特大或特小误差反映非常敏感，所以，均方根误差能够很好地反映出模型的精密度。因此，本文选择均方根误差来评价模型的精确度。

3.2.2 轮毂高度风速外推结果

分别用两种方法外推轮毂高度的风速，并与实际轮毂高度风速比较，设轮毂高度为80 m。

方法一：不考虑大气稳定度，利用风电场风切变指数的平均值（0.123）直接外推轮毂高度风速；

方法二：用考虑大气稳定度的模型外推。

基于2.1 部分中的讨论结果，当高度差取10～80 m 时，计算得到的风切变指数在任何一个稳定度下都基本接近年平均值，因此，这里用10 m 高度处风速外推80 m 高度（轮毂高度）风速，得到的轮毂高度的平均风速及外推的风速分布参数如表1 所示。

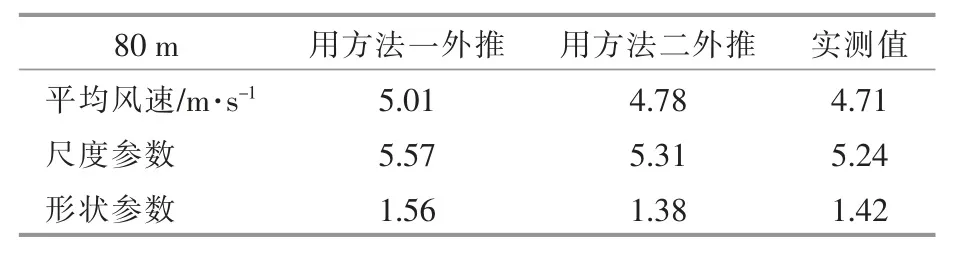
表1 用不同方法外推得到的风资源参数Table 1 Wind resource parameters by different extrapolation methods

由表1 的结果可知，用两种方法得到的轮毂高度平均风速分别为5.01 m/s 和4.78 m/s，而轮毂高度的实测平均风速为4.71 m/s。利用考虑大气稳定度的风速外推模型得到的轮毂高度的风速更接近实测值，这意味着风资源评估、风力发电机组设计与选型及其载荷计算的准确度也将提高。

为了进一步验证模型的实用性及准确性，利用选定的评价指标——均方根误差进行模型准确性的验证。分别计算利用两种方法外推得到的轮毂高度风速的均方根误差，统计得到稳定大气下逐时的均方根误差及不稳定大气下逐时均方根误差。

图6 和图7 分别给出了由不同的外推方法得到的全年风速分布及全年逐时风速均方根误差图。

图6 不同方法外推下的风速分布Fig.6 Wind speed distribution by different extrapolation methods

由图6 可知，本文模型得到的风速分布更符合实际的分布，说明轮毂高度风速的外推结果可行。

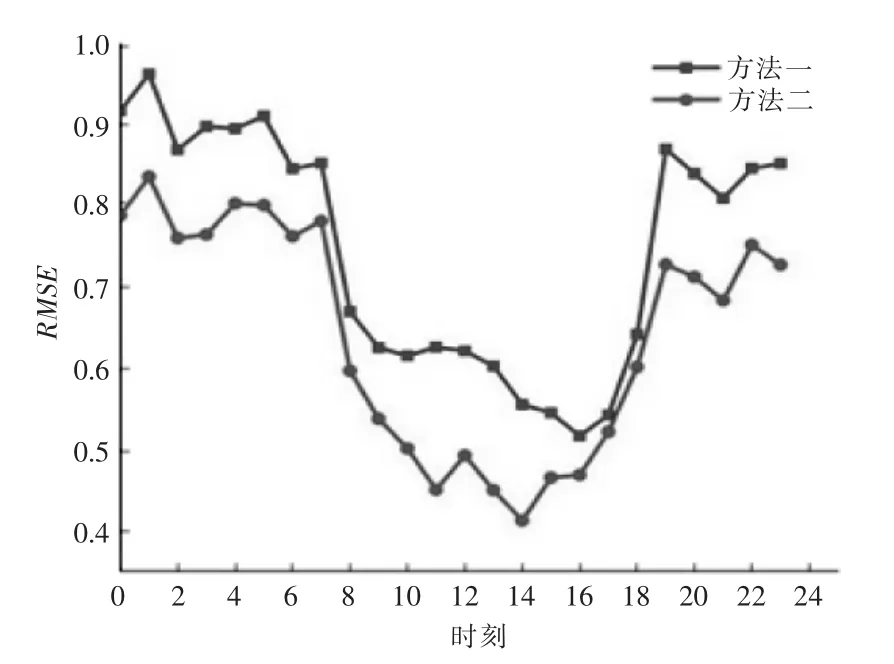
图7 不同方法外推下的逐时轮毂高度风速均方根误差Fig.7 RMSE of wind speed at hub height by different extrapolation methods

由图7 可知，本文模型有效地降低了轮毂高度外推风速的均方根误差，尤其是9-16 时，效果尤为明显，可能是该地不稳定大气占的比例更大，模型在不稳定情况下应用效果更好。

本文模型得到的轮毂高度年平均风速误差减少了0.23 m/s，均方根误差降低了0.12 m/s，因此，本文模型给出的外推方法很好地考虑了大气各因素对风速的影响，得到的结果接近实际值，可以有效提高风资源评估的准确性。

4 结论

风资源评估误差是风电开发项目中的最大风险之一，为有效减小误差，本文研究了大气稳定度对风资源特性的影响，得到以下结论。

①研究了不同大气稳定度下风切变指数、风向玫瑰图、 风能玫瑰图以及风功率密度等的变化趋势，建立了较为系统的大气稳定度和风资源特性参数的对应关系。

②建立了考虑大气稳定度的风速外推模型。算例结果表明： 考虑大气稳定度进行风速外推的方法，外推绝对误差降低了0.23 m/s，均方根误差降低了0.12 m/s；该模型结构简单，工程实用价值高。

③外推模型的输入参量包括轮毂高度外任意两个高度层的温度和风速数据。