注采井间裂缝对地热回灌的影响研究

魏 凯，聂法健，郭 耀，李毅峰，王兴义

（1.长江大学 石油工程学院，湖北 武汉 430100；2.中石油渤海钻探工程有限公司工程技术处，天津 300457；3.青海油田采油五厂，青海 敦煌 736200）

0 引言

地热是一种可再生能源，随着世界各国对能源需求的逐渐增加，地热资源的勘探、开发和利用正逐渐兴起[1]，[2]。目前，受经济、技术等条件的制约，地热主要是通过钻取地下热水的方式将赋存于地热储层中的热能提取出来并加以利用。快速、有效地补充地热储层的水量成为地热资源可持续利用的关键。地热回灌技术是把地热废水、常温地下水和地表水等灌入地热储层内，从而缓解地热储层水量的下降。地热回灌技术已成为实现地热资源可持续利用和地质环境保护的有效手段，并取得了一定的成效[3]。

国内外学者对地热储层及其各项利用技术进行了大量研究。Niyazi Aksoy[4]，Russo S L[5]将理论分析与现场实验相结合，研究了不同地下水抽灌模式对含水层热突破的影响。Freedman V L[6]建立了地下水渗流与热传递耦合模型，分析了地热利用对地热储层热环境的影响。Nam Y[7]通过数值模拟方法，分析了地热储层中的水迁移和热传递过程。曲占庆[8]将地热储层视为由基质岩体与离散裂缝组成的双重介质结构，并基于该双重介质结构建立了温度-渗流-应力全耦合模型。肖鹏[9]建立了三维增强型地热系统水平井平行多裂隙模型，并采用该模型分析了不同注水流量条件下增强型地热系统的运行性能。以上研究为地热资源的有效利用提供了技术支撑，但由于地热储层环境复杂，不同热储地质条件下的回灌效果差异较大，特别是含裂缝的地热储层，其多孔基质与裂缝的双重介质属性会导致地热回灌过程中的渗流和传热现象较为复杂。此外，上述模型均不能科学地表征裂缝对生产井热突破的影响规律。本文考虑渗流对地热储层传热过程的影响，建立了含裂缝地热储层的渗流-传热弱耦合模型，而后结合 “一采一灌”对井注采模式，并利用COMSOL 软件的自定义建模功能对该模型进行求解，最后根据模拟结果分析了裂缝相关特征参数对开采井热突破的影响，为地热储层开发技术的优化奠定了理论基础。

1 含裂缝热储渗流-传热耦合模型

由于含裂缝的地热储层存在多孔基岩和裂缝两种渗流通道，因此该地热储层的热传递过程比单一匀质物体复杂，主要包括以下3 个传热过程：①基岩的热传导；②孔隙流体的热传导和热对流；③裂隙的热传导和热对流。本文忽略回灌水的相变和温度变化对自身粘度以及地热储层渗透性能的影响，建立了含裂缝地热储层渗流-传热耦合模型。

1.1 多孔基岩渗流

假定基岩为匀质的多孔介质，在一定的压力梯度驱动下，回灌水的渗流过程满足Darcy 定律。根据流体的质量守恒定律，可得基岩的稳定渗流控制方程为

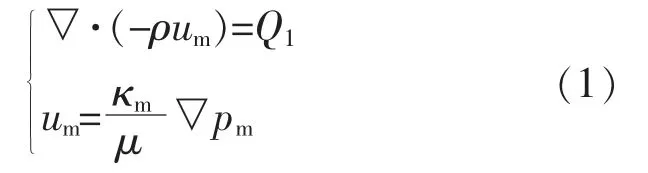
式中：pm为地热储层内部压力，Pa；um为基岩内流体的渗流速度，m/s；κm为基岩渗透率，m2；ρ 为流体密度，kg/m3；μ 为流体的动力粘度，Pa·s；Q1为单位厚度基岩内流体的质量流量，kg/（s·m）。

1.2 裂缝渗流

对于裂缝内的回灌水，采用等效连续模型描述其稳定流动特征。具体的特征方程为

式中：κf为裂缝的等效渗透率；pf为裂隙内部的压力，Pa；Q2为单位高度裂缝内流体的质量流量，kg/（s·m）。

根据立方定律，得到κf的计算式为[10]

式中：df为裂缝的等效直径，m；ff为裂缝的相对粗糙度。

1.3 基岩内的热传递

对于多孔介质，热传递方式主要为岩石颗粒间的热传导、孔隙流体间的热传导和热对流。若基岩为匀质多孔介质，根据能量守恒原理，基岩中的热传递控制方程可表示为

式中：Tm为基岩的温度，K；λe为基岩的等效导热系 数 ，W/（m·K）；λs为基岩骨架的导热系数，W/（m·K）；λl为基岩内流体的导热系数，W/（m·K）；φ 为基岩的孔隙度；ce为基岩的等效比热容，J/（kg·K）；cpl为基岩的流体的定压比热容，J/（kg·K）；cs为岩体骨架的比热容，J/（kg·K）；Qm为基岩的储热量，W/m3。

1.4 裂缝中的热传递

地热储层裂缝内充满回灌水时，热传递方式包括热传导和热对流，具体的控制方程为

式中：Tf为裂缝内流体的温度，K；uf为裂缝内流体的流速，m/s；Qf为裂缝的储热量，W/m3。

1.5 渗流-传热耦合关系

若不考虑流体温度变化对回灌水粘度和储层渗透性的影响，则含裂缝地热储层的渗流-传热过程属于弱耦合过程，即只考虑流体的渗流对多孔介质和裂隙中热传导、热对流的影响，耦合关系如图1 所示。

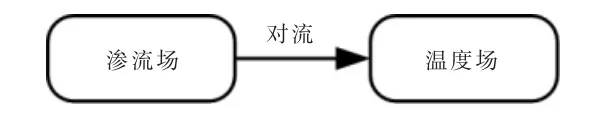
图1 多孔介质和裂隙中渗流与传热的弱耦合关系Fig.1 Weak coupling relationship between seepage field and heat field

根据多孔介质和裂隙中渗流与传热的弱耦合关系，可以将基岩温度场内流体的对流换热速度视为渗流场内流体的流动速度，则um，uf的计算式分别为

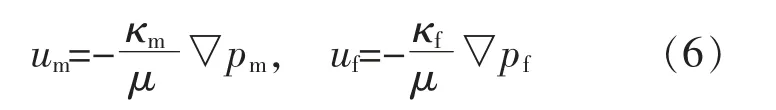
另外，在裂缝与基岩的交界面上，渗流、传热过程均满足连续性条件。该渗流、传热过程的连续性方程分别为

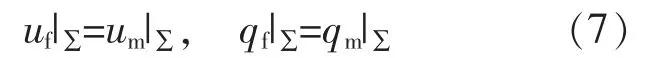
式中：Σ 为裂缝壁面；qf为裂缝内的热通量，W/m2；qm为基岩内的热通量，W/m2。

2 注采井间含裂缝时的回灌开采模型

本文根据建立的含裂缝地热储层渗流-传热数学模型，并结合注采井网方案，建立含裂缝地热储层的回灌开采模型。图2 为注采井间裂缝的二维模型。令回灌温度为Tin；回灌井和开采井之间的距离为L；裂缝位于回灌井和开采井之间，长度为Lf，与两井间的连线夹角均为α。

图2 注采井间裂缝的示意图Fig.2 Schematic diagram of fracture morphology between injection and production well

根据以上物理模型及其假定条件，可以确定相应的定解条件如下。

①初始条件：地热储层的初始孔隙压力为p0，地热储层的初始温度为T0。

②边界条件

渗流场：回灌井、开采井的质量流量均为Qm，地热储层边界处的压力恒为p0。

温度场： 地热储层边界处的温度恒为T0，回灌井注入热量为QT。

QT的计算式为

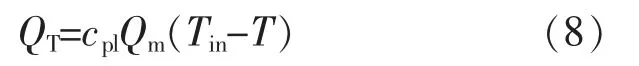
式中：T 为回灌井井底温度，K。

3 裂缝对热突破的影响规律分析

为了分析裂缝对地热回灌热突破的影响，选取雄安新区某地热储层进行实例分析。该地热储层模型的相关参数如表1 所示。

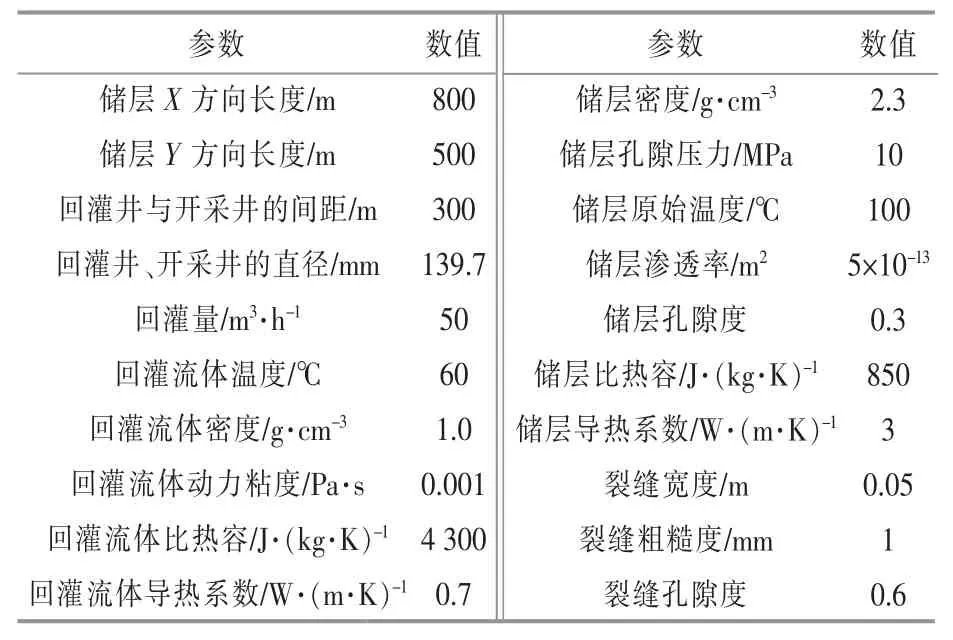
表1 地热储层模型的相关参数Table 1 Main simulation parameters of geothermal reservoir

本文利用COMSOL 软件的自定义建模功能对含裂缝地热储层的渗流-传热弱耦合模型进行求解。其中，裂缝采用线单元进行剖分、热储层采用三角单元进行剖分。为了提高计算精度，对回灌井、开采井和裂缝等区域进行了局部网格细化。含裂缝地热储层的二维有限元模型见图3。

为了消除网格划分和时间步长对模拟结果的影响，并着重分析生产井的热突破现象，本文以生产井温度为监测变量，对含裂缝地热储层的二维有限元模型进行网格独立性和时间独立性检验。检验结果如图4 所示。图中：n 为裂缝处的线单元数；N 为储层面单元的个数；t 为时间步长。

图3 含裂缝地热储层二维有限元模型Fig.3 2D FEM of fractured thermal reservoir

图4 独立性检验结果Fig.4 Verification of grid independence and time independence

由图4（a）可知，当 n 为 40、N 为 4 706 时，网格划分对生产井热突破的影响较小。由图4（b）可知，当t 为0.1 a 时，该参数对生产井温度没有影响。若时间步长取得太小，将增加计算工作量，若时间步长取得太大，则会影响计算精度。综合考虑得到，应取 n≥40，N≥4 706，t≤0.1 a。

图5 为无裂缝以及不同裂缝倾角条件下，地热储层渗流场、温度场的分布情况。图中：云图为温度分布图，箭头为渗流速度分布图。

由图5 可知，裂缝对地热储层的温度场、渗流场，以及开采井的热突破现象均有较大影响，渗流场的变化加剧了热对流过程的进行。

当裂缝长度为200 m、宽度为40 mm 时，无裂缝以及不同的裂缝倾角θ 条件下，开采井温度随时间的变化情况如图6 所示。

图5 无裂缝以及不同裂缝倾角条件下，地热储层渗流场、温度场的分布情况Fig.5 Distribution of seepage field and temperature field in geothermal reservoir without fracture and with different crack dip angles

图6 无裂缝以及不同的裂缝倾角条件下，开采井温度随时间的变化情况Fig.6 The change of temperature of production well with time under the condition of different fracture obliquity and no fracture

由图6 可知，在无裂缝以及裂缝倾角分别为0，30，45，60，90 °的条件下，开采井的热突破时间分别为 5，11，20，29，32，35 a。通过对比可以看出，裂缝倾角越小，开采井的热突破时间越短，当裂缝处于回灌井与开采井之间的连线上时，开采井的热突破时间越短。因此，对注采井网进行设计时，应尽量使裂缝与注采井之间的夹角最大化，从而延缓开采井热突破发生的速率。

当裂缝倾角为0°、宽度为40 mm 时，不同裂缝长度L 条件下，开采井温度随时间的变化情况如图7 所示。由图7 可知，当裂缝长度分别为50，100，150 m 时，开采井的热突破时间分别为33，24，17 a，由此可知，裂缝长度越长，开采井越容易发生热突破。

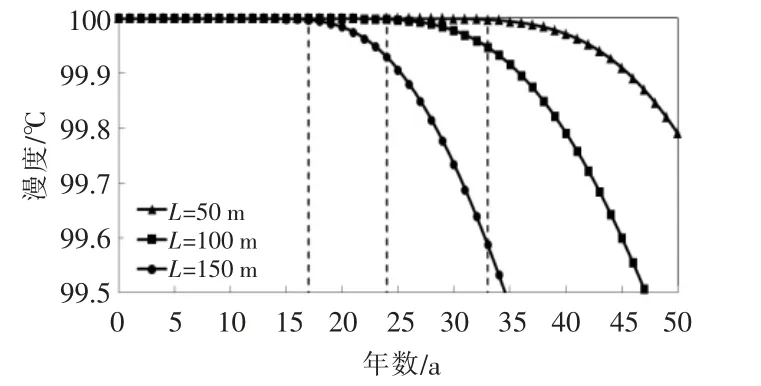
图7 在不同的裂缝长度情况下，开采井温度随时间的变化情况Fig.7 The change of temperature of production well with time under different fracture length

当裂缝长度为200 m、倾角为0 °时，不同裂缝宽度d 条件下，开采井温度随时间的变化情况如图8 所示。

图8 在不同的裂缝宽度情况下，开采井温度随时间的变化情况Fig.8 The change of temperature of production well with time under different fracture width

由图8可知，当裂缝宽度分别为 20，60，100 mm 时，开采井热突破时间分别为 22，14，12 a，由此可知，裂缝越宽，开采井越容易发生热突破。

4 结论

本文考虑渗流对地热储层传热过程的影响，以多孔介质传热理论为基础，建立了含裂缝地热储层的渗流-传热弱耦合模型，并结合 “一采一灌”的对井注采模式，分析了裂缝倾角、长度、宽度对地热储层渗流场、温度场的影响规律。分析结果表明：①裂缝倾角、长度、宽度对地热储层热突破现象影响较大，裂缝的倾角越小、长度越大、宽度越宽，生产井越容易产生热突破，并且当裂缝处于注采井连线上时，热突破发生的速率较快；②在裂缝的相关特征参数一定时，通过优化注采井与裂缝之间的方位关系，可以延缓生产井热突破发生的速率。