科学“睡美人”现象研究

李品保 王幼军

摘要：以CNKI数据库1892—2009年数学史主题1952篇论文为研究对象，采用严格的“睡美人”指标对其进行检索，对识别出的“睡美人”论文的基本概况、存在原因进行具体分析，并进一步对“睡美人”现象在不同领域论文中的存在原因、表现程度作差异分析。研究发现，“睡美人”现象在数学史主题论文中表现可能更为明显；即使是权威发表论文也可能被忽视。

关键词：“睡美人”；延迟承认；数学史；数学教育

中图分类号：G301文献标识码： ADOI：10.3969/j.issn.1003-8256.2020.04.012

开放科学（资源服务）标识码（OSID）：

1问题的提出

科学界存在认识延迟的现象：科学成果发表初期几乎无人关注，过了一段时间后又突然吸引大量关注并为科学界所承认，这种现象被称为“阻滞发现”“延迟承认”等。在学术论文中表现为一篇论文发表后多年内几乎无人或很少人关注，获得零被引或低被引；在一段时间后又突然受到大量关注，获得较高被引或高被引，而这种论文又对该领域研究有较重要的影响，这种遭遇“延迟承认”的论文被称为“睡美人”论文。“睡美人”论文最早由荷兰莱顿大学科学技术研究中心（CWTS）的Anthony F. J. van Raan[1]于2004年的一篇名为“科学中的睡美人”中提出。他称那些发表后相当长的一段时间内几乎不被任何人关注，就像格林童话中的“睡美人”一样在沉睡，在某个时刻又突然吸引很多人注意的论文为“睡美人”论文，唤醒“睡美人”论文的论文则被称为“王子”论文（Prince Literature）。“睡美人”论文动态地反映了引文的时间特征和历史过程，是从文献计量学的角度定量地描述了科学领域中的“延迟承认”现象。

早期学者多是从科学史的角度对“睡美人”进行不系统的研究，随着研究方法的系统化，人们重新发现并肯定了物理、化学等领域“睡美人”论文的价值，关于“睡美人”的研究也逐渐升温。迄今最大规模的“睡美人”论文研究对1900年以来Web of Science收錄的发表在自然科学及社会科学领域2000多万份被引次数至少为1次的论文进行系统分析后发现，物理学、化学和数学中的“睡美人”论文最多[2]；S. Redner[3]研究了Physical Review期刊上近110年具有“睡美人”特征的文献；梁立明等[4]曾对一篇被迟滞承认的超弦理论论文进行研究；杜建等[5]利用被引速率指标研究了2014年诺贝尔化学奖得主Stefan Hell的“睡美人”文献。姚建文等[6]研究了我国CSSCI中图书情报学领域中的“睡美人”文献；袁红等[7]研究了国内图书情报学、物理学及医学三大学科领域“睡美人”文献，等等。国际上关于“睡美人”文献的研究成果比较丰富，在研究方法、研究对象的选择上已经十分成熟；国内“睡美人”研究在学者们的共同努力之下也渐趋成熟，尤其擅长追踪“热点”研究或对“热点研究”进行研究，但距系统研究国内所有科学领域中可能存在的“睡美人”文献的目标仍有较大距离。

本文将通过“睡美人”视角去审视及评析国内数学史主题论文中可能存在的曾被忽视但对该领域影响较大的研究成果，试图回答以下问题：相比物理学、医学等热门研究领域，以数学史为主题的“冷门”研究中是否也存在“睡美人”？存在原因具体是什么？因其“冷门”属性，“睡美人”论文在这一主题领域和其他领域中的存在原因、具体表现是否一致？

2研究设计

2.1已有研究方法

学界目前广泛采用的有两种研究方法，第一种是van Raan在“科学中的睡美人”一文中给出的界定“睡美人”论文的三项指标：沉睡时长（length of the sleep），即论文处于零被引或低被引状态的时间，他在文中考察了沉睡时长为5到10年的案例；沉睡深度（depth of sleep），即按照论文在考察的沉睡时长内，年均被引1次及以下称为深度沉睡（deep sleep），年均被引1到2次称为沉睡（less deep sleep）；唤醒强度（awake intensity），即论文在紧接睡眠期之后的4年内被引用次数（不包括自引），这4年被称为唤醒时期（awaking period）。唤醒强度还可以分为5个等级：（21，30），（31，40），（41，50），（51，60），（60<）。van Raan曾按照一个比较严格的阈值，即论文发表后10年内年均被引次数不超过1次，被唤醒后10年内年均被引次数要大于5次，来识别物理学、化学、工程学与计算机科学领域的“睡美人”论文[8]。

其中Cn是论文在考察期内的总被引次数，Ci是第i年的被引次数，n是论文的年龄。被引速率的值越小，则其前后时段被引频次的差异性越大，说明论文的“睡美人”特征越明显。有学者在此基础上以被引速率0.4、0.5和0.6为分界点，将论文分为：延迟承认型（CS<0.4）；昙花一现型（CS>0.6）；厚积薄发型（0.4

2.2研究方法

van Raan[1]的三项指标属于主观指标，Wang J[9]提出的被引速率属于客观指标，均存在一定局限性[11]。本文引入van Raan界定“睡美人”论文的三项指标，结合论文发表后需经10年被引、沉睡时长需大于等于5年、被引速率阈值设定为0.4、总被引次数排该主题文献前1%为高被引文献等指标，最终确定本文所研究的“睡美人”论文必须同时满足6个指标：

a.属于高被引文献；

b.被引速率小于0.4；

c.年龄大于等于10年；

d.沉睡时长大于等于5年；

e.睡眠期内年均被引次数小于等于2；

f.被唤醒后4年内总被引次数大于等于21。

以CNKI中国学术期刊网络出版总库为数据源，采取综合识别指标检索自1892年至2009年“数学史”主题共1952篇论文，识别出唯一一篇同时满足以上6个条件，具有“睡美人”特征的论文。该文于1994年发表于《数学教育学报》，题目为《数学哲学、数学史与数学教育的结合—数学教育改革的一个重要方向》[12]（以下简称《数学教育改革》），作者为徐利治先生、王前先生。

3结果分析

3.1基本概况

从表1看出：截至2019年10月，该文在CNKI数据库数学史主题共4455篇论文中总被引次数排名第6，总被引次数排该主题论文约前0.13%，高于目前多采用的排前1%为高被引论文的标准，属于高被引论文。

本文所检出“睡美人”论文《数学教育改革》的详细信息整理见表2。从表2可知，此文的沉睡强度可以分为两个时间段：1994—1998年，该论文年均被引次数（不含二级引证文献数量）为0.8，沉睡强度为深度沉睡；1994—2005年，该论文年均被引次数约为1.6，沉睡强度为沉睡。该文的唤醒强度位于（21，30）区间，属于最低等级。

3.2存在原因分析

此文在发表后12年内一直处于沉睡期，但从之后的引用表现来看此文在该领域的研究又扮演着重要角色。那么，该论文之所以遭遇延迟承认成为“睡美人”的原因是什么？可以从两个方面具体分析。

3.2.1未获得及时关注的原因

第一，该文研究内容涉及多学科，不能及时获得广泛承认。以“数学史”为主题的研究总共可为两大类：一是着重于数学史本身，分析国内外数学史研究现状或趋势等，如表1中排名14的《中国数学史研究范式的转换》；二是将数学史与数学教育相结合，着重于讨论数学史对数学教育产生的影响等等，如本文所讨论的《数学教育改革》。

1972年第二届国际数学教育大会上，数学史与数学教学关系国际研究小组（HPM）成立，标志着数学史与数学教育的关系正式成为一个学术研究领域[13]。《数学教育改革》则是在国内外数學教育界对数学史和数学哲学的兴趣逐渐升温的背景下诞生的。作者认为需要从理论上和实践上对这种趋势进行分析研究，从而使这种教育改革得以深入、持久地展开下去。作者提议在数学教育中引进新的教学手段和方法，把数学史和数学哲学的研究成果运用于数学教育过程之中，力促数学的哲学、历史和教育三者的有机结合，将研究视野扩展到了多个学科。该论文属于国内相关研究领域较早的一批研究之一。此外，作者还从数学本体论、认识论和方法论三个方面谈论将数学哲学研究成果运用于数学教育中，认为对培养学生的数学思维能力有重要帮助；重视数学史对教育的作用，尤其是“外史”方面，而“外史”研究的内容涉及教育、哲学、宗教和社会等方面，需要从多学科的视域来考察数学与社会生活各方面的关系。

该文于1994年发表后引起了国内极少数学者的注意，但数学史及数学哲学等对数学教学的意义并没有得到及时的广泛承认，这意味着要求该领域的研究学者必须同时具备一定的数学、教育学、历史学和哲学等知识，这在增大相关学者研究难度的同时，也提高了相关学界的评价难度，最终无法获得学术界的广泛理解。

第二，发表越早，面临传统阻碍越多。《数学教育改革》一文是自1892年始CNKI中国学术期刊网络出版总库数学教育主题论文中最早在题目和内容上明确提出要将数学史、数学哲学与数学教育结合起来的论文。此外，该文发表于20世纪90年代，而学界当时仍在对自20世纪60年代以来关于“新数学”教育是非功过进行争论。该文借鉴国外先进教育经验，重新审视了这场争论，认为这些争论也是在数学史和数学哲学的背景下进行的。

一方面该文早于1994年就已发表，从这点来看，该文可以抢得先机，更早获得学界关注，被引时间也更长；但从另一方面来看，越早发表就意味着可能面临越多传统的阻碍，不能获得学界及时认可的可能性也就越大。

3.2.2得到重视的原因

第一，研究热点的兴起。自从2005年第一届全国数学史与数学教育研讨会召开以后，数学史在数学教育中的作用日益受到关注[14]。从表2可知，该文于1994年发表后5年内处于深度沉睡，12年内处于沉睡，并未及时获得当时科学界的较多关注。从图1可见，该文2005年被引5次，2006、2007年更是都达到9次被引。正是由于国内自2005年起数学史在数学教育中的作用研究成为热点，该文才突然得到大量关注，从而于当年被唤醒得以成为真正的“睡美人”论文。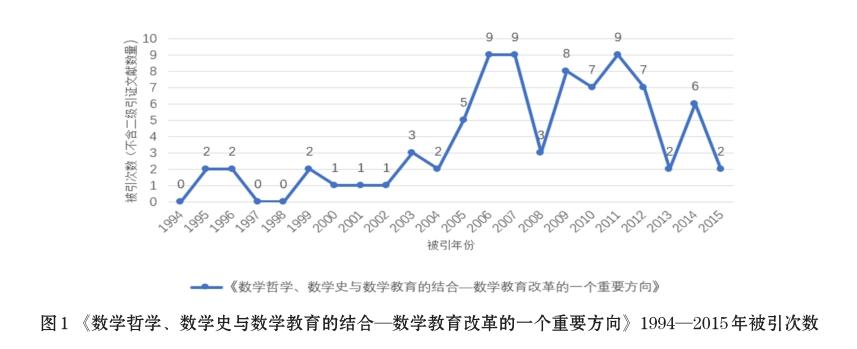

第二，基于发表期刊的权威性。《数学教育学报》创刊于1992年，由中国教育学会和天津师范大学主办，是目前国内数学教育领域最高层次的学术期刊。另外，从表1可知，CNKI数据库中数学史主题被引次数前20名论文中，有10篇发表在《数学教育学报》上，可见该研究领域的学者对该期刊的认可度之高，该刊发表的论文在该研究领域的影响之大。这也是该文之所以能在几年甚至几十年后仍受到较多关注，从较低被引到高被引的重要原因之一。

第三，论文质量过硬。首先，上文提到的该文未获得及时关注但如今却成为高被引论文说明该文具有前瞻性等重要价值；其次，提出的建议可操作性强。该文结合现实热点问题和教育需求，在讨论将数学哲学、数学史融入数学教育的重要意义和将三者结合起来实施的困难后，还提出了五项颇具建设性的具体措施，比如在高等教育中增加了数学哲学和数学史方面的内容以培养师资；新编含数学哲学和数学史相关成果的数学教材；开展三者结合的学术活动等等，这些措施如今均已得到有效实施并取得良好效果；最后，影响深远。该文作为被引速率低的高被引论文说明了该文的学术生命力强，而论文的学术生命力越强，对该研究领域的学术贡献可能越大，该文至今在同研究领域文献中仍受到持续关注和引用。当然，论文质量过硬正是“美”之所在。

3.3差异分析

将“睡美人”现象在数学史主题领域和其他领域中的存在原因、表现程度作以下差异分析：

3.3.1存在原因差异分析

权威发表论文同样面临被忽视的可能。有学者研究发现，van Raan识别出的“睡美人”论文的作者L.J. Romans发表论文时刚博士毕业不久，为该领域的一名新秀，因此认为人们只会更多关注权威们的工作而不会引用新秀的论文。本文所识别出的“睡美人”论文《数学教育改革》的第一作者为徐利治先生，徐先生是中国著名数学家、数学教育家和数学哲学家，其在数学研究、数学哲学和数学教育方面均做出了创造性的贡献[15]。在该文发表前，徐先生曾担任大连理工大学应用数学研究所所长、中国组合数学研究会第一任理事长等职，已发表多篇关于数学研究、数学教育等方面的重要论文。即使像徐先生这样的权威发表论文同样可能被忽视，这说明“睡美人”论文之所以“沉睡”的主要原因可能并不在于作者本身，即并非“名声不够”，而可能在于论文的内容涉及面、发表时间等，即所谓“生不逢时”。

3.3.2表现程度差异分析

有学者曾对“睡美人”现象在图书情报、医学和物理学领域中的表现作对比研究，研究发现“睡美人”现象在这三个领域中表现明显程度依次降低。而一般认为图书情报领域相比医学、物理学领域来说更为“冷门”，由此可推测，“睡美人”现象在相对“冷门”领域中表现可能更为明显。经本文案例研究，可得以下两点具体差异表现：

存在概率正常偏大。从截至目前有关“睡美人”论文大规模的分析来看，在严格的指标界定下“睡美人”论文的正常比例约为万分之一到千分之一[8]，总体来说是较罕见现象。本文以严格的指标（6个条件）对数学史主题论文进行筛选，在1952篇论文中发现1篇“睡美人”论文，“睡美人”现象存在概率为1/1952，属于正常范围，但不可否认的是“睡美人”现象在国内数学史主题论文中存在的概率在正常范围内偏大。

沉睡时长可能更长。该研究还发现在这三大领域中“睡美人”论文在沉睡期间的平均沉睡时长依次递减，分别为10、8.45、7.78。本文在数学史主题论文中只发现一篇符合本文严格条件的论文，平均沉睡时长为12，可以看出“睡美人”论文在国内数学史主题这类“冷门”领域中沉睡时长可能更长。

经分析，可以认为“睡美人”现象在数学史主题论文中表现可能更为明显。

4结语

首先，“睡美人”在数学史主题论文中存在。

其次，与其他热门领域如物理学、医学等相比，“睡美人”现象在数学史主题一类的“冷门”研究领域中的表现更为明显，具体表现为存在的概率正常偏大、沉睡时长可能更长。

再次，“睡美人”现象在数学史主题论文中存在的原因可以从“未获得及时关注”和“得到重视”两个方面来具体分析。存在原因与之前研究所得原因也并非完全一致，从本文研究来看，主要原因并非作者“名声不大”等，即使是权威发表论文同样面临被忽视的可能，而是因为论文“生不逢时”。

最后，本文采取严格条件进行筛查的目的是为了分析国内数学史论文中可能存在的“睡美人”特征最为明显的文献，但是，这样也不可避免地忽视了较高被引中可能存在的具有重大意义的论文。此外，在国内其他数据源中数学史主题研究领域的“睡美人”论文存在情况如何？书籍中是否也存在“睡美人”？这都有待更多的实证分析。

参考文献：

[1]VANRAAN A FJ.SleepingBeautiesinscience[J]. Scientometrics， 2004， 59（3）： 467-472.

[2]WANG J， MA F， CHEN M， et al. Why and how can" sleeping beauties" be awakened？[J]. The Electronic Library， 2012， 30（1）： 5-18.

[3]REDNER S. Citations statistics from 110 years of physical review[J]. Physics Today， 2005， 58（6）： 49-54.

[4]梁立明，林曉锦，钟镇，等.迟滞承认：科学中的睡美人现象：以一篇被迟滞承认的超弦理论论文为例[J].自然辩证法通讯， 2009， 31（1）： 39-45.

[5]杜建，武夷山.基于被引速率指标识别睡美人文献及其"王子"——以2014年诺贝尔化学奖得主Stefan Hell的睡美人文献为例[J].情报学报， 2015， 34（5）： 508-521.

[6]姚建文，赵庆华，吴丽萍.图书情报论文的睡美人现象考察[J].大学图书馆学报， 2014， 32（3）： 64-68.

[7]袁红，杭培培.不同学科领域"睡美人"论文的比较分析[J].情报资料工作， 2016， 37（2） ： 34-38.

[8]杜建，武夷山. "睡美人"论文的重要特征、预测线索与政策启示[J].科学学研究， 2018， 36（11）： 1938-1945.

[9]WANG J. Citation time window choice for research impact evaluation [J]. Scientometrics， 2013， 94（3）： 851-872.

[10]杜建，武夷山.睡美人与王子文献的识别方法研究[J].图书情报工作， 2015， 59（19）： 84-92.

[11]开滨，姚艳玲.自然科学领域中睡美人文献跨学科特征实证研究——以SCI中6大学科为例[J].情报杂志， 2018， 37（8）：145-152.

[12]徐利治，王前.数学哲学、数学史与数学教育的结合——数学教育改革的一个重要方向[J].数学教育学报， 1994， 3（1）： 3-8.

[13]汪曉勤，欧阳跃. HPM的历史渊源[J].数学教育学报， 2003， 12（3）： 24-27.

[14]沈中宇，邹佳晨，汪晓勤. ICME-13之HPM专题研究综述[J].数学教育学报， 2017， 26 （5） ： 71-76.

[15]沈威.徐利治数学教育思想研究[J].数学教育学报， 2019， 28（1）： 74-78.

Study on the Phenomenon of "Sleeping Beauty"： Centered with the Thesis in the Subject of History of Mathematics

LI Pinbao，WANG Youjun（ College of Philosophy， Law & Political Science，Shanghai Normal University， Shanghai 200234，China）

Abstract： Based on CNKI database， 1952 papers in the subject of history of mathematics from 1892 to 2009 were searched by using strict identification index of "sleeping beauty". To analyzes the basic situation， existing reasons of the identified"sleeping beauty" papers， and further analyzes the existing reasons and performance degree of "sleeping beauty" phenomenon in different fields. It is found that the phenomenon of "sleeping beauty" may be more obvious in the subject of history of mathematics， and even the authoritative papers may be ignored.

Keywords： "sleeping beauty"；delayed recognition；history of mathematics；mathematics education