二维周期阻尼薄板声辐特性探究

郭亚敏，郭冬青

（1.山西省工业管理学校， 山西 太原030012； 2.河南工程学院， 河南 郑州451191）

研究发现， 弹性波在具有周期结构的材料 （如声子晶体） 中传播时， 在某些频段内存在通带和禁带特性[1-2]， 基于这种特性， 产生了许多相关的研究成果； 温激鸿等人[3]研究了材料的密度和刚度以及几何参数对一维二维三维声子带隙特性的影响， 并定性总结出相关的结论。 何力功[4]根据不同的声子晶体结构， 研究了它们起始频率和截止频率的分布特点， 以及声子晶体隔声带隙的影响因素。 周明钢等[5]针对车辆驾驶室存在的低频噪声问题， 根据研究的低频带隙相关结论对驾驶室进行了改进。

本文基于二维周期阻尼薄板结构探索性地研究了二维周期阻尼薄板结构的振动与声辐射特性， 探讨了相应结论， 以期不断丰富周期阻尼的结构形式， 为实际应用提供理论方法指导。

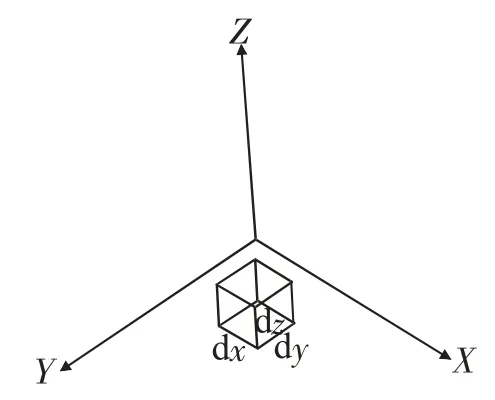
图1 薄板和阻尼块结构模型

1 隔声特性和隔声辐射的理论计算

1.1 隔声特性理论

根据薄板变形理论， 假设薄板和阻尼块的弯曲变形是相同的， 其结构模型见图1， 沿X 轴和Y 轴方向的周期性阻尼结构分别施加到基板上。

在简谐力作用下， 二维周期阻尼薄板结构的振动方程为

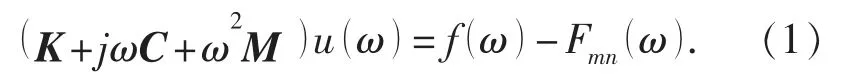
式中： K 为结构的刚度矩阵； C 为结构的阻尼矩阵；M 为结构的质量矩阵； f(ω )为外部激励载荷； Fmn(ω )为阻尼阵列的第m 行、 n 列的周期阻尼块与基板之间的相互作用力。 其中Fmn(ω )的解析式未知，由于周期阻尼的多样性， 使得其解析式难以统一，因此要得到解析式宜采用有限元思想进行周期阻尼结构的离散， 获得的离散节点振动方程[6]为

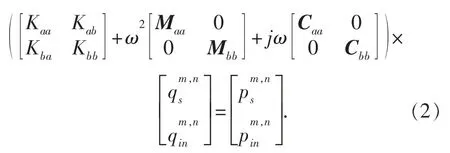
在总体刚度矩阵中， 周期阻尼内部节点作用力相互抵消， 因此对式 （2） 进行变换得到

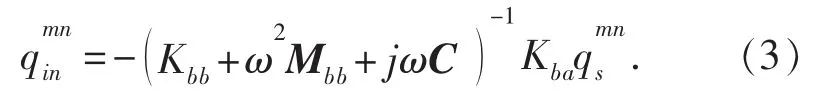
结合式 （2） 和式 （3） 可获得关系式 （4）， 式（4） 采用正六面体网格结构的有限元单元， 每个节点的位移都由三个方向 （u， v， w） 的位移合成，表示接触表面节点的载荷与位移矢量之间的关系[7]。

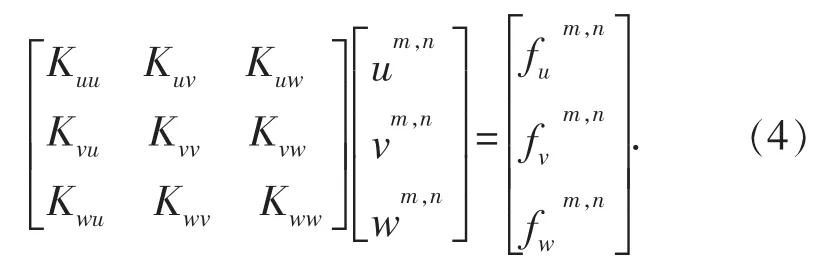
式中： um，n为接触面节点 X 轴方向位移向量； vm，n为接触面节点Y 轴方向位移向量； wm，n为接触面节点Z 轴方向位移向量；为接触面节点X 轴方向载荷向量为接触面节点Y 轴方向载荷向量为接触面节点Z 轴方向载荷向量；为系数矩阵中第s 行r 列的元素值。

薄板和周期性阻尼块在接触面节点处没有相对位移， 因此接触面节点位移矢量和载荷矢量中的元素可表示为

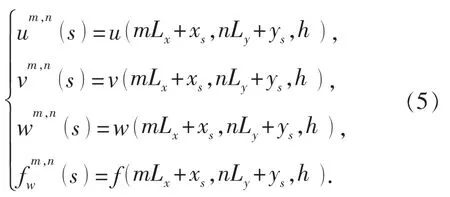
接触面节点力和节点位移之间的关系式为

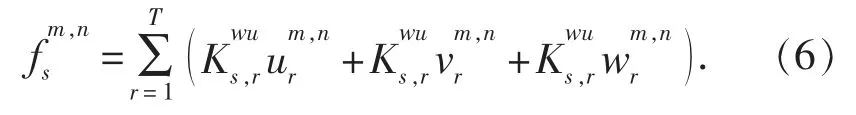
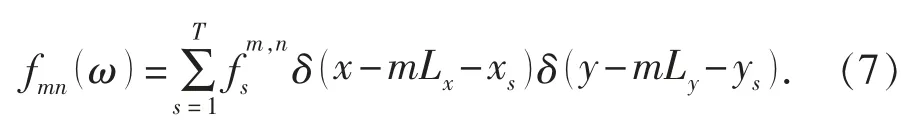
式中： δ 为狄拉克 δ 函数。

1.2 隔声辐射理论

将式 （7） 代入式 （1） 可以得到薄板的振动位移表达式为

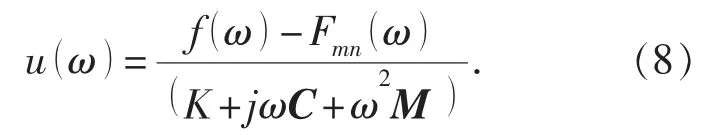
通过在式 （8） 的两侧求导获得一阶导数可以得到薄板表面的法向振动速度分布u'(ω) 。 根据薄板表面任意一点rs的法向振动速度瑞利积分，获得空间声场的辐射声压表达式为

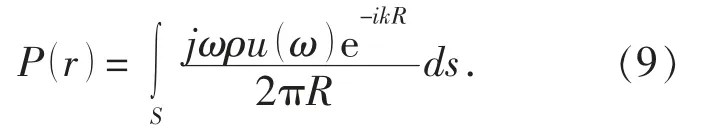
式中： R 为声场任意一点到薄板上点 rs的垂直距离[8]。

对式 （8） 求导以获得薄板表面的法向振动速度u'(ω )， 并将其代入式 （9）。 也就是说， 空间中任何一点的声压与刚度、 频率、 阻尼和质量之间的关系为

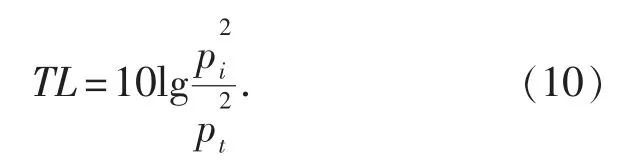
式中： pi为入射声压； pt为透射声压。

将式 （9） 代入式 （10）， 并结合前述得到的振动位移， 可以得到薄板的隔音量。

2 仿真结构模型的建立

首先建立二维周期阻尼薄板的UG 模型， 见图2； 然后将UG 模型导入Hypermesh 中进行网格划分， 见图3； 再添加约束， 利用声学仿真模拟软件建立仿真模型， 见图4， 并对敷设二维周期阻尼的薄板结构进行模态分析。

图2 二维周期阻尼结构UG 模型

图3 敷设二维周期阻尼薄板结构有限元模型

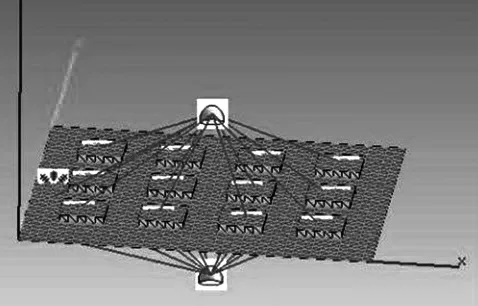
图4 二维周期阻尼结构仿真模型

3 仿真结果以及分析

3.1 阻尼块密度对隔声量的影响

图5 反映了阻尼块对隔声量的影响。 由图5 可知， 在 250～1 000 Hz 频率范围内， 由阻尼块密度增加引起的隔音效果不明显。

由于整个二维周期性阻尼薄板结构中散射体的质量较小， 图中曲线平缓且隔声量较小， 但进一步分析曲线可发现， 随着散射体密度的增加， 隔音带隙的起始和终止频率也在增加， 因此如果隔音间隙变宽， 可以在很大的频率范围内获得更好的隔音效果。

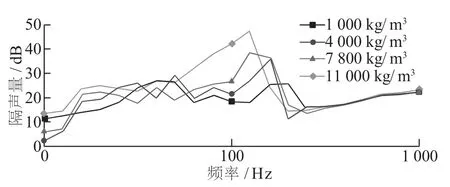
图5 阻尼块对隔声量的影响

3.2 阻尼块刚度对隔声量的影响

图6 反映了阻尼块刚度对隔声量的影响。 由图6 可知， 随着阻尼块弹性模量的增加， 隔音量在10～100 Hz 频率范围内减小， 并且在 100～1 000 Hz频率范围内几乎不变， 且隔音带隙的起止频率都没有明显变化。

出现这种现象的主要原因是阻尼块的材料是钢， 而刚性块的弹性模量明显不同于硬质橡胶， 所以， 阻尼块的弹性模量并不是隔音量的主要影响因素， 可以直接忽略。

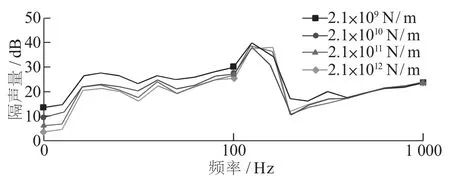
图6 阻尼块对隔声量的影响

3.3 晶格常数对隔声量的影响

图7 和图8 反映了晶格常数对隔声量的影响。从图7 和图8 可以看出， 所研究的薄片在X 轴方向上的薄板长度大于在Y 轴方向上的薄板长度。在X 轴方向上增加晶格常数对隔音量的影响明显小于在Y 方向上增加晶格常数对隔音量的影响，而不断增加晶格常数， 并不一定利于隔音。 如果增加晶格常数， 单元结构阻尼填充率就降低。 从图中也可以看出增加晶格常数对隔音带隙的起始和终止频率没有影响。

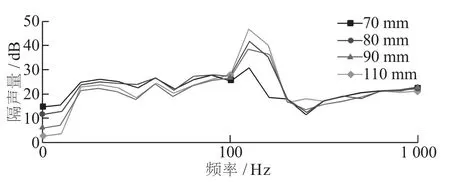
图7 X 轴晶格常数对隔声量的影响

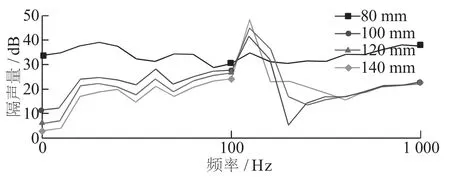
图8 Y 轴晶格常数对隔声量的影响

4 结论

1） 阻尼块密度增加引起的隔音效果并不是很明显， 但散射体的密度增大， 隔声带隙的宽度得到了扩展。

2） 阻尼块的弹性模量并不是隔音量的主要影响因素， 可以直接忽略。

3） 晶格常数对隔声量的影响： 增加X 轴方向上的晶格常数不如增加Y 轴方向上的晶格常数更能增强隔音， 同时增加晶格常数对隔音带隙的宽度没有影响， 且增加晶格常数对增加二维周期性结构的隔音没有太大影响。