GNSS时间序列小波降噪模型分析研究*

徐小汶，邓永春

（安徽理工大学测绘学院， 安徽 淮南 232001）

全球导航卫星系统 （Global Navigation Satellite System， GNSS） 对变形体观测数据经基线解算得到的移动站坐标序列即为GNSS 时间序列。 变形监测中的变形信息是期望获取有用的信息， 噪声误差是测量噪声过程中产生的多种不可控因素的集合。GNSS 测量噪声普遍存在， 包括外界环境、 观测人员自身、 仪器特性等引起的测量误差。 测量噪声时GNSS 时间序列中的变形序列信息与测量噪声信息相互混叠， 严重影响了变形信息的获取， 更不利于对变形信息的分析和预测。

GNSS 短基线解算过程中， 载波相位差分技术[1]使得测量误差中的对流层误差、 卫星钟差、 电离层误差、 相对论效应等都可以消除或者忽略不计相对较小的误差， 但是产生原因复杂多变的多路径效应却无法通过差分计算来消除[2]， 于是在GNSS 变形监测解算的时间序列中会出现测量误差信息与变形体的变形信息相互混叠， 难以区分的状况。 测量误差的信息阻碍变形信息的提取， 所以将GNSS 时间序列中的噪声和多路径误差信息提取出来预测变形信息至关重要， 只有将这些误差信息剔除， 才能提取GNSS 时间序列中的净化变形信息。

多年来， 针对如何净化变形监测数据的问题，国内外众多专家学者提出了很多方法， 主要包括：李德仁等[3]在测量平差的基础上， 用数理统计的方法将粗差归入随机模型， 提出用定权的方法对观测数据进行定权减小粗差甚至消除粗差的影响； 欧吉坤等[4]在周江文研究的基础上对真误差进行研究，求解真误差的秩亏方程， 对测量数据分群， 依据分群特征检测测量数据中的粗差； 吴富梅[5]等在对GNSS 时间序列信号进行频谱分析的基础上对GNSS中的粗差进行偏差探测， 辨别和剔除粗差； 於宗俦等[6]、 张正禄等[7]在基于控制网多余观测值足够多的情况下， 提出了多维粗差探测与定值的方法， 从而分辨和去除粗差； TSUCHIDA M 等[8]使用卡尔曼（Kalman） 滤波器， 通过改变参数， 处理可以解释主要由实际SAR 图像中的散斑产生的噪声和反向散射波的统计特性的变化， 降低实验中的图像噪声；杨汀等[9]根据对实际观测数据的分析， 对实际接收机和观测条件等建立不同的随机模型进行比较， 使近似模型与真实数据尽可能相似， 间接达到对实验数据降噪的效果； AINSLEIGH P L 等[10]基于缩放小波基表示各种信号， 用于脉冲噪声的时间序列数据和具有多径干扰的传递函数数据， 小波的时间和频率定位能力提供了更好的噪声检测和更少的信号失真， 在去除结构化噪声时表现更优； 刘凯[11]在处理混沌时间序列信号时的噪声问题， 将混沌信号和动力学系统看作是一个多维状态矢量， 提出一种基于粒子滤波的降噪算法， 这种降噪方法在最优估计的基础上实现对混沌信号的降噪， 降噪效果较优秀。戴吾蛟等[12]基于数据本身在空间域中对数据本身进行分解， 剔除GPS 数据中的强噪声即白噪声， 极大限度地去除测量数据中的随机误差， 从而提取更精确的多路径模型。

1 小波去噪原理

1980 年， 随着函数图像的伸缩和平移变换，小波分析及其应用逐渐出现。 小波分析方法随着Fourier 变换的发展逐步为人们熟知。 小波变换是一种能够对GNSS 时间序列时域和频域同时进行分析的方法， 在某种程度上小波分析方法可以通过函数的伸缩变换改变GNSS 时间序列的频域及时间窗的大小， 从而达到分离噪声的目的。 小波降噪最早由Weaver 等人开创性地提出， 在此基础上Donoho教授系统性地对小波降噪进行了研究， 完善了小波的降噪体系。 小波变换通过将GNSS 时间序列逐层分解分析并提取有用的信息从而达到降噪的目的。

1.1 小波基的选取

选取不同的小波函数基会对GNSS 时间序列降噪效果产生不同的影响， 最合适的小波基是将GNSS 时间序列信号经过小波变换后使小波的振动幅值趋近于0。 现今很少有文献研究小波基选取的最优方案问题， 大多都是通过反复试验或者利用经验积累选择合适的小波基， 对小波基的选择Nason等也提出了一套行之有效的方法， 但是这种方法在选取合适的小波基时， 计算量太大， 无法完全适用实际中的GNSS 时间序列降噪。 目前常用的小波函数有 db 系列小波、 bior 系列小波、 morlet 小波、sym 系列小波、 harr 小波函数等。

1.2 阈值函数

1） 硬阈值函数。 函数表达成保留大于或等于阈值的小波系数， 去除小于阈值的小波项。 硬阈值函数可表示为

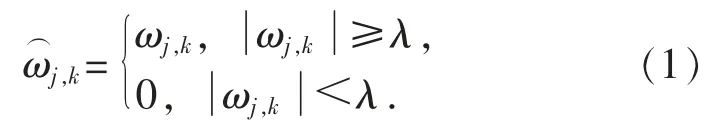
2） 软阈值函数。 函数将大于阈值函数的小波系数按照小波系数的比例缩小， 去除小于设定阈值的小波项。 其函数可表示为

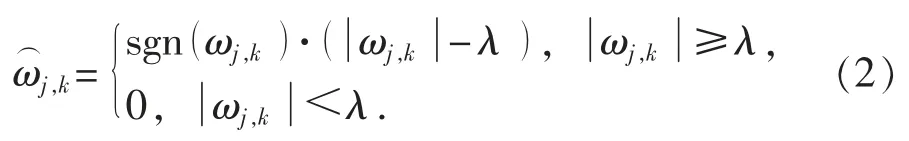
3） 软硬阈值折中函数。 软硬阈值折中函数的表达式为

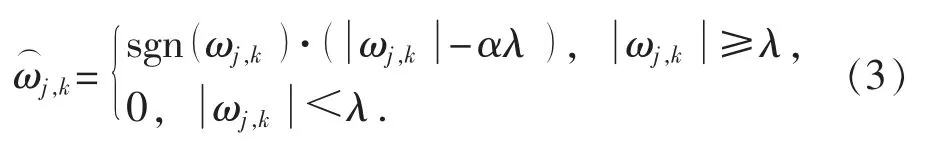
软硬阈值折中函数在软、 硬阈值函数的基础上加以修改， 将函数大于阈值函数的小波系数按照小波系数的α (0≤α≤ )1 比例缩小。 当 α=0 时， 该函数就是硬阈值函数； 当α=1 时， 该函数就是软阈值函数； 当0＜α＜1 时， 软硬阈值折中函数的取值就会处于软阈值函数和硬阈值函数之间。

1.3 阈值选取

影响GNSS 时间序列降噪效果的关键因素之一是小波阈值的合理设定。 如果小波阈值取得过小，即使GNSS 时间序列中的时间序列信息不丢失， 小波对时间序列中噪声的处理也不会将噪声完全滤除； 如果小波阈值取得过大， 即使能够完全滤除噪声， 但也会滤除一些GNSS 时间序列的有用信息，导致GNSS 时间序列中的有效信息丢失。 因此， 对GNSS 变形序列降噪时， 应选取合适的小波阈值，既能达到消除GNSS 时间序列噪声的目的也能达到保留GNSS 时间序列中有效信息的作用。

随着专家学者对小波阈值降噪的深入研究， 小波阈值的选取方法也在不断发展与更迭， 选取小波阈值的典型方法主要包括： 统一阈值、 Levelshrink阈值、 Sureshrink 阈值、 GCV 阈值、 Bayeshrink 阈值等。 小波阈值降噪的流程见图1。

图1 小波阈值降噪流程图

GNSS 时间序列小波降噪的具体步骤如下。

1） 小波分解： 选择合适的小波基， 对含噪的GNSS 时间序列进行小波分解， 得到各个尺度上的小波系数；

2） 作用阈值过程： 对各个尺度的信号进行非线性阈值降噪处理， 滤去小波系数为0 的小波项；

3） 小波重构： 降噪处理后的GNSS 时间序列小波系数， 得到降噪后的GNSS 时间序列系数。

2 降噪模型的评价指标

本文将采用偏差、 标准差、 信噪比和相关系数等指标对GNSS 时间序列多路径误差降噪模型进行评价。

2.1 偏差

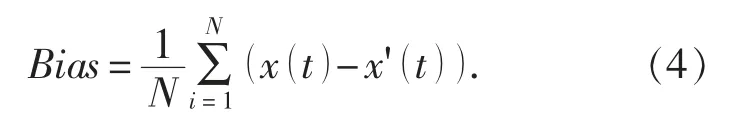
式中， Bias 为偏差， 其他同上。 Bias 为降噪后的时间序列与真实的时间序列间的偏差， 其数值越小，对时间序列的降噪效果越好。

2.2 信噪比

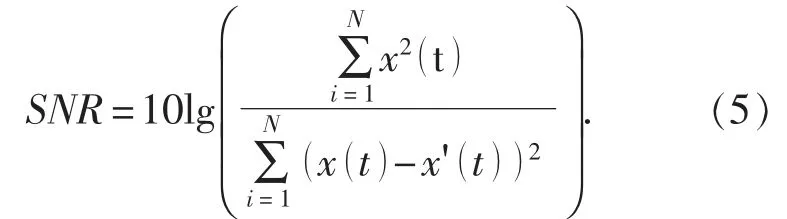
式中， SNR 为信噪比； N 为时间序列长度； x(t) 为带有噪声的原始时间序列； x'(t) 为降噪后的时间序列。 SNR 数值越大， 对时间序列的降噪效果越好。

2.3 相关系数

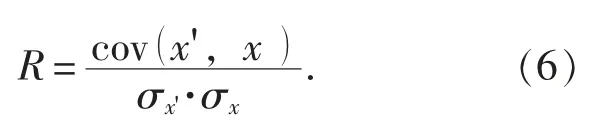
式中， R 为降噪前后时间序列的相关系数， 其他同上。 R 的数值越大， 对时间序列的降噪效果越好。

2.4 均方根误差

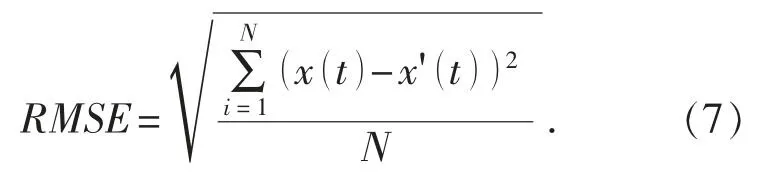
式中， RMSE 为降噪前后时间序列的均方根误差，其他同上。 RMSE 的数值越小， 对时间序列的降噪效果越好。

3 降噪模型的仿真模拟实验

为更好地解析各种降噪模型对时间序列降噪的效果， 采用仿真模拟实验验证各种降噪模型的降噪效果。 仿真时间序列降噪实验： 仿真一个时间序列真值， 然后在真值的基础上添加噪声模拟真实测量获得的时间序列， 应用各种降噪模型对时间序列进行降噪处理。

采用Matlab R2016a 软件进行仿真模拟实验，仿真白噪声 e（0， 12）。 函数构造如下， y_true 仿真时间序列， 主要包含频率为： 0.001 Hz， 0.002 Hz，0.003 Hz， 0.005 Hz； y 为仿真的包含白噪声的信号， 设置2 000 个历元， 仿真代码如下。

e=normrnd (0,1,1,2000) ;

y_true=sin (3*pi*t/1600) +sin (2*pi*t/500) +sin (5*pi*t/800) +sin (4*pi*t/400) ;

y_mix=y_true+e;

仿真原始信号和噪声信号见图2。 图3 为混合后的信号频谱。

小波基选择 haar 小波、 db5 小波、 coif4 小波，小波阈值选择3 和5， 过程略去， 其结果对应4 个检验指标 （见表1）。

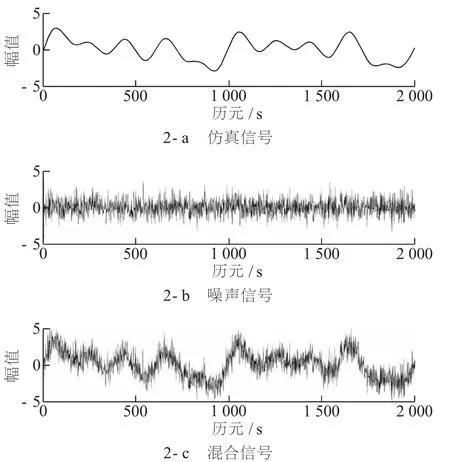
图2 仿真信号及噪声信号

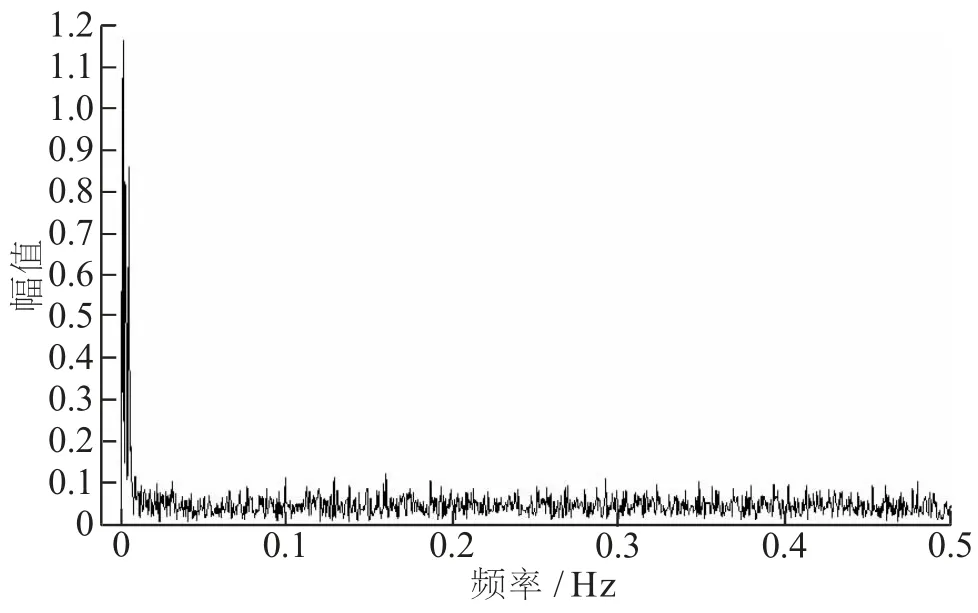
图3 混合信号的频谱特征

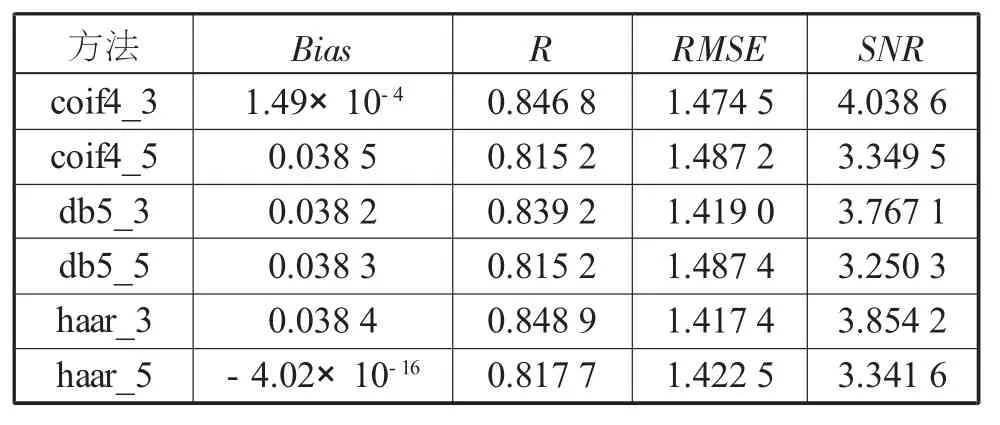
表1 降噪模型的4 个评价指标对比

从表1 可以看出， 总体上： 阈值为3 的小波降噪时间明显比阈值为5 的小波降噪效果好， 信噪比均优于阈值为5 的小波； 对于不同的小波基降噪模型的降噪效果， haar 小波基降噪模型优于db5 的降噪模型； coif4 小波基降噪模型降噪效果优于db5 小波基降噪模型。

4 实测数据实验

仿真数据已知真值， 且可以进行重复测试， 结果具有统计意义， 可以有效地检验算法的性能； 但是相关算法的优劣， 对于实际问题， 表现是否与仿真结果表现一致， 尚需采用实测数据分析。

4.1 数据采集

GNSS实验的是在某大学楼顶利用两台中海达V9 型号接收机进行数据采集， 采样间隔为1 s， 卫星高度角设置为10°， 采样时间为2018 年5 月17日， 年积日为136。 数据采集时天气晴朗， 无明显风感， 昼夜温差小。 对观测数据进行单历元基线解算， 解算结果为大地坐标系下的E/N/U 结果， 原始坐标序列见图4， 图中降噪方法从上到下依次为：原始E 方向序列、 N 方向序列、 U 方向序列。

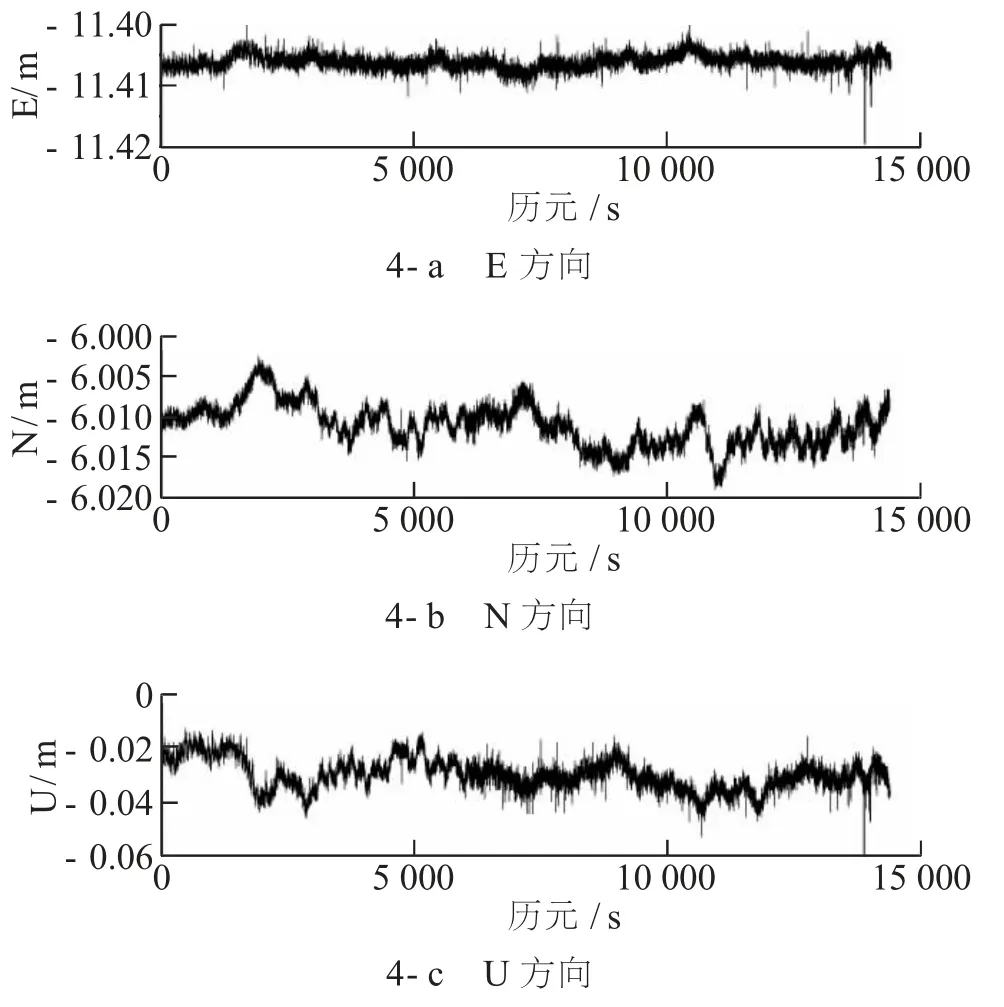
图4 原始坐标序列

4.2 实验结果与分析

采用不同方法， 以年积日136 的E 方向为例进行数据解算， 对结果进行降噪处理， 各种降噪效果见图 5， 对得到的信噪比、 偏差、 相关系数、 均方根误差4 个检验量进行比较， 见表2。

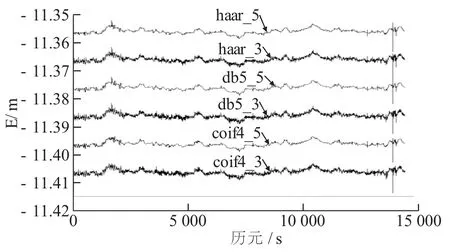
图5 6 种方法降噪后的坐标序列

由上述图表可得： 阈值为3 的小波降噪后， 其序列的4 项评价指标均优于阈值为5 的小波降噪评价指标； 在降噪效果上均服从仿真实验结果； 各类小波降噪方法并不能处理强噪声的情况。

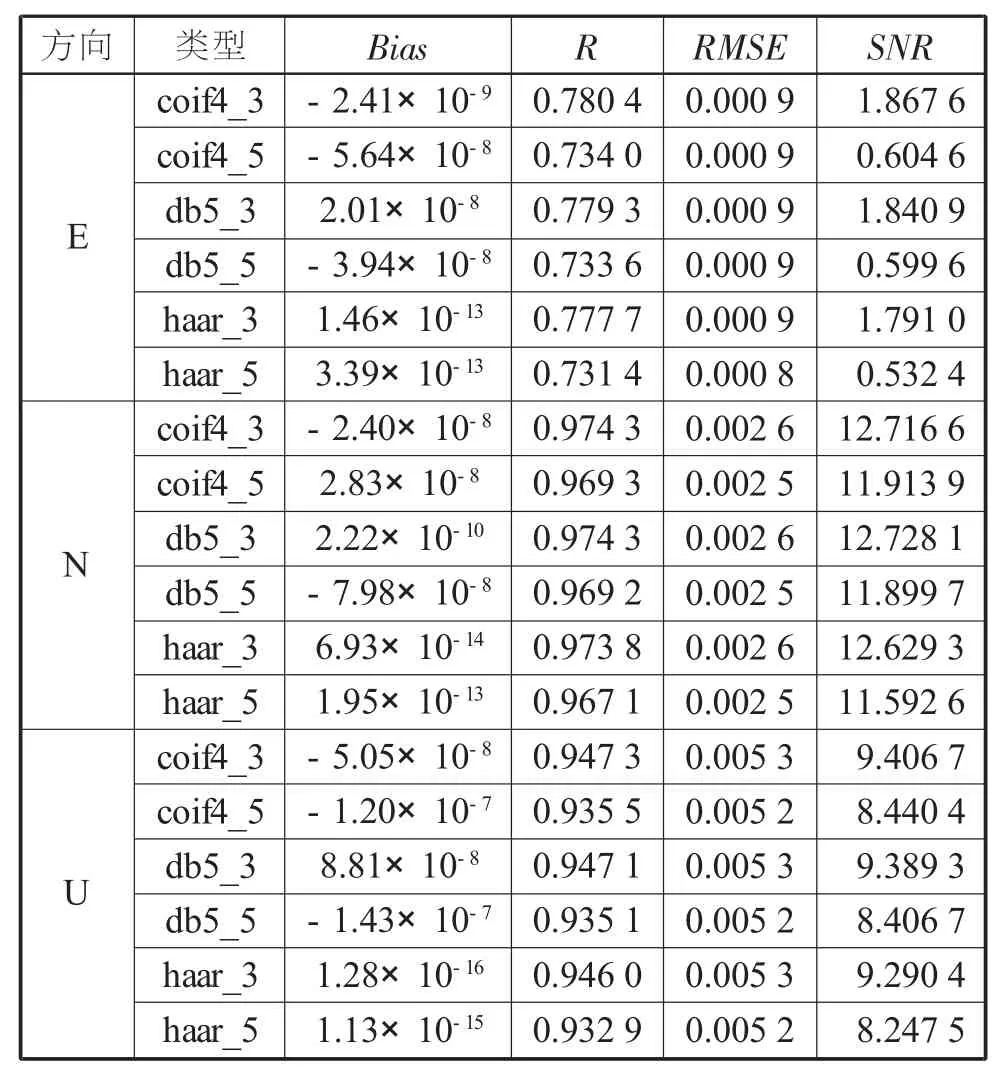
表2 降噪模型4 个评价指标对比

5 结束语

GNSS 时间序列中包含多种信息的多路径误差和变形信息， 同时GNSS 时间序列中也包含噪声信息， 噪声的存在严重影响到变形信息中的特征提取。 本文采用仿真实验和实测数据相结合的方式验证多种降噪模型的降噪效果， 通过三角函数仿真GNSS 坐标序列， 用随机噪声和高斯白噪声仿真高频噪声， 基于各类小波方法对序列进行降噪处理。主要结论如下： 实验结果表明haar 小波优于db5 小波， db5 小波优于coif4 小波， 小波阈值5 的时间序列降噪效果略优于小波阈值3 的时间序列降噪效果， 但设置阈值较小的小波方法， 阈值3 的运算时间更短， 计算效率更优秀； 小波降噪的方法是基于小波基函数， 所以在固定小波基函数的情况下无法抑制强噪声。

从上述结论可以看出， 小波降噪无论在仿真数据还是原始GNSS 序列中的降噪应用效果是明显的，但自适应小波基函数的选择问题是后期工作的努力方向。