考虑电磁力影响的四分裂导线舞动

蔡萌琦, 周林抒, 杨晓辉, 伍 川, 刘小会

(1.成都大学建筑与土木工程学院, 成都 610106; 2.四川省电力工业调整试验所, 成都 610016; 3.国网河南电力科学研究院, 郑州 450000; 4.重庆交通大学土木工程学院, 重庆 400074)

输电线路的导线舞动是一种频率低、长时间的振动,通常会引起短路、导线及金具失效、甚至杆塔倒塌等严重问题,通常会造成供电中断[1-2]。然而,对舞动的行为缺乏深入的了解,阻碍了有效的防舞技术的发展[3-4]。在过去的几十年中,由于气候变化和多分裂输电线路的广泛应用,导线舞动现象越来越频繁,引起了电气工程领域研究人员和设计人员的广泛关注。

由于输电线路特别是分裂导线舞动行为的复杂性,因此很难对所有线路进行试验研究。同时随着计算机的发展,数值方法成为有效和常见的研究手段。秦力等[5]提出了研究覆冰单分裂导线舞动特性的数值计算方法。近年来,有限元方法已成为研究舞动现象的一种有效方法。严波等[6-7]提出了研究覆冰双、三分裂导线舞动行为的数值方法。Hu等[8]在ABAQUS有限元软件中通过释放欧拉梁单元的弯曲自由度来模拟覆冰四分裂导线的舞动,并讨论了子导线周围的尾流对舞动特性的影响。严波等[9]和Yan等[10]针对四分裂导线舞动的内共振现象进行研究。刘小会等[11]研究了线路舞动时发生的内共振现象,并提出频率计算公式,可以获得连续档线路的模态函数。Cai等[12]用数值方法模拟的舞动结果验证了有限体积法确定的空气动力系数在覆冰四分裂导线舞动分析中的有效性。Zhou等[13]和周林抒等[14]首次研究了薄覆冰八分裂导线在均匀流场中的导线舞动行为。蔡萌琦等[15-16]分别针对扇形覆冰和湍流场中的八分裂导线舞动特性进行分析。上述导线舞动的研究均未考虑导线间电磁力的影响。

Mehta和Swart[17]提出一种方法来测定空间中任意形状和数量的导线之间的电磁力。Vastetsky[18]考虑了由大截面弯曲导线产生的三维电磁场,进一步采用渐近法建立的公式来计算三维电磁力。Liu等[19]研究了弯曲导线的电磁力和表面温度分布特性。周林抒等[20]研究了双分裂导线的粘连,发现这种现象主要是由电磁力引起的。伍川等[21]利用ABAQUS软件研究了电磁力对覆冰双分裂导线舞动特性的影响。

如前所述,在导线驰振过程中,分裂导线之间同时也会受电磁力的影响。四分裂导线输电线路在不考虑工作电流的情况下,其舞动特性同实际四分裂导线输电线路相比有所不同。然而,目前考虑电磁力影响下输电线路舞动的研究非常有限。

采用有限元软件ABAQUS中的UEL子程序,对考虑电磁力的四分裂导线舞动问题进行数值计算。进而,详细讨论在不同电流、档距和风速情况下,典型四分裂导线输电线路舞动特性。研究结果可为分析电流作用下的导线舞动现象提供依据。本研究可为数值结果的实际应用提供有利的参考和理论依据,同时也为架空输电线路研发有效的防舞技术提供参考。

1 考虑电磁力的输电线路舞动的数值模拟方法

给出在有限元软件ABAQUS中建立的子导体之间电磁力的数值计算方法。利用该方法,可以方便地将电磁载荷应用于研究分裂导线的舞动响应。

1.1 子导体间电磁力的计算

在实际风场中,正常电流条件下的四分裂导线各子导线之间会产生电磁引力[20-21],如图1(a)所示。假设两根无限长的、近似直线和平行的导线在箭头所示的方向上承载电流I1和I2,如图1(b)所示。如果导线之间的距离为d,则由于导线B1无穷长q中的电流i1作用于B2的单元p上的单位长度电磁力为

(1)

式(1)中:μ0是导线所在介质的渗透性,为4π×10-7H/m[20,21]。

图1 分裂导线电磁力图解Fig.1 Illustration of electromagnetic force for bundle conductors

1.2 典型四分裂导线的数值模型

选择的导线型号为4×LGJ-400/50,直径为27.6 mm,杨氏模量为70.0 GPa,泊松比0.3,密度为3 835.7 kg/m3。假设新月形冰厚为12 mm,初始迎角设置为50°。每个安装间隔棒型号为FJZ-450,其重量为7.5 kg。档距为200 m的线路典型有限元数值模型如图2所示。在该工况下,400个单元用于离散每根子导线。现有文献已经证明,当每个导线单元的长度小于或等于0.5 m时,可以实现求解收敛[8-9]。所有自由度方向的阻尼比设置为0.5%[15-16]。通过释放两个弯曲自由度,得到用于模拟导体振动的具有扭转自由度的索单元。由于间隔棒相对于导线具有较大刚度,可以简化为方形框架,并采用空间梁单元进行数值仿真。舞动数值模拟中的气动系数采用文献[8]中的风洞试验结果。

图2 200 m档距覆冰四分裂导线有限元模型Fig.2 FEM model of iced quad bundle conductor line with 200 m span length

1.3 不同电流强度下四分裂导线的导线间距

研究不同电流强度作用下(150、300、500、750 A)四分裂导线在不同档距(200、300 m)下的导线间距。在重力作用下,档距分别为200、300 m的两条输电线路的弧垂分别为2.190、5.300 m。在200 m档距线路上安装4个间隔棒。同时,在300 m档距线路安装5个间隔棒。

利用ABAQUS有限元软件,采用1.1节所提出的计算分裂导线之间的电磁力方法,利用UEL计算电磁力,可以得到不同电流强度下线路的平衡状态。由于电磁力的作用,子导线相互吸引。图3所示为不同档距下随不同电流变化的最小导线间距。可以看出,在达到500、750 A电流下,200 m跨线的最小间距为0.429、0.407 m,300 m跨线的最小间距分别为0.395、0.339 m。值得一提的是,导线最小间距出现在导线整档的中点位置,且最小间距随电流强度和线路档距增大而减小。

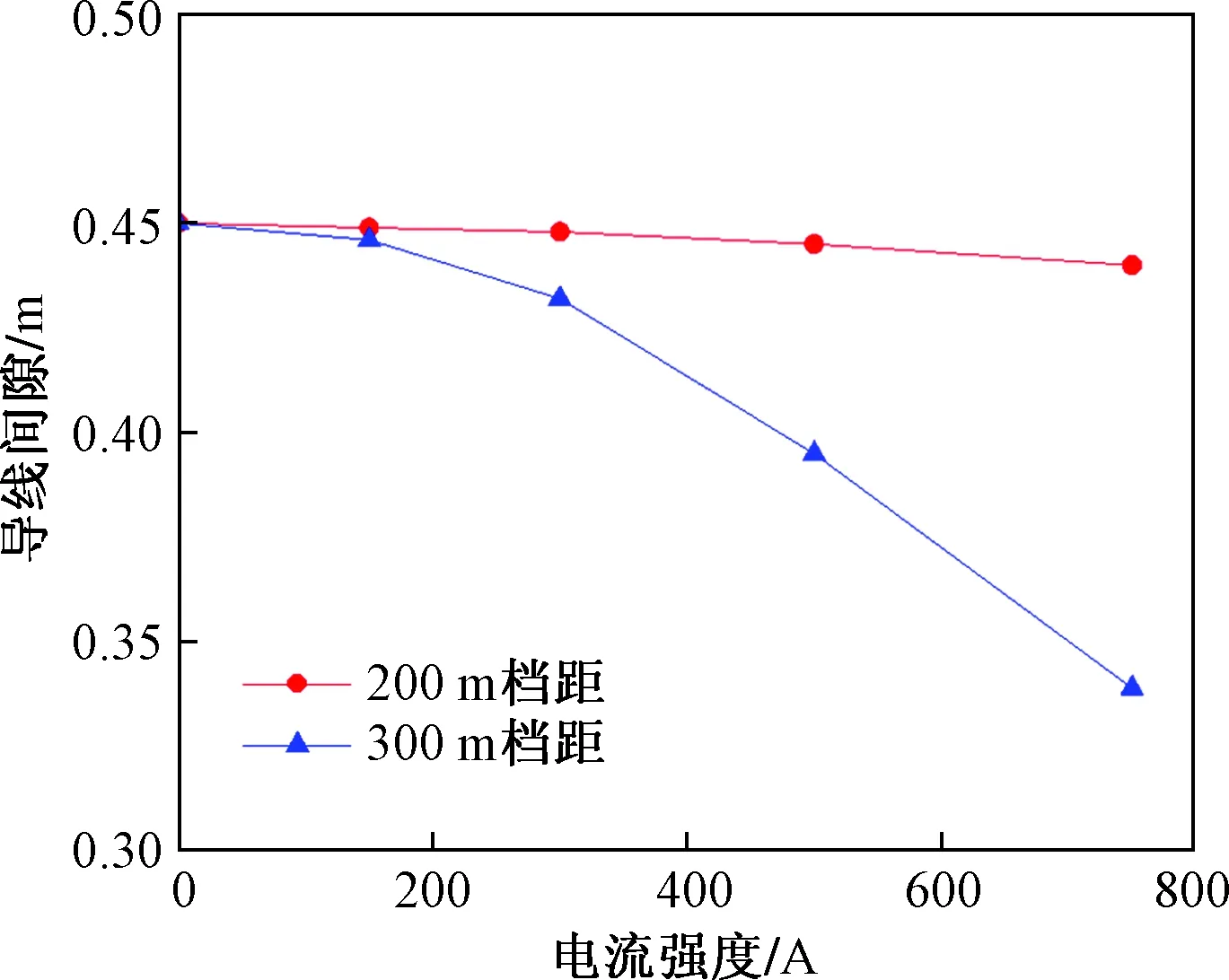
图3 随电流强度和档距变化的最小导线间距Fig.3 Minimum conductor clearance varying with current intensity under different span lengths

2 电磁力作用下输电线路的动态特性

分别研究不同档距的四分裂导线的动态特性,用以分析四分裂导线舞动。采用有限元方法得到200、300 m档距覆冰四分裂导线线路的垂直(平面内)、水平(平面外)和扭转方向的低阶固有频率和模态,如表1所示。

对于200 m档距输电线路,其第一阶对称平面外模式(单半波模式)的固有频率0.37 Hz小于平面内模式(单半波模式)的频率0.46 Hz。这意味着导线的平面内刚度大于平面外刚度。第一阶对称平面外模式(单半波模式)的固有频率0.37 Hz约等于第二阶平面内模式(双半波模式)的固有频率0.75 Hz和平面外模式(双半波模式)的固有频率0.75 Hz的1/2。第一阶对称平面外模式(单半波模式)的固有频率0.37 Hz约等于第三阶平面内模式(三半波模式)和平面外模式(三半波模式)的固有频率1.11 Hz的1/3。这意味着在这种情况下存在1∶2和1∶3的内部共振条件。同理,对于300 m档距输电线路,其线路固有频率和模态特性一样。在此,不再赘述。同时,对比可知,输电线路的固有频率随着档距的增加而减小。

为了分析四分裂导线在不同电流强度下的舞动特性,采用数值方法得到200 m档距线路在150、300、500、750 A的垂直(平面内)、水平(平面外)和扭转方向的低阶固有频率和模态,如表2所示。不同电流强度下200 m档距输电线路低阶的固有频率和振型模态一致,可以看出,电流强度对线路的动态特性没有明显影响。

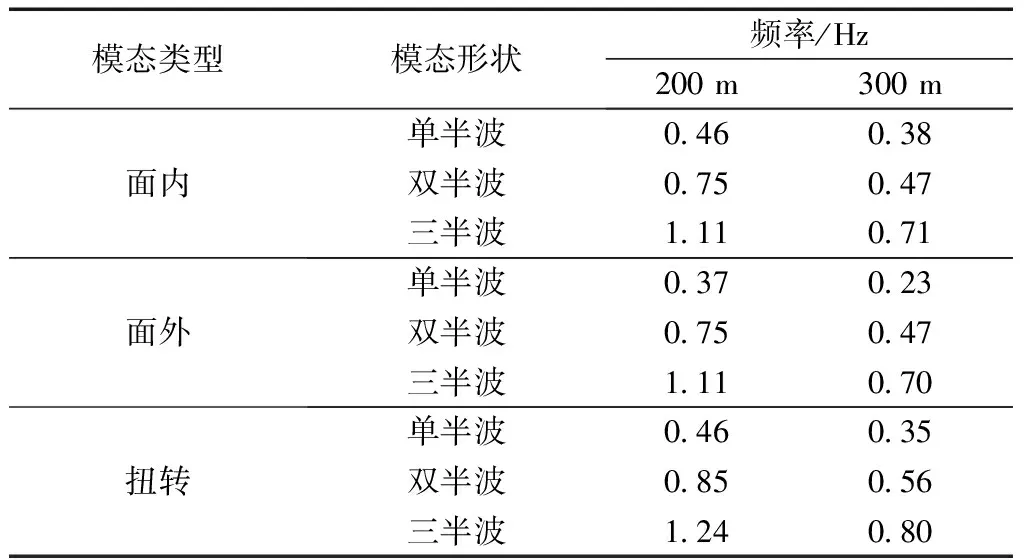
表1 四分裂导线在不同档距下的固有频率和模态Table 1 Natural frequencies and modes of quad bundle conductor line under different span lengths

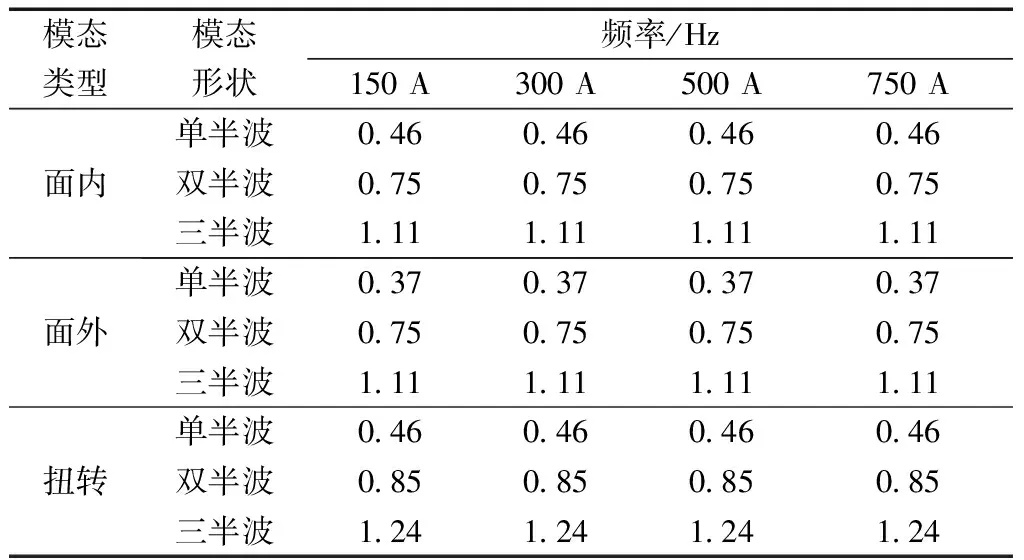
表2 四分裂导线在不同电磁强度下的固有频率和模态Table 2 Natural frequencies and modes of quad bundle conductor line under different current intensities

3 考虑电磁力作用下的四分裂导线舞动特性

利用本文提出的数值计算方法,可以用于预测在实际应用中电磁力的影响。考虑不同复杂工作条件(风速)、输电线路线路结构细节(线路档距)等主要因素,专门研究电磁力作用下的临界条件。这些参数对研究舞动特性和防舞技术的发展具有重要意义。

3.1 不同电流强度的影响

为了研究不同电流作用下(150、300、500、750 A)的300 m档距线路舞动的特性,图4给出了风速为12 m/s时300 m档距线路中点处的舞动轨迹。可以看出,不同电流强度下中点处的舞动轨迹较大差别,不同电流对300 m档距线路的舞动行为影响明显。由此可知,输电线路的舞动幅度随电流强度的增大而降低,这意味着导线间的电磁力将使舞动垂直幅度变小。

此外,随着电流强度的增加,导线的舞动轨迹变化会出现非线性振动模式。由图4(a)可知,在电流强度I=150 A时,线路舞动轨迹呈近似椭圆形。当电流强度达到300 A时,垂直方向的振动幅值变小,而水平方向幅值的变化增大[图4(b)]。当电流强度达到500 A时,垂直和水平方向的振动幅值均变小[图4(c)]。当电流强度达到750 A时,线路几乎不发生大振幅舞动[图4(d)]。同时可以看出,随着电流强度逐渐增大,舞动垂直振幅会随电流强度的增大而减小,且轨迹逐渐由椭圆逐渐过渡为异形。

图4 不同电流强度下四分裂子导线中点舞动轨迹Fig.4 Galloping traces of mid of quad bundle conductors under different current intensities

3.2 不同风速的影响

运行中的输电线路舞动观测表明,舞动通常发生在风速范围为4～20 m/s情况下。为了研究考虑电磁力作用下风速对新月形覆冰四分裂导线舞动行为的影响,选取典型风速12、14、16 m/s进行分析,在此取电流强度为750 A。对200 m档距线路在不同风速下的舞动过程进行模拟。图5显示了不同风速下新月形覆冰四分裂导线的舞动轨迹。随着风速的增大,舞动幅度明显增大,特别是在风速为16 m/s时[图5(c)]。该现象表明在较高风速下,线路更容易被激发高阶舞动模式[15-16]。

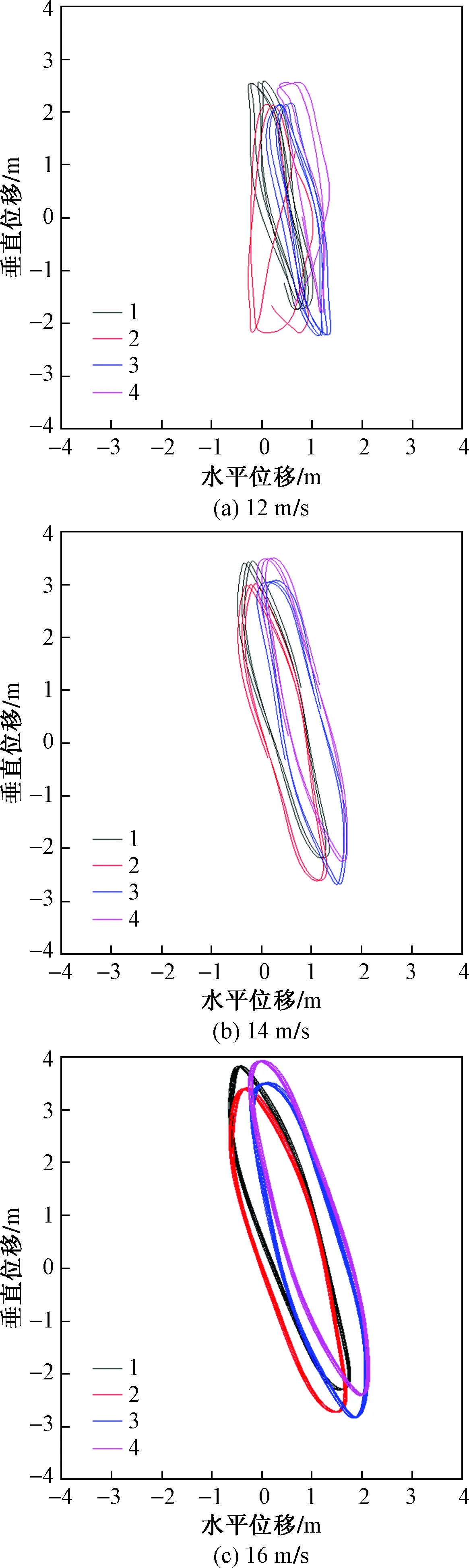
图5 考虑电磁力作用下不同风速下覆冰四分裂子导线中点的舞动轨迹Fig.5 Galloping traces of mid of sector-shape quad bundle conductors under different wind velocities considering electromagnetic forces effects

3.3 不同档距的影响

为了研究考虑电磁力作用下的不同档距(200、300 m)对覆冰四分裂导线输电线路舞动特性的影响,在此风速设置为12 m/s,电流强度为150 A。随着典型输电线路弧垂随档距的增大而增大,其舞动特性也通常会随着线路档距的增大而增大,大档距线路的舞动危险性也相应地上升。由图6可知,其垂直和水平方向的舞动幅值均随线路档距的增加而增大,说明在档距较长的线路上,舞动发生的可能性较大。且随着线路档距的增大,考虑电磁力作用下四分裂导线的舞动轨迹也呈现非线性变化,此现象是由于舞动是垂直和水平方向的耦合振动。可以得知,档距的增加也会致使线路发生高阶舞动。

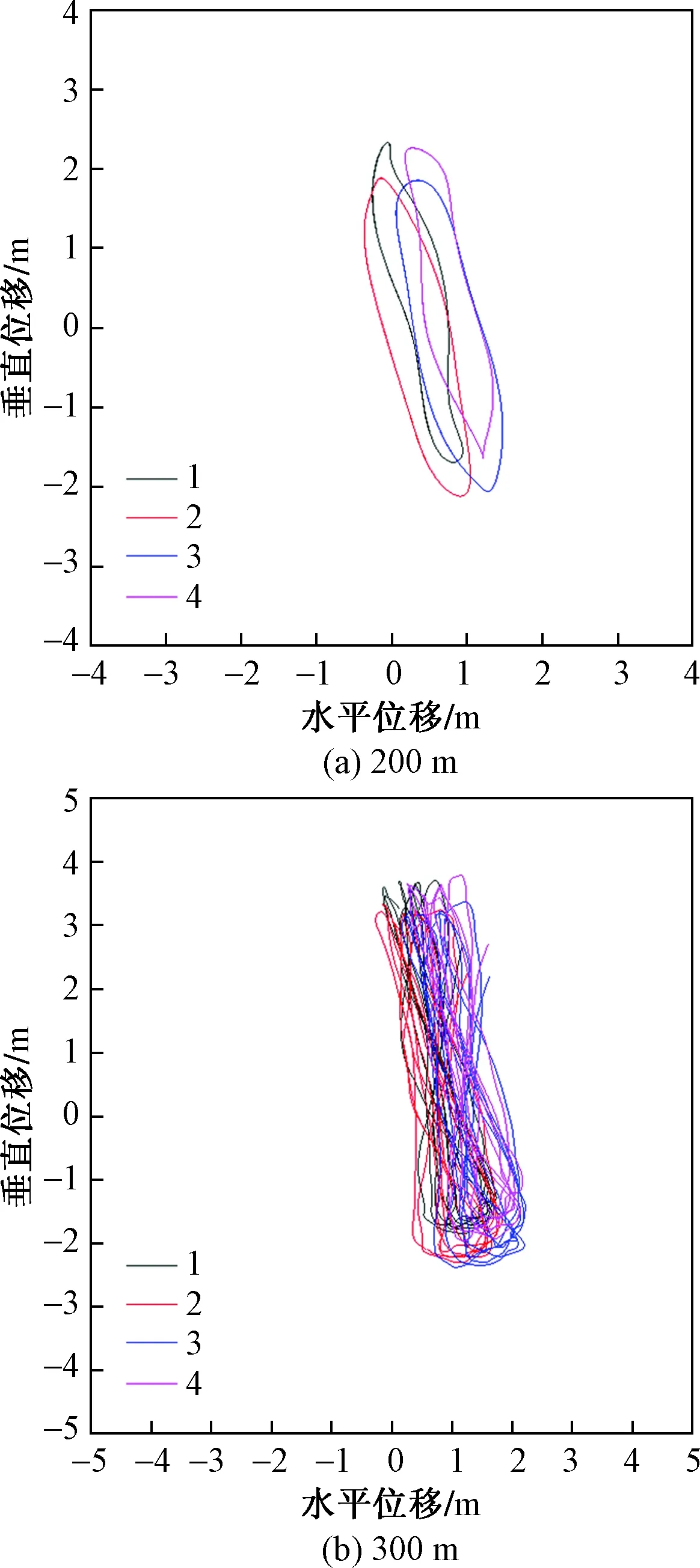
图6 考虑电磁力作用下不同档距下覆冰四分裂子导线中点的振动轨迹Fig.6 Galloping traces of mid of iced quad bundle conductors under different span lengths considering electromagnetic forces effects

4 结论

在有限元ABAQUS软件中,开发了一种考虑电磁力的用户自定义导线单元,用于模拟四分裂导线的舞动。利用有限元方法及其有效性,研究了覆冰四分裂导线输电线路的舞动特性。得到如下结论。

(1)电流对四分裂输电线路的动态特性几乎没有影响。

(2)电磁力会引起子导线之间的相互吸引,最小导线间距位于导线档距的中间,且最小间距随电流强度和线路档距增大而减小。

(3)舞动模式会随着电流强度的不同而变化。在固定线路档距和风速下,舞动垂直振幅会随电流强度的增大而减小。

(4)在相同的电流强度下,舞动模式会随线路档距和风速的不同而变化。导线舞动幅值随线路档距和风速的增大而增大。

(5)对舞动过程中电磁力的数值模拟方法可以推广到对其他分裂导线驰振研究的数值模拟。