授权模式下再制造生产和回收定价竞争策略
杨爱峰, 詹倩颖, 宋明珠
(合肥工业大学 管理学院,安徽 合肥 230009)
0 引 言
随着环境污染和资源短缺等问题日益突出,废旧品回收再利用受到了社会各界的密切关注。再制造是以产品全寿命周期理论为指导,以优质、高效、节能、节材、环保为准则,以先进技术和产业化生产为手段进行修复、改造废旧设备产品的一系列技术措施或工程活动。实践证明,再制造在节约资源、降低环境污染和增加企业效益等方面发挥着重要作用,是废旧物品回收再利用的有效方式之一。在实践中,再制造行业吸引了许多原始设备制造商(original equipment manufacturer,OEM)和第三方再制造商(第三方)进入[1]。然而,很多再制造过程本身并不破坏废旧品物理形态,仅对产品进行修复、替代或修理损坏的部件,使得再制造品保持原产品的外观和内部结构,甚至在再制造品销售中还要保留原产品的商标标识。第三方的再制造涉及到OEM的产品声誉、技术专利、消费市场抢占等问题,因此往往需要OEM授权才能进行废旧品的回收再制造[2]。这说明研究授权模式下,第三方和OEM在正向供应链销售市场和逆向供应链回收市场的竞争具有重要现实意义。
目前,已有大量文献研究了再制造的正向供应链销售市场和逆向供应链回收市场的竞争。关于正向供应链销售市场的竞争,文献[3]假设OEM通过授权或外包允许第三方进行再制造,OEM和第三方在生产量和销售价格上进行竞争,研究结果表明当消费者对再制造品的估值较低时,第三方偏好授权模式,否则偏好外包模式,且在这2种情况下OEM通过外包比授权能获得更高的利润;文献[4]研究了在OEM授权第三方再制造情况下,当新产品和再制造产品存在价格竞争时OEM和第三方的定价策略和协调策略;文献[5]假设在正向渠道制造商生产新产品,零售商按契约再制造并销售新产品和再制造品,且在逆向渠道零售商和第三方同时回收废旧品的情况下,研究结果表明,制造商在双渠道回收情况下能获得更多的利润;文献[6]考虑了在产品需求不确定和废旧品质量不确定情况下,2个再制造商通过共同的零售商销售他们的替代产品,且在价格和服务2个方面均存在竞争,研究结果表明当需求波动变大时,直销渠道相比其他渠道模式能提供更好的商品。
关于逆向供应链回收市场的竞争,文献[7]研究了OEM和第三方、OEM和零售商、零售商和第三方3种双渠道回收竞争模式,研究结果表明无论竞争强度的大小,对于OEM来说选择OEM和零售商双渠道回收竞争模式最优。文献[8]研究在制造商受专利保护的条件下,建立了含有一个能自行回收的制造商及一个具有再制造能力回收商的闭环供应链模型,研究结果表明,在再制品供不应求的市场中,只有当回收商再制造成本低于制造商时制造商才会授权其进行再制造。
此外,有些文献既研究正向供应链销售市场的竞争,又研究逆向供应链回收市场的竞争。文献[9]建立了OEM与第三方在回收市场中存在距离竞争以及新产品与再制造品存在价格竞争的2个阶段模型情形,研究结果表明销售市场竞争越激烈,越能促进第三方在回收市场更加努力,且对于OEM均有利;文献[10]在文献[9]的基础上,进一步假设OEM和第三方在销售市场和回收市场均存在距离竞争时,OEM和第三方的定价和回收策略;文献[11]基于新产品与再制造产品存在价格竞争以及制造商和再制造商存在回收竞争情形构建了两周期模型,研究并比较固定费用和单位授权费2种不同专利许可策略下供应链成员决策。
本文在已有研究基础上,假设第三方需要向OEM缴纳授权费才能进行回收再制造,并且在正向供应链销售市场中消费者对OEM生产的再制造品质量更为信赖,OEM和第三方通过再制造品零售价格抢占消费者市场。在逆向供应链回收市场上,消费者愿意将废旧品卖给回收价格更高的企业,OEM和第三方通过废旧品回收价格来激励消费者进行回收竞争。本文建立了以双方闭环供应链利润最大化为目标带约束条件的古诺博弈模型,通过K-T条件得出2个企业最优的再制造品生产量以及废旧品回收价格。最后通过解析方法分析了单位授权费、消费者中环保主义者主动无偿返还废旧品数量和废旧品残值对最优废旧品回收价格的影响,以及OEM和第三方再制造品单位生产成本对最优再制造品生产量的影响,并运用数值算例方法分析了上述参数对最优利润的影响。
1 符号说明及假设
1.1 符号说明
本文有关参数及决策变量如下:pi为企业i再制造品的单位零售价格;di为企业i再制造品的市场需求(决策变量);ai为企业i从消费者处回收废旧品的单位价格(决策变量);qi为企业i从消费者处回收废旧品的数量;ci为企业i再制造品的单位生产成本;s为OEM或第三方回收废旧品的单位残值收入;f为OEM授权第三方进行回收再制造的单位授权费;α为消费者中环保主义者主动无偿返还废旧品的数量;β为消费者对废旧品回收的价格敏感系数;θ为消费者对废旧品回收的交叉价格敏感系数,θ<β;δ为消费者对OEM生产的再制造品的支付意愿,服从[0,1]上的均匀分布;ρ为消费者对第三方和对OEM生产的再制造品支付意愿比值,ρ∈(0,1)。其中,i∈{m,t},m和t分别表示OEM和第三方。
1.2 假设
假设1第三方需要向OEM缴纳授权费才能进行回收再制造,OEM和第三方在正向供应链的销售市场通过再制造品零售价格进行竞争,在逆向供应链的回收市场通过废旧品回收价格进行竞争。
假设2OEM和第三方生产同种产品,消费者对OEM生产的再制造品质量更为信赖,当消费者对OEM生产的再制造品支付意愿为δ时,对第三方生产再制造品的支付意愿仅为ρδ。消费者购买OEM和第三方生产再制造品的效用分别为Um=δ-pm、Ut=ρδ-pt。当Um>0且Um>Ut时,消费者购买OEM生产的再制造品;当Ut>0且Ut>Um时,消费者购买第三方生产的再制造品。通过简单积分得到OEM的需求函数为dm=1-(pm-pt)/(1-ρ),第三方再制造品的需求函数为dt=(ρpm-pt)/[ρ(1-ρ)]。为计算简便,求得反需求函数分别为pm=1-dm-ρdt、pt=ρ(1-dm-dt),将再制造品的市场需求di作为决策变量。
假设3在逆向供应链回收市场中,废旧品回收数量不仅受自身回收价格影响,还受到竞争企业回收价格影响,但竞争企业回收价格对该企业回收数量的影响要小于自身回收价格的影响。因此假设OEM和第三方的废旧品回收数量分别为qm=α+βam-θat、qt=α+βat-θam。为计算方便,进一步假设β=1,即qm=α+am-θat,qt=α+at-θam,θ<1。
假设4 OEM和第三方必须满足消费者的再制造品需求,再制造品的生产量就是需求量。回收市场中废旧品数量充足,废旧品的回收量应不少于再制造品的生产量,即di≤qi。
2 模型构建与求解
在本模型中,OEM和第三方通过回收价格和生产量分别在逆向供应链回收市场和正向供应链销售市场进行竞争,两企业是古诺博弈关系。OEM和第三方同时决策各自废旧品的回收价格ai和再制造品的生产量di(i=m或t)。OEM和第三方的规划模型分别为:
maxdm,amΠm=pmdm-cmdm-amqm+
s(qm-dm)+fqt;
s.t.dm≤qm
(1)
maxdt,atΠt=ptdt-ctdt-atqt+
s(qt-dt)-fqt;
s.t.dt≤qt
(2)
其中,(1)式和(2)式目标函数的第1项分别表示两企业再制造品的销售收入;第2项分别表示两企业再制造品的生产成本;第3项分别表示两企业废旧品的回收成本;第4项分别表示两企业未进行再制造的废旧品的残值收入;第5项分别表示OEM的授权费收入和第三方的授权费支出;约束条件分别表示两企业废旧品的回收量不能低于再制造品的生产量。
命题1 设
(4-ρ)[2α-θ(f-α)+θ3f]};
ρ(4-ρ)[2f(1-θ2)-(2+θ)α]};
(8-3θ2)(ct+f)-ρ(2-θ2)cm+
αρ(7θ-2)+ρθ2f(2+θ)-
ρ2[α-θ(3-α)]};
2ct)-(2-θ2)[2(1+ρ)cm-ρct]-
θ2[(1+2fθ)(1+2ρ)-ρ2(2-α)+
ρ(3f-α-ρ-ρθf)]-
2(α-f)[ρ(1+2θ)+θ]}。
当s≥max{M1,M2}时,最优解为:
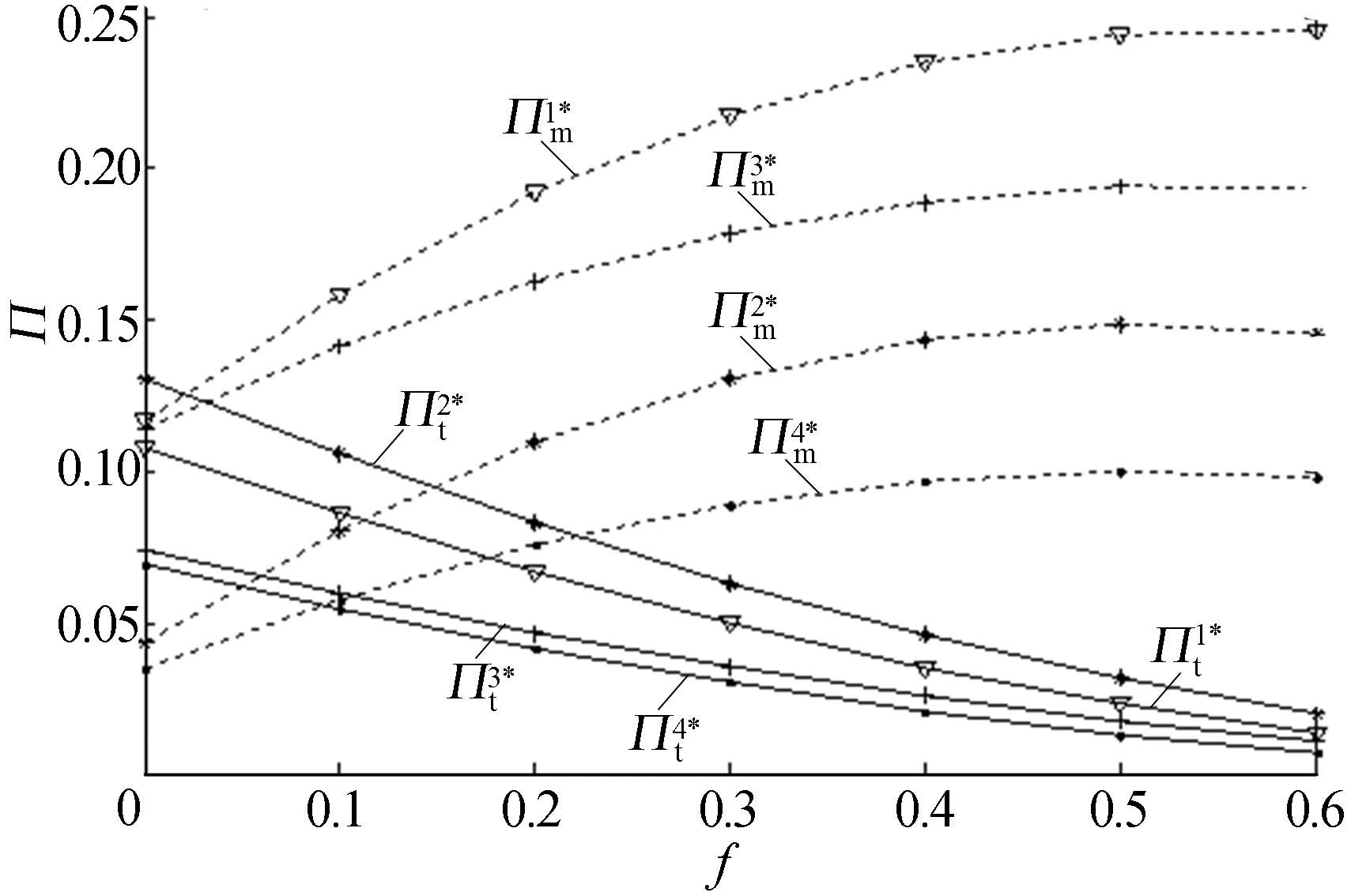
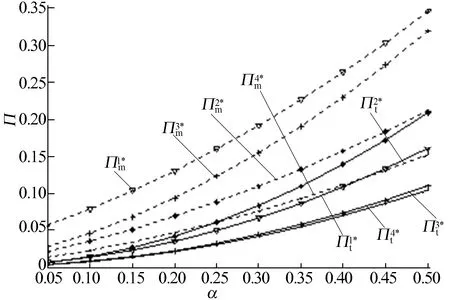
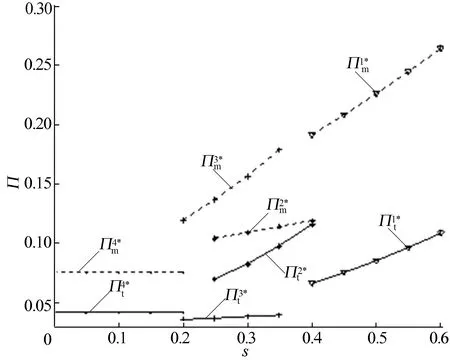
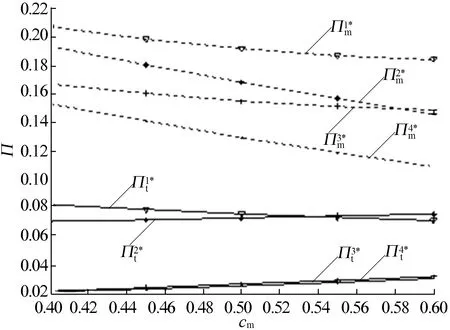
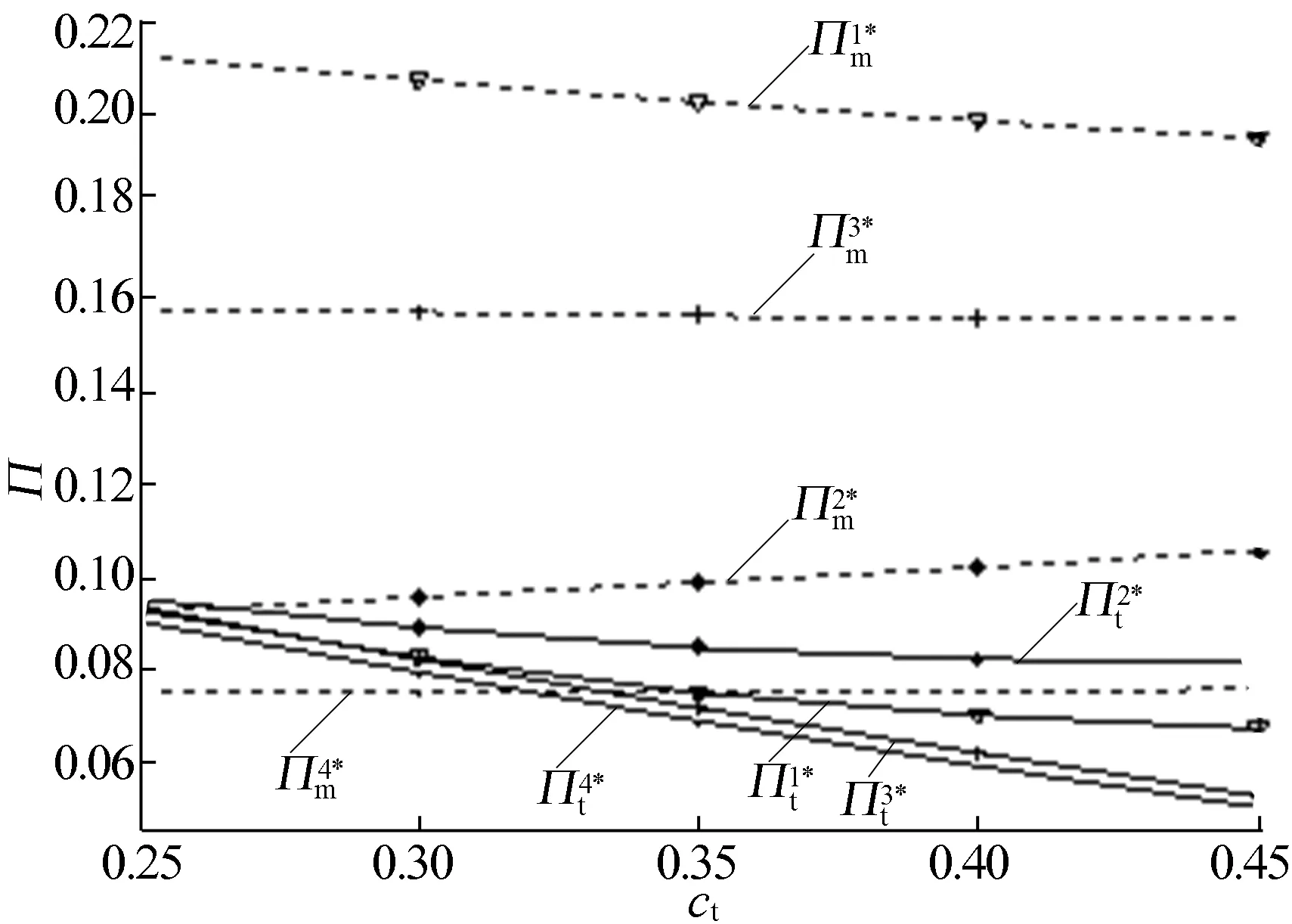
当M3≤s 2(ct-2cm+s+2-ρ)-4θf}/ [2(8-ρ)-θ2(6-ρ)], 2θ(θf+α)+θ(ct-2cm+s-2)]/ [2(8-ρ)-θ2(6-ρ)]; 4α-2θ[(1-θ2)f+s-α]}/ [2(8-ρ)-θ2(6-ρ)], 2θf[1-θ2)-2α(2+θ]}/ [2(8-ρ)-θ2(6-ρ)]-(s+ct)/2ρ。 当M4≤s θ(ρcm-2ct+ρ-6f)+ (4+ρθ)s-2α(2+θ)]/ [2(4-θ2)+ρ(2-θ2)(4-ρ)], -2(ct+f))+(2α-sθ)(ρ2-2)- (4ρ-ρ2+2)θ(θf+α)]/ [2(4-θ2)+ρ(2-θ2)(4-ρ)]; ρ[θ(α-s)+2(α-ct-f)+ θ2(ct+2f-ρ)-2ρ)]/ [2(4-θ2)+ρ(2-θ2)(4-ρ], 2[θ(α-s)+2α)-2f(1-θ2)]}/ [2(4-θ2)+ρ(2-θ2)(4-ρ)]。 当s (4-ρ)αρ(1+θ)-(2f+3α)θ+ (1-cm)(2ρ-ρθ+2)-3α(2+ρ)+ ρθ(1-2α+fθ)-ρ2], 2[2(ct+f+α)-ρ+αθ]+ ρθ[2(f-2α)+ct-ρ(1-α)]+ θ(2ρ+1)(1-cm-α-θf)}; (1-θ2)[ρ(ct+f-ρ)-θf(1+2ρ)]+ θ[ct+ρ(α-1)]+α(θ+2+ρ)}, ρ(3+fθ+cm-α)+θ(3α-1+cm)- ρθ2(2+fθ+cm)+α(2-ρθ)]。 其中 A=(2+θ)[2-θ+(4-ρ)(1-θ)]; B=(2+θ)[(1-θ)ρ(4-ρ)+(2-ρ)(2-θ)]; C=ρ(4-ρ)(1-θ2)+8-3θ2+2ρ(2-θ2-θ); D=ρ(4-ρ)(1-θ2)-θ(2ρ+θ)+ 2(2-θ2)(1+ρ)+4。 证明根据OEM与第三方古诺博弈关系,同时求解am、dm、at、dt。首先对(1)式目标函数Πm分别求关于am和dm的Hessian矩阵为: 显然h11<0且|H1|=4>0,即Hessian矩阵负定。又因为其约束条件为线性约束,所以规划模型(1)是凸规划,因此K-T点为最优解。 同时对(2)式目标函数Πt分别求关于at和dt的Hessian矩阵,同理得规划模型(2)是凸规划,因此K-T点为最优解。 相应地,规划模型(1)、(2)的Lagrange函数分别为: L(am,dm,λ1)=pmdm-cmdm-amqm+fqt+ s(qm-dm)+λ1(qm-dm), L(at,dt,λ2)=ptdt-ctdt-atqt-fqt+ s(qt-dt)+λ2(qt-dt) 。 进而得到(1)式和(2)式的K-T条件分别为: (3) (4) 4(1-α)(1+ρ)+θ[ρ(1-α)-2ct]- ρ2(2-α)-2(α-f)[ρ(1+2θ)+θ]- θ2[(1+2fθ)(1+2ρ)+ ρ(3f-α-ρ-ρθf)]}, -ρ(2-θ2)cm-ρ2[α-θ(3-α)]+ ρθ(2cm-2-ct-3f)+ρθ2f(2+θ)+ αρ(7θ-2)}。 令λ1>0和λ2>0可得s的范围。命题1得证。 根据命题1的证明可知:当λ1=0和λ2=0时,意味着dm≤qm和dt≤qt,此时OEM和第三方都是部分再制造(简称MPTP);当λ1>0和λ2=0时,意味着dm=qm和dt≤qt,此时OEM是完全再制造,第三方是部分再制造(简称MFTP);当λ1=0和λ2>0时,意味着dm≤qm和dt=qt,此时OEM是部分再制造,第三方是完全再制造(简称MPTF);当λ1>0和λ2>0时,意味着dm=qm和dt=qt,此时OEM和第三方都是完全再制造(简称MFTF)。 推论1 对于OEM,在MPTP、MTPF、MPTF 3种情形下,从回收市场回收废旧品的单位价格am均随着单位授权费f的增加而减小,但在MFTF情形下,当ρ>5θ/(1-θ)2时,am随着f的增加而增加,当ρ<5θ/(1-θ)2时,am随f的增加而减少;对于第三方,在MPTP、MFTP、MPTF和MFTF 4种情形下,从回收市场回收废旧品的单位价格at均随着单位授权费f的增加而减少。 推论1表明,随着单位授权费的增加,第三方进行回收再制造变得越来越无利可图,因此第三方将降低废旧品的回收价格来减少从回收市场回收的废旧品数量,直至单位授权费高到一定程度时,第三方才与OEM解除授权关系而退出回收再制造。同时由于OEM和第三方在逆向供应链的回收市场是竞争关系,因此它将通过降低其废旧品的回收价格和第三方竞争。但是,在MFTF情形下,当ρ>5θ/(1-θ)2时,随着顾客对第三方生产的再制造品和OEM生产的再制造品的支付意愿比值的增加,OEM生产的再制造品在正向供应链的销售市场中越来越没有竞争力,OEM只能通过增加废旧品回收价格以回收更多的废旧品用于再制造获利。 推论2在MPTP、MFTP、MPTF和MFTF4种情形下,OEM和第三方从回收市场回收废旧品的单位价格ai(i=t和m)均随着消费者中环保主义者主动无偿返还废旧品数量α的增加而减少。 推论2表明,随着消费者中环保主义者主动无偿返还废旧品数量的增加,OEM和第三方就没有必要出高价格从回收市场那里回收废旧品。因此当消费者中环保主义者主动无偿返还废旧品的数量增加时,OEM和第三方均会降低废旧品回收价格。 推论3在MPTP、MFTP和MPTF 3种情形下,OEM和第三方从回收市场回收废旧品的单位价格ai(i=t和m)均随着废旧品残值s的增加而增加。但在MFTF情形下,ai(i=t和m)与s无关。 推论3表明,在MPTP情形下,OEM和第三方均采取部分再制造策略,随着废旧品残值的增加,双方均会通过增加回收价格从回收市场获得更多的废旧品,在满足正向供应链的再制造品需求后,可以获得更多的残值收益。在MFTP和MPTF情形下,OEM和第三方总有一个企业是部分再制造,另一个企业则是完全再制造,随着废旧品残值的增加,采取部分再制造的企业会通过增加回收价格从终端消费者处获得更多的废旧品,在满足正向供应链的再制造品需求后,可以获得更多的回收残值收益,而采取完全再制造的另一企业虽然不能从废旧品残值获得收益,但2个企业在逆向供应链的回收市场是竞争关系,故当其中一个企业提高废旧品回收价格时,另一个企业也会提高回收价格。在MFTF情形下,OEM和第三方均是完全再制造,所以双方均无法通过废旧品残值获得收益,因此废旧品回收价格不受废旧品残值影响。 推论4 在MPTP、MFTP、MPTF和MFTF 4种情形下,OEM再制造品的生产量dm均随着OEM再制造品的单位生产成本cm的增加而减小;第三方再制造品的生产量dt均随着OEM再制造品的单位生产成本cm的增加而增加。 推论4表明,随着OEM再制造品单位生产成本的增加,OEM将增加其再制造品的零售价格获利,此时消费者必然会降低对OEM再制造品的需求,因此OEM将减少再制造品的生产量。由于第三方与OEM在正向供应链的销售市场中是竞争关系,消费者会转向购买第三方的再制造品,从而会导致消费者对第三方再制造品需求量增加,因此第三方将增加再制造品的生产量。 推论5 在MPTP、MFTP、MPTF和MFTF 4种情形下,第三方再制造品的生产量dt均随着第三方再制造品的单位生产成本ct的增加而减小;OEM再制造品的生产量dm均随着第三方再制造品的单位生产成本ct的增加而增加。 推论5的结果与推论4类似,此处不再赘述。推论1~推论5的证明较易,只需对决策变量关于各个参数求导数来判断增减性即可,具体从略。 本节将通过算例分析单位授权费f、消费者中环保主义者主动无偿返还废旧品的数量α、废旧品残值s、OEM再制造品的单位生产成本cm以及第三方再制造品的单位生产成本ct对OEM和第三方最优利润的影响。 (1) 取ρ=0.8、θ=0.6、α=0.3、cm=0.8、ct=0.5。由命题1,在MPTP、MFTP、MPTF和MFTF 4种情形下,按照s所处的区间s分别设置为0.40、0.30、0.25、0.10。单位授权费f对OEM和第三方最优利润的影响如图1所示。 图1 单位授权费对OEM和第三方最优利润的影响 由图1可知,在MPTP、MFTP、MPTF和MFTF 4种情形下,OEM最优利润均随着单位授权费的增加而增加;第三方最优利润则随着单位授权费的增加而减小。这是由于随着单位授权费的增加,根据推论1第三方由于单位授权费增加进行回收再制造变得越来越无利可图,则逐渐减少回收价格以减少回收量,且利润越来越少;而OEM显然能够通过单位授权费增加获得更多的利润,但随着第三方进行回收再制造越来越无利可图,OEM通过单位授权费增加使自己获利的优势也越来越小。 (2) 取ρ=0.8、θ=0.6、f=0.2、cm=0.8、ct=0.5。由命题1,在MPTP、MFTP、MPTF和MFTF 4种情形下,按照s所处区间s分别设置为0.40、0.30、0.25、0.10。消费者中环保主义者主动无偿返还废旧品的数量α对OEM和第三方最优利润的影响如图2所示。 图2 返还废旧品的数量对OEM和第三方最优利润的影响 由图2可知,在MPTP、MFTP、MPTF和MFTF 4种情形下,OEM和第三方最优利润均随着消费者中环保主义者主动无偿返还废旧品数量的增加而增加。这是由于随着消费者中环保主义者主动无偿返还废旧品数量的增加,根据推论2可知OEM和第三方废旧品回收价格均会降低,在逆向供应链的回收市场节约了回收成本,从而双方的最优利润均会增加。 (3) 取ρ=0.8、θ=0.6、f=0.2、cm=0.8、ct=0.5,废旧品残值s对OEM和第三方最优利润的影响如图3所示。 由图3可知,在MPTP、MFTP和MPTF 3种情形下,OEM和第三方最优利润均随着废旧品残值的增加而增加;在TFMF情形下,OEM和第三方最优利润不受废旧品残值影响。这是由于随着废旧品残值的增加,根据推论3可知,在MPTP、MFTP和MPTF 3种情形下双方均会通过增加回收价格从回收市场获得更多的废旧品,在满足正向供应链的再制造品需求后,可以获得更多的残值收益,残值收益的增加能够抵消回收成本的增加,从而增加最优利润;在TFMF情形下,OEM和第三方均是完全再制造,无法通过废旧品残值获得收益,双方的逆向供应链废旧品回收市场的回收价格和正向供应链再制造品销售市场的零售价格都与废旧品残值无关,因此双方最优利润不受废旧品残值影响。 图3 废旧品残值对OEM和第三方最优利润的影响 (4) 取ρ=0.8、θ=0.6、α=0.3、f=0.2、ct=0.5。由命题1知在MPTP、MFTP、MPTF和MFTF 4种情形下,按照s所处的区间s分别设置为0.40、0.30、0.25、0.10。OEM再制造品单位生产成本cm对OEM和第三方最优利润的影响如图4所示。 图4 OEM单位再制造成本对两企业最优利润的影响 由图4可知,在MPTP、MFTP、MPTF和MFTF4种情形下,OEM最优利润随着OEM再制造品单位生产成本的增加而减小,而第三方最优利润与OEM再制造品单位生产成本的相关关系不确定。这是由于随着OEM再制造品单位生产成本的增加,根据推论4可知OEM将减少再制造品的生产量,其生产成本增加和产量下降则会导致自身利润下降;而对于第三方虽然会增加再制造品的生产量,但利润不一定都增加,究其原因主要是OEM再制造品单位生产成本对逆向供应链回收市场的影响不如正向供应链销售市场直接,还会受到完全再制造和部分再制造策略的影响,因此第三方最优利润与OEM再制造品单位生产成本的相关关系不确定。 (5) 取ρ=0.8、θ=0.6、α=0.3、f=0.2、cm=0.8。由命题1可知分别设置TPMP、TPMF、TFMP和TFMF 4种情形下的s分别为0.40、0.30、0.25、0.10。第三方再制造品单位生产成本ct对OEM和第三方最优利润的影响如图5所示。 图5 第三方单位再制造成本对两企业最优利润的影响 由图5可知,在MPTP、MFTP、MPTF和MFTF4种情形下,第三方最优利润随着第三方再制造品单位生产成本的增加而减小,而OEM最优利润与第三方再制造品单位生产成本的相关关系不确定,此结果与图4类似,此处不再赘述。 当前废旧品回收再制造已经广泛运用于汽车、机械等行业。废旧品的回收是再制造活动的重要环节,再制造商通常采取一定的激励措施从消费者处回收足够的废旧品以保证再制造生产的顺利进行。本文假设第三方需要向OEM缴纳授权费才能进行回收再制造,OEM和第三方在正向供应链销售市场与逆向供应链回收市场均存在竞争,据此建立了以双方闭环供应链利润最大化为目标带约束条件的古诺博弈模型。通过K-T条件得到最优的再制造品生产量以及废旧品回收价格。最后分别通过解析方法和数值算例分析了单位授权费等重要参数对决策变量和最优利润的影响。 本文构建的模型是基于一定假设条件的,因此还存在一定的局限性。今后可从以下4个方面进行拓展研究:① 在逆向供应链回收市场,考虑OEM和第三方两企业以旧换新等其他竞争手段激励消费者回收;② 在正向供应链回收市场,考虑OEM和第三方两企业服务质量等其他竞争手段吸引消费者购买;③ 考虑新产品和再制造品竞争;④ 考虑其他供应链结构,比如引入零售商等。
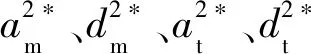
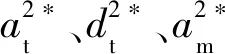
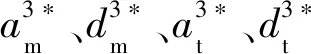
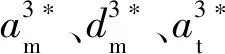
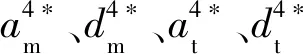
3 灵敏度分析
4 数值算例
5 结 论

