基于概率耦合神经元集群同步活动

丁志远, 焦贤发

(合肥工业大学 数学学院,安徽 合肥 230601)

在神经模型理论研究中,为定量描述神经元集群的同步振荡行为,可以将神经元集群模拟成神经振子集群[1-2]。神经元之间通过突触、间隙等相互连接组成复杂的神经网络,在神经网络中,信息通过突触从一神经元传递到另一神经元。当信号从突触前膜传递到突触后膜时,它的强度主要取决于2个神经元之间峰电位的放电时序。若突触前神经元先于突触后神经元放电,则突触效果增强；反之,突触效果将会得到抑制。近年来,在神经元模型研究中发现突触具有突触可塑性,即在一定条件下信息通过突触之后会造成突触的结构、功能以及数目变化,因此考虑突出可塑造性问题便成为神经动力学研究的热点之一[3]。文献[4-5]基于突触可塑性机制的简化相位模型研究神经元多稳态现象,提出了一种新的突触可塑性演化方程,并用相位差代替突前突后峰电位的相关时间,研究发现在不对称的突触可塑性情况下,多稳态可以存在,即同步、去同步、簇态可以共存。

此外，神经元之间的耦合强度是根据某种规则变化的,耦合神经元同步活动是神经元之间相互作用的结果,文献[6-11]基于带有离散型随机耦合的Hodgkin-Huxley 神经元模型,研究了通道噪声对一个Hodgkin-Huxley神经元的第1个峰值潜伏期的影响,研究发现因为突触间神经递质的随机释放,所以并不是每个突触前的峰电位都会引起突触后反应,进而说明了突触传递信号的方式并非完全可靠,便在文中引入离散型耦合随机变量h:h=1的概率为p(成功引起突触后响应的概率)；h=0的概率为1-p(没有突触后响应的概率)。同时,在现实世界中噪声无处不在,噪声对神经元的放电动力学也具有重要的影响,如文献[12-13]研究了噪声诱导的全局耦合神经元集群的同步现象,研究发现当神经元受到共同的高斯白噪声时,耦合强度阈值会影响到神经振子之间的相互作用以及连结变化,振子之间会产生内部噪声,且噪声的强弱会对耦合强度产生不同的影响。

考虑神经元突触连接之间信息传递的动态随机性,本文在神经元模型中考虑神经元连接耦合强度服从连续型概率分布,据此研究概率耦合以及刺激频率和刺激强度的变化对集群同步活动的影响。

1 数学模型

在外部周期刺激以及噪声共同作用下,N个全局耦合的神经振子集群动力学演化方程为:

Isin(ct)sin(ψi)+ξi(t)

(1)

其中,i=1,2,…,N,N>1；ψi、ψj分别为神经振子i与j的相位;ω为神经振子的自然频率;kj为神经元间的耦合强度;I为刺激强度;c为刺激频率;ξi(t)为随机噪声。

kj的计算公式为:

(2)

其中,ψ0为初始相位；当ψj接近初始相位ψ0时，耦合强度越大；当ψj远离初始相位ψ0时,耦合强度越小。

随机噪声ξi(t)为零均值、δ相关的高斯白噪声，满足：

〈ξi(t)〉=0,〈ξi(t)ξj(t′)〉=2Dδijδ(t-t′),

其中,D为噪声强度。记

Γ(ψi,ψj)=ω+kjsin(ψj-ψi)+

Isin(ct)sin(ψi)

(3)

则将(3)式代入(1)式可得:

相应于(1)式的Fokker-Planck方程为:

(4)

其中,f=f({ψl};t)表示t时刻神经振子相位ψl落入区间(ψl,ψl+dψl)的概率密度,l=1,…,N。

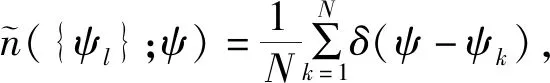
则对平均数密度关于t求偏导得:

(5)

将(4)式代入(5)式,并进行分部积分得:

(6)

当N充分大时,有:

(7)

将(7)式代入(6)式得平均数密度的演化方程为:

(8)

2 数值分析

为研究概率耦合对神经元振子集群活动的影响,本文选取相同的初始条件,分别考虑不同刺激强度和频率引起的振子集群同步程度进行比较,并对(7)式进行数值分析。

神经振子集群放电密度随时间的演化如图1所示。图1中,峰值点表示神经振子同步基于概率耦合机制下活动的强弱,峰值越高同步强度越高。由此可见，神经振子集群同步活动加强。

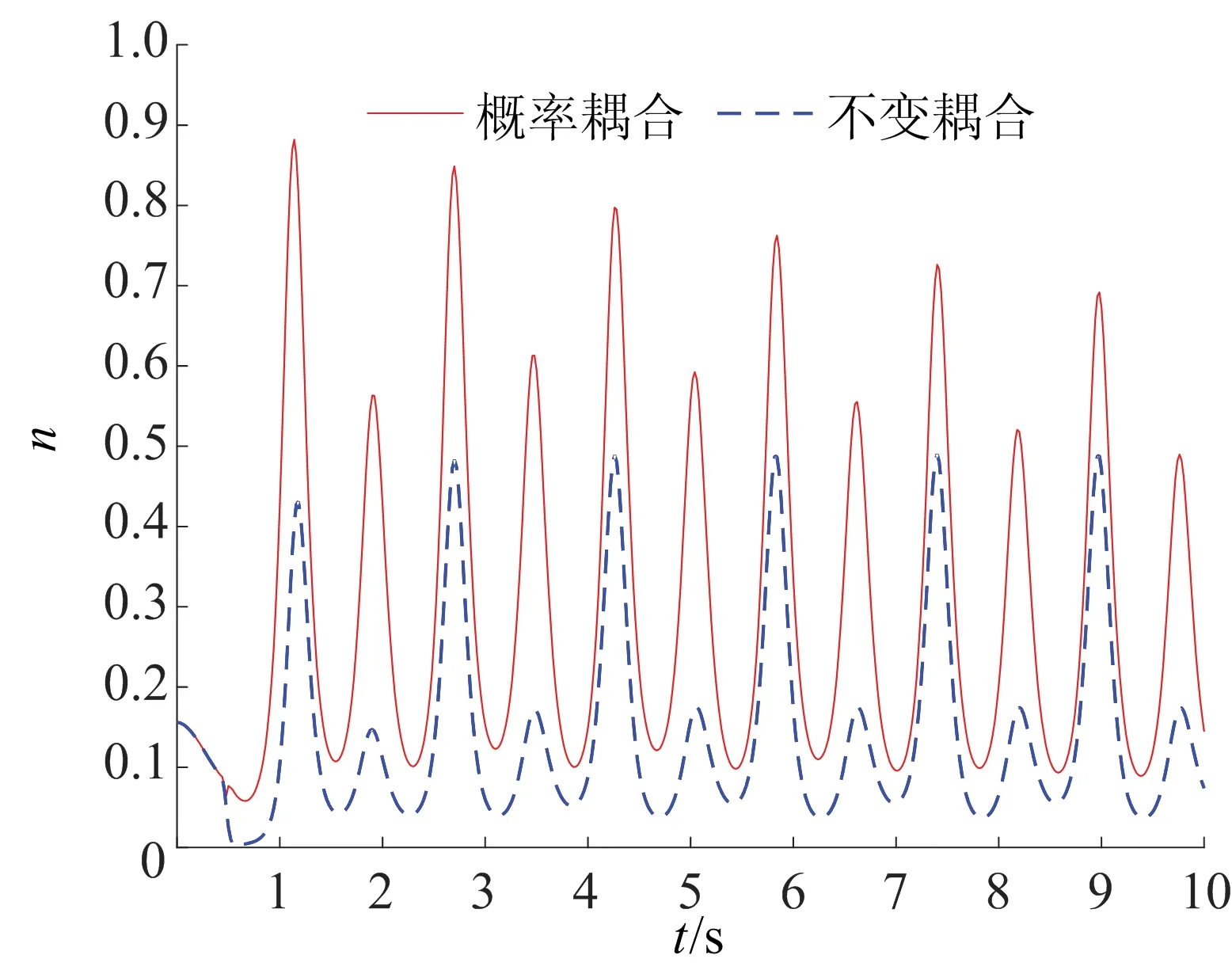
图1 概率耦合情形放电密度随时间的演化

在不同刺激强度条件下,不变耦合神经元集群放电密度随时间的演化如图2所示,概率耦合神经元集群放电密度随时间的演化如图3所示。

图2 不同刺激强度下不变耦合放电密度随时间的演化

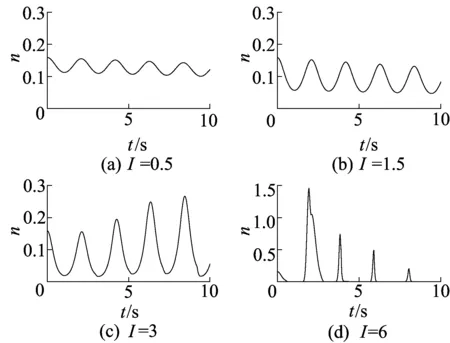
图3 不同刺激强度下概率耦合放电密度随时间的演化

由图2、图3可知,当刺激强度较弱时,2种情形下的神经振子集群的放电呈现周期同步振荡行为;随着刺激强度的增强,不变耦合情形下,神经振子集群周期同步放电会受到抑制变为阵发性放电行为(具体如图2d),概率耦合情形下,神经振子集群的放电呈现周期同步振荡行为,且随着时间推移,同步活动减弱(具体如图3d)。综上可见，在同一刺激强度下,概率耦合作用下神经振子集群放电同步程度明显增强。

在不同刺激频率条件下,不变耦合神经元集群放电密度随时间的演化如图4所示,概率耦合神经元集群放电密度随时间的演化如图5所示。由图4、图5可知,当刺激频率很小时,2种情形下同步放电活动缓慢减弱,随着刺激频率的增强,神经振子集群的同步放电活动随时间推移逐渐消失(具体如图4a、图4b、图5a、图5b);当刺激频率接近神经系统的特征频率时,不变耦合情形下神经振子集群周期同步放电受到抑制变为阵发性放电(具体如图4c、图4d)；概率耦合情形下,神经振子集群先呈现阵发性放电,然后呈现周期同步振荡,并随着时间的推移同步活动增强(具体如图5c、图5d)。

相对于不变耦合的作用,当刺激频率非常小时两者无明显差异；当刺激频率接近神经系统的特征频率时,概率耦合作用下的神经振子集群放电同步行为更为明显。

图4 在不同刺激频率下不变耦合放电密度随时间的演化

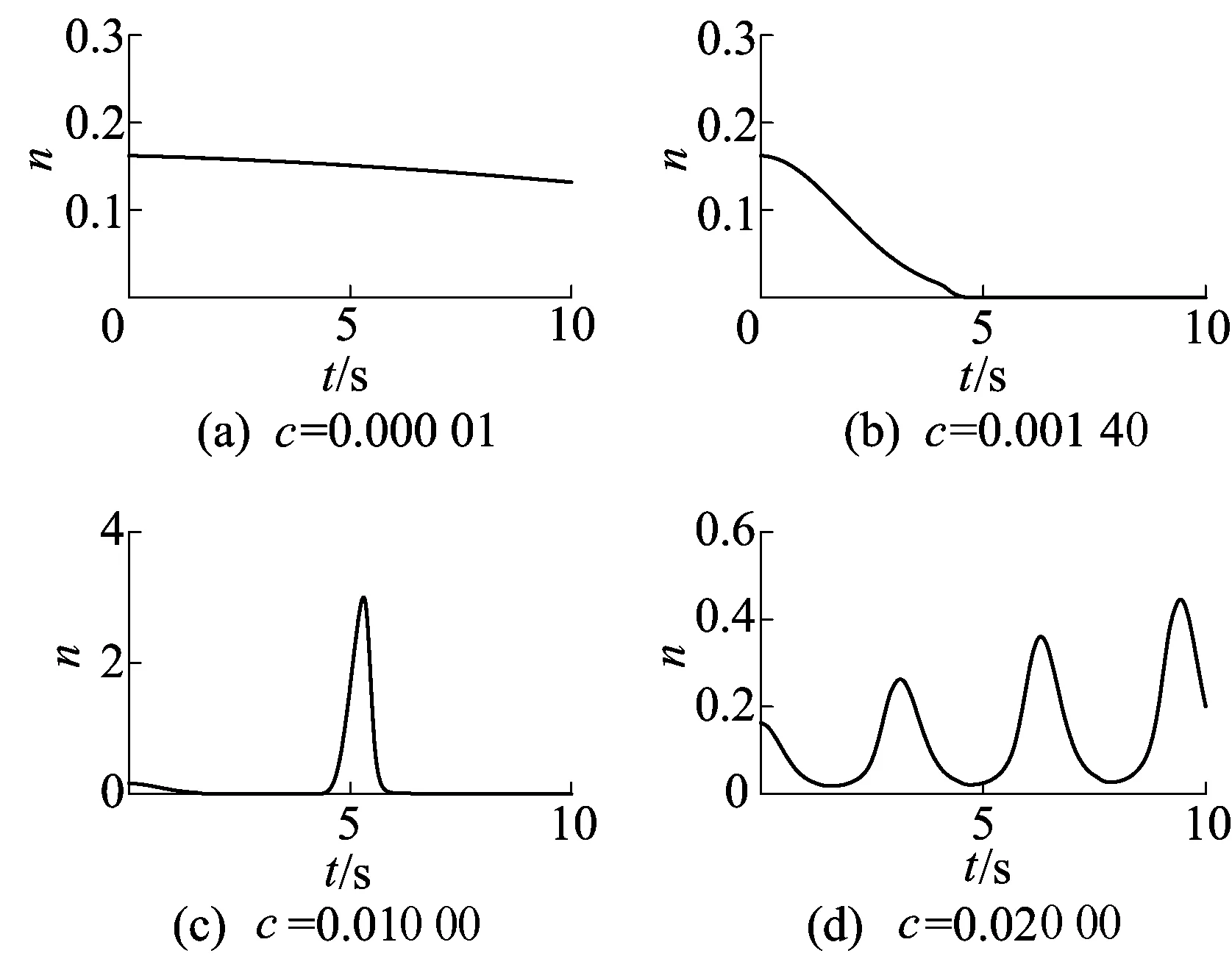
图5 不同刺激频率下概率耦合放电密度随时间的演化

3 结 论

文献[14]研究了耦合神经元模型,揭示了耦合函数的机理及在不同领域的应用。本文在文献[14]基础上,建立了具有外部周期刺激和噪声共同作用下的全局耦合神经振子集群的相位演化模型,并考虑概率耦合情况下对神经元集群同步活动的影响。数值模拟结果表明,在相同噪声强度和刺激强度的环境中,基于概率耦合的同步放电程度相对较高。同时,改变外部刺激强度会影响神经元集群的同步活动,当刺激强度在一定范围内增强,神经元集群呈现周期同步放电活动且也会随之增强,当刺激强度增大到一定值时,神经振子集群的周期同步放电活动会受到抑制。此外,改变外部刺激频率也会影响神经元集群的同步活动,当刺激频率很低时,神经元集群几乎没有出现周期同步放电行为。当系统特征频率接近刺激频率时,神经振子集群的数密度呈现出周期性振荡行为。