基于敏感性分析的悬架多目标优化函数构建方法研究
张 飞, 石 琴, 陈一锴, 彭成旺
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
悬架硬点的空间位置是悬架运动学特性的重要影响因素[1]。在悬架多目标优化问题中,往往通过寻找最佳硬点坐标,以优化汽车的前轮定位参数,从而提高汽车行驶的操纵稳定性[2-4]。前轮定位参数中,主销内倾角和主销后倾角的主要作用是产生回正力矩,以减小转向操纵力;前束角的引入是为了克服外倾角所造成的轮胎偏磨损。因此,基于上述定位参数间的关系,为减少优化目标个数,多采用直接加权法、目标规划法等数理统计方法,分别确定出各定位参数之间的权重系数,从而构建仅有2个优化目标函数的多目标优化模型[4-7]。然而,上述基于数值统计原理的传统方法,仅对各定位参数进行了简单的归一化处理,未考虑前轮定位参数对回正力矩、轮胎磨损的影响,不能准确反映各定位参数间的相对重要程度,难以保证优化结果的科学性与合理性。由于前轮定位参数与轮胎磨损、回正力矩之间存在相关性,即前束角与外倾角的选择对轮胎磨损的影响较大[8];主销内倾角可为汽车提供稳定的回正力矩,而主销后倾角形成的回正力矩随着速度的增加而增大,汽车在不同的车速工况下主销后倾角对回正力矩的贡献率存在较大差异[9]。因此,为合理计算各定位参数间的权重系数,应考虑上述内在关系,以保证优化结果的准确性与有效性。
本文首先采用敏感性分析方法,定量研究主销后倾角、主销内倾角的变化对回正力矩的影响程度,以分别确定高速(100 km/h)、低速(20 km/h)工况下主销后倾角与主销内倾角间的权重系数;基于轮胎磨损对前束角、外倾角变化的敏感性,计算出外倾角与前束角间的权重系数。然后,在高、低速工况下,采用响应面法分别拟合出前轮定位参数与各自静态值(即定位参数的理想设计值)之差的绝对值最大值和悬架硬点坐标的关系模型;基于上述权重系数及关系模型,建立悬架硬点坐标多目标优化模型。最后,采用多目标粒子群优化(multi-objective particle swarm optimization,MOPSO)算法求解上述优化模型,以减少轮胎磨损,提高汽车的操纵稳定性。
1 定位参数与轮胎磨损、回正力矩的关系
1.1 前轮定位参数与轮胎磨损的关系分析
在汽车行驶过程中,当外倾角与前束角匹配合理时,轮胎磨损量达到最小,选取合适的前束角与外倾角极为重要[10]。主销后倾角和主销内倾角对轮胎磨损的影响较小[8],因此本文主要从前束角与外倾角考虑其对轮胎磨损的影响。
轮胎磨损量主要由轮胎与路面间的相互滑移摩擦引起,其值等于耐磨系数与轮胎胎面摩擦功的积[11]。因此,本文采用轮胎胎面摩擦功来表征轮胎磨损量的大小,并构建轮胎胎面摩擦功与前束角、外倾角的关系模型。取轮胎胎面的某一橡胶微块进行分析,如图1所示,则微块的摩擦功为:
E(i,j)=F(i,j)l(i,j)=k(i,j)p(i,j)l(i,j)
(1)
其中,k(i,j)=μA,A为单位面积,μ为静摩擦系数;p(i,j)为橡胶块上的施加载荷的大小;F(i,j)为剪切力的大小;l(i,j)为胎面滑移量。

图1 橡胶微块
将轮胎与地面接触范围内的胎面分成n个微小单元,且假设每个单元在侧向和纵向的变形是独立的,不相互影响。则轮胎的摩擦功为:
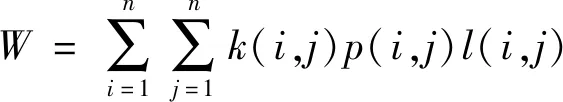
(2)
为防止满载时前轮内倾,加速车轮的偏磨损,安装前轮时应留有一定的外倾角。当轮胎外倾时,会产生一定的侧倾力,引起轮胎表面与地面接触间的侧向滑移,等效为车轮产生一个车轮侧偏角。依据(2)式,对基于刷子模型的轮胎侧偏纵滑工况进行轮胎磨损分析[12],用轮胎胎面摩擦功来表示外倾角与轮胎磨损的关系。摩擦功W[13]为:
W=Wx+Wy
(3)

(4)

(5)
其中,Wx为纵向力所做摩擦功;Wy为侧向力所做摩擦功;a为轮胎接地印迹长的1/2;qz(u)为轮胎载荷分布;ux、uy分别为纵向、侧向车轮附着系数;yt′(u)代表轮胎侧向变形曲线;Sx为纵向滑移率;u为轮胎接地处的坐标变量;uc为轮胎起滑点坐标,其计算式为:
(6)
Δε=(a/3r)α
(7)
其中,μ为车轮总附着系数;η(u)为载荷分布函数;Fz为轮胎垂直载荷;Ktx为胎面分布纵向刚度;Kty为胎面分布侧向刚度;Δε为车轮侧偏角;r为轮胎半径;α为外倾角。
因为车轮存在外倾角,车轮直线行驶时会出现圆锥摆运动,将在地面上出现边滚边滑的现象,从而增加轮胎磨损,所以使用前束角消除前轮外倾带来的这种不良后果[14]。车轮前束角是指车轮中平面与汽车前进方向的纵向垂直平面的夹角,前束角通常偏小,可视为小角度下的车轮侧偏角。因此,摩擦功也可以用来表示前束角与轮胎磨损的关系,摩擦功计算公式为(3)~(5)式。
1.2 前轮定位参数与回正力矩的关系分析
主销后倾角和主销内倾角是形成稳定回正力矩的主要因素。这2个角过小会导致转向的稳定性降低,不利于车辆的自动回正;也不宜过大,否则在转向时导致转向沉重,容易造成驾驶疲劳[14]。因此本文主要考虑主销后倾角和主销内倾角对回正力矩的影响。
车轮转向时,由于离心力的作用,在车轮与路面接触点C处。路面对车轮有一个侧向反作用力Fy,如图2所示。该反作用力使轮胎产生与转向方向相反的的力矩Fye,此力矩除一部分用于克服转向系摩擦力外,剩余部分为回正力矩。主销后倾角γ使转向轮形成回正力矩Mγ的公式[9]为:
(8)
e=rsinγcosθ
(9)
(10)
其中,e为C点至主销轴线的距离;η2为转向系逆传动效率;F1为前轮轴荷;v为速度;L为轴距;R为转弯半径;r为轮胎半径;θ为转向轮偏转角,其表达式为:
θ=arcsin(L/R)
(11)

图2 主销后倾角及其形成回正力矩示意图
汽车转向时,转向轮连同整个汽车前部向上抬起一个相应的高度,使汽车势能增加。当转向外力消失的时候,转向轮偏转过程中积蓄的汽车势能会通过回正力矩形式释放出来,使得车轮恢复到原来的位置。假设转向轮偏转180°,转向轮向上抬起高度h,如图3所示,积蓄的势能使转向轮绕主销轴线形成与转向方向相反的力矩F1h,此力矩除克服转向系摩擦阻力外,剩下的可形成回正力矩。当转向轮偏转角为θ时,主销后倾角β使转向轮形成回正力矩Mβ的公式[9]为:
h=bsin(2β)
(12)
(13)
其中,b为主销转向节偏距。

图3 主销内倾角及其形成回正力矩示意图
2 悬架硬点坐标多目标优化模型
汽车在行驶过程中,前轮定位参数会随行驶工况的变化而出现较大波动,为了提高汽车操纵稳定性和减少轮胎磨损,要求前轮定位参数在行驶过程中尽量保持稳定,使其与静态值的偏差尽量减小。因此,本文优化目标是减小在汽车行驶过程中前轮定位参数与各自静态值之差的绝对值最大值。
根据定位参数间关系的分析,把前轮的定位参数分成主销后倾角与主销内倾角、前束角与外倾角2组。为了使目标函数在高、低速工况下都得到优化,优化目标函数建立如下:
F1h(X)=w1hf1h(X)+w2hf2h(X)
(14)
F1l(X)=w1lf1l(X)+w2lf2l(X)
(15)
F1(X)=0.5F1l(X)+0.5F1h(X)
(16)
F2h(X)=w3hf3h(X)+w4hf4h(X)
(17)
F2l(X)=w3lf3l(X)+w4lf4l(X)
(18)
F2(X)=0.5F2l(X)+0.5F2h(X)
(19)
其中,X=[x1x2x3x4x5x6]T;F1h(X)、F1l(X)分别为高、低速工况下主销后倾角与主销内倾角的关系函数;F2h(X)、F2l(X)分别为高、低速工况下外倾角与前束角的关系函数;wih、wil为高、低速工况下各响应面函数的权重系数;f1l(X)、f2l(X)、f3l(X)、f4l(X)分别为低速工况下主销后倾角、主销内倾角、外倾角、前束角与各自静态值之差绝对值最大值的响应面函数;f1h(X)、f2h(X)、f3h(X)和f4h(X)分别为高速工况下定位参数与各自静态值之差绝对值最大值的响应面函数。
麦弗逊悬架硬点坐标多目标优化模型可以表示为:
minF1(X),minF2(X);
(20)
3 前轮定位参数权重系数的计算
为获取多目标优化函数中各子目标函数的权重系数,本文采用敏感性分析定量研究前轮定位参数对回正力矩、轮胎磨损的影响程度。由主销后倾角、主销内倾角与回正力矩的关系(10)式、(13)式可知,由主销后倾角形成的回正力矩与速度相关,而主销内倾角形成的回正力矩与车速无关,在不同车速下2个角对回正力矩的贡献率不同。因此,分别考虑高、低速2种工况下主销后倾角与主销内倾角间的权重系数。在低速(20 km/h)工况下,根据(10)式、(13)式可计算出当主销后倾角和主销内倾角静态值变化1°时形成的回正力矩变化量,即ΔMγl、ΔMβl;同理,计算出高速(100 km/h)工况下的ΔMγh、ΔMβh。根据(3)~(5)式可计算出外倾角和前束角静态值变化1°时摩擦功的增加量,即ΔWα、ΔWδ。因为摩擦功的计算与速度无关,所以在高、低速工况下外倾角和前束角的ΔWα、ΔWδ不变。低速下主销后倾角、主销内倾角、外倾角、前束角的权重系数w1l、w2l、w3l、w4l计算公式为:
(21)
(22)
(23)
(24)
同理,根据(21)~(24)式可计算出高速工况下前轮定位参数主销后倾角、主销内倾角、外倾角、前束角的权重系数w1h、w2h、w3h、w4h。因此,各个响应面函数的权重系数见表1所列。

表1 各个响应面函数的权重系数
4 整车仿真及目标函数拟合模型
速度是悬架优化模型构建的影响因素,而悬架轮跳试验无法体现速度的影响,因此基于前轮定位参数的关系式,通过整车平顺性试验获取仿真试验数据。响应面法可以有效地揭示设计变量与目标响应之间的关系,并且能够简化后期的优化计算。因此,本文采用响应面法,构建高速(100 km/h)、低速(20 km/h)工况下前轮定位参数与各自静态值之差的绝对值最大值和悬架硬点坐标的响应面模型[15-17]。
4.1 基于ADAMS/Car的整车模型构建
根据安徽江淮某乘用车的设计参数,在ADAMS/Car中建立整车三维仿真模型,如图4所示。模型主要包括前麦弗逊悬架系统、后扭力梁悬架系统、横向稳定杆、转向系统、动力系统、车身和轮胎等。整车部分参数见表2所列。

图4 整车模型

表2 部分整车参数
4.2 前轮定位参数的计算
麦弗逊悬架系统主要部件包括转向节、转向横拉杆、螺旋弹簧、减震器、下摆臂、各部件之间由铰接和衬套连接。前轮定位参数的静态值见表3所列。

表3 前轮定位参数静态值 (°)
麦弗逊悬架系统空间运动简图如图5所示。其中,A、B为下摆臂前、后铰接点;C为下摆臂与转向节铰接点;D为悬架上端与车身铰接点;E为减振器下安装点;G为车轮中心点;H为车轮外端面圆心;K为车轮接地点;N、M为横拉转向杆内、外铰接点;选取的坐标系与车辆坐标系一致。

图5 麦弗逊悬架空间运动简图
根据图5中的几何关系,已知C、D、H、G4个硬点空间坐标,则前轮定位参数的计算公式[18]为:
(25)
其中,γ为主销后倾角;β为主销内倾角;α为外倾角;δ为前束角;xC、yC、zC分别为C点的x、y、z坐标,同理,D点、H点、G点也有对应的x、y、z坐标。
根据(25)式,若已知C、D、H、G坐标随时间变化的曲线,则可计算出前轮定位参数随时间变化的曲线。
4.3 基于响应面法的前轮定位参数拟合模型
根据工程设计经验,选取转向横拉杆外点、转向横拉杆内点、下控制臂外支点、下控制臂前支点、减震器上点等15个硬点坐标用于灵敏度分析[19]。根据灵敏度分析结果,选取对前轮定位参数影响较大的前6个关键硬点坐标为设计变量,即下摆臂外支点x、z坐标,下摆臂前支点z坐标、减振器上点y坐标,转向横拉杆内、外两端点z坐标,分别记作x1、x2、x3、x4、x5、x6。
为拟合得到高、低速工况下,前轮定位参数与各自静态值之差的绝对值最大值和6个设计变量之间的关系模型,分别在车速100 km/h、A级路面(随机路面激励模型)和车速20 km/h、A级路面2种整车平顺性仿真条件下,执行如下步骤:
(1) 以6个设计变量的最大、最小值为2个水平,设计正交试验表。
(2) 选取每一组(一次试验)硬点坐标值,代入整车仿真模型修改其对应的硬点坐标,并在ADAMS/Ride中,对修改后的整车模型进行平顺性仿真实验,得到C、D、H、G4个硬点坐标随路面激励的变化曲线。
(3) 依据(25)式,计算得到前轮定位参数随路面激励的变化曲线,从而计算出每组硬点坐标值的对应响应输出,即前轮定位参数与各自静态值之差的绝对值最大值。
(4) 基于正交试验表的所有数据,采用响应面法,拟合得到响应输出与6个设计变量间的二阶响应面函数[20-21]。
5 麦弗逊悬架硬点坐标多目标优化
5.1 基于粒子群算法的多目标优化
MOPSO算法是将种群中每个个体看成搜索空间中的一个没有体积和质量的粒子,这些粒子在搜索空间中以一定的速度飞行,其速度根据本身的飞行经验和整个种群的飞行经验进行动态调整[22]。MOPSO算法简洁,易于实现,迭代收敛速度快,没有很多参数需要调整,且不需要梯度信息[23-25]。因此,本文采用MOPSO算法进行多目标优化。
5.2 悬架硬点优化结果分析
基于敏感性分析构建悬架多目标优化函数模型,利用MOPSO算法得到新的优化硬点坐标,从而通过整车平顺性试验得到优化坐标对应的高、低速工况下前轮定位参数与其静态值之差的绝对值最大值。
为了分析本文多目标优化模型的效果,将其与用直接加权法建立的多目标优化模型的效果进行对比。直接加权法通过设计指标的变化范围来确定权重系数,当指标的变化范围越大,其权重系数就越小。若采取直接加权法确定车轮定位参数间的权重系数,则前束角、外倾角间的权重系数为0.31、0.69,主销后倾角、主销内倾角间的权重系数为0.67、0.33。构建多目标优化模型,并利用MOPSO算法得到优化硬点坐标,从而得到前轮定位参数与其静态值之差的绝对值最大值。高、低速工况下前轮定位参数与其静态值之差的绝对值最大值(下表中简称为“数值”)的优化结果见表4、表5所列。

表4 低速下前轮定位参数的优化结果 (°)

表5 高速下前轮定位参数的优化结果 (°)
由表4、表5可知,基于敏感性分析的悬架硬点多目标优化,在低速工况下主销后倾角、主销内倾角、外倾角、前束角的优化率分别为15.39%、8.41%、8.20%、25.38%;在高速工况下,定位参数的优化率分别为16.67%、7.40%、8.28%、17.33%;由(14)~(19)式可得,F1(X)的优化率为15.265%,F2(X)的优化率为18.73%。采用直接加权法优化悬架硬点坐标,外倾角的优化率要略高一些,这是因为直接加权法确定的权重中外倾角的权重较大,导致在多目标优化过程中向外倾角偏离;F1(X)的优化率为9.49%,F2(X)优化率为10.41%。总体来说,基于敏感性分析建立的多目标优化模型有更好的优化结果,且在前束角、主销后倾角上有较大的优化率,有利于减小轮胎磨损和提高操纵稳定性,设计更为合理。
6 结 论
为了提高麦弗逊悬架的性能,本文提出了一种基于敏感性分析的多目标优化模型构建方法。将高、低速工况下的8个子目标函数转化成包含2个目标函数的悬架多目标优化模型。运用MOPSO算法进行硬点坐标优化。主要结论如下:
(1) 通过分析前轮定位参数对轮胎磨损、回正力矩的影响,建立了前轮定位参数与回正力矩、轮胎磨损间的数学模型。
(2) 基于敏感性分析方法分别确定高、低速工况下主销后倾角与主销内倾角、外倾角与前束角间的权重系数,发现前束角对轮胎磨损的影响较大以及主销后倾角是影响回正力矩稳定的主要因素。
(3) 优化后的悬架动态性能比优化前有了明显改善且更加合理。优化结果表明,在低速工况下,主销后倾角、主销内倾角、外倾角、前束角的优化率分别为15.39%、8.41%、8.20%、25.38%;在高速工况下,主销后倾角、主销内倾角、外倾角、前束角的优化率分别为16.67%、7.40%、8.28%、17.33%。优化方法有利于减少轮胎磨损和提高车辆的操纵稳定性。

