一种用于矩阵求逆的原位替换算法及硬件实现

张多利, 蒋 雯, 叶紫燕, 宋宇鲲, 汪 健

(1.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601; 2.中国兵器工业集团 第214研究所,安徽 蚌埠 233000)

0 引 言

随着数字信号处理技术的发展,矩阵求逆[1]运算的应用领域日益广泛。人工智能技术[2]、图形图像处理、雷达技术以及实时通信技术等都涉及了大量的矩阵求逆运算[3],而这些工程领域都有高吞吐量、实时性运算要求,如何利用有效资源实现快速大规模矩阵求逆运算成为了硬件设计的重点和难点。

传统的矩阵求逆方法,如初等变换法、伴随矩阵法、Gauss-Jordan消去法[4]等,由于其固有的数学属性而不适于硬件实现，工程上常用的矩阵求逆方法有Cholesky分解求逆法[5]和QR分解求逆法[6-7]。Cholesky分解求逆法计算量不大,但其是对对称正定矩阵进行三角分解,适用矩阵范围太小。QR分解求逆法运算量较大,中间有大量数据相关的迭代过程,还涉及大量开方和范数运算,运算时间较长,并行度不高,资源消耗量太大。

为了平衡计算效率和资源消耗,本文利用基于LU分解的按位替换算法[8]对矩阵进行求逆。该算法运算算式相对简单,不需要大量的开方、求范数等复杂运算;且该算法与利用LU分解[9]进行矩阵求逆的常规算法相比,可以直接并行求三角逆矩阵,具有优越的可并行性,降低了运算时间复杂度。基于该算法的硬件架构在源数据存储空间上进行求逆运算和结果存储,无需占用额外存储资源,实现了运算资源和存储资源的复用,具有优越的可应用性。

1 算法分析

设所有顺序主子式不为0的M阶方阵矩阵A为:

其中,aij为第i行第j列元素(i,j=1,2,3,…,M)。采用按位替换法进行矩阵求逆,需要先对待求逆矩阵A进行约化系数求解,得到M阶约化系数方阵N。N的第1行和第1列元素为:

(1)

其中,i,j=1,2,3,…,M。N的其他元素为:

(2)

其中,i=2,3,…,M;j=i+1,i+2,…,M。最后得到约化系数矩阵N,即

由N可直接并行求得待求逆矩阵A分解所得的下三角阵L的逆矩阵L-1和上三角矩阵R的逆矩阵R-1。由L-1左乘R-1可得到矩阵A的逆矩阵,即A-1=R-1L-1。

L-1的元素lii为:

(3)

其中,i=1,2,3,…,M。L-1的元素lji为:

(4)

其中,i=1,2,3,…,M-1;j=i+1,i+2,…,M。则L-1为:

R-1的元素rii为:

(5)

其中,i=1,2,3,…,M。R-1的元素rji为:

(6)

其中,j=1,2,3,…,M-1;i=j+1,j+2,…,M。则R-1为:

按原位替换算法进行矩阵求逆的算法原理与传统矩阵求逆算法相比,避免了传统算法中大量的开方、平方、求范数等复杂运算;通过创建约化系数矩阵,沿对角线对称的上三角矩阵元素和下三角矩阵元素可以并行计算,避免了传统算法中大量的串行迭代过程,运算时间得到压缩,并行度有所提高;采用按位替换的方式,在硬件设计中所有数据都存在原存储空间中,减少了存储资源消耗。

2 地址无冲突设计

基于原位替换的矩阵求逆算法,即整个运算过程的数据更替都在原矩阵所占的存储空间内进行。由于整个运算过程都是采用高效并行计算,矩阵源数据、中间数据和结果数据的读取顺序和存储方式直接决定着整个设计的运算高效性、正确性及数据读取的安全性。因此,读取顺序和存储方式的设计以及无冲突地址的生成是整个矩阵求逆设计的重中之重。

本文先进行约化系数矩阵计算,再对矩阵进行数据预处理和三角逆矩阵计算,最后是上、下三角逆矩阵乘运算。其中数据的预处理过程为接下来的三角逆矩阵运算作了简化,避免了三角逆过程中由于数据存取方式变化带来的地址读写冲突。运算所需存储器中,有1组块存储器Memory0由8小块1 024×64 bit的片上随机存取存储器(random access memory,RAM)组成;另3组存储器dist-mem0、dist-mem1和dist-mem2均由8小块16×64 bit小的分布式RAM组成。运算数据采用32位浮点数形式,如此,对于1个小块存储器来说,读取1个地址可以得到2个数据;对1个大块存储器来说,读取1个地址可以得到16个数据。这样在整个运算过程中,多组源数据可从2组存储器中并行读取,避免了由于高并行度紧凑计算带来的数据冒险。

2.1 存储资源管理分配与约化系数矩阵计算

在源数据存储模式下,将上、下三角元素沿对角线“对折”,第i行第j列元素和第j行第i列元素两两拼接,分别作为高32位和低32位,放在1个存储地址空间内,每读1个地址,能输出2个元素,避免了地址冲突。其中对角元素存入dist-mem0,非对角元素存入Memory0。

对于前M/2行(列)非对角元素,每8行(列)为1个循环,每行(列)的第1个元素按规律存入memx的某一地址,同行(列)的前8-x个元素按顺序存入memx至mem7的同一地址,剩余元素每8个按顺序存入mem0至mem7的同一地址,其中memx为Memory0的组内存储器号。

对于后M/2行(列)非对角元素,每8行(列)为1个循环,每行(列)的第1个元素按顺序存入memx至mem7的同一地址,同1行(列)的前8-x个元素按规律存入memx的某一地址,剩余元素每8个按顺序存入mem0至mem7的某一地址。对于对角元素,每8行(列)为1个循环,顺次存储在dist-mem0中。

以8阶矩阵求逆存储方式为例,8阶矩阵非对角元素无冲突存储方式见表1所列,矩阵对角元素无冲突存储方式见表2所列。

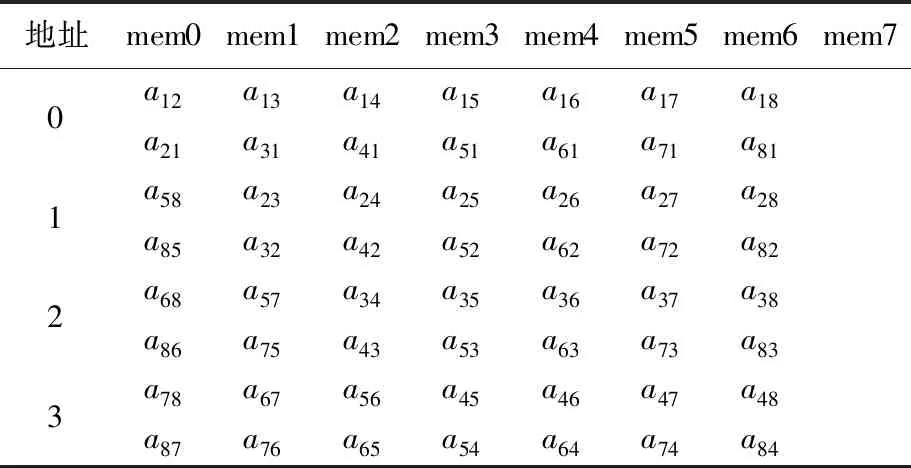
表1 8阶矩阵非对角元素无冲突数据存储方式

表2 8阶矩阵对角元素无冲突数据存储方式

约化系数计算模式下数据存取步骤如下:

(1) Memory0输出当前行需要循环取的数据,存入dist-mem1。

(2) Memory0和dist-mem1分别提供约化系数计算单元(processing element,PE)PE1中乘法器的2组源数据。

(3) dist-mem0向PE1中的除法器提供源数据。

(4) Memory0提供减法器所需要的1组源数据。

(5) 将非对角元素结果回写至Memory0中,仍保持上、下三角元素合为1个地址的存储方式,其数据地址与源数据地址一致。

(6) 在约化系数对角元素结果计算结束后,由三角逆矩阵对角元素计算单元PE2随后计算出逆矩阵的对角元素,并存入dist-mem2中。

以4阶矩阵进行矩阵求逆为例,数据搬运原理如图1所示。

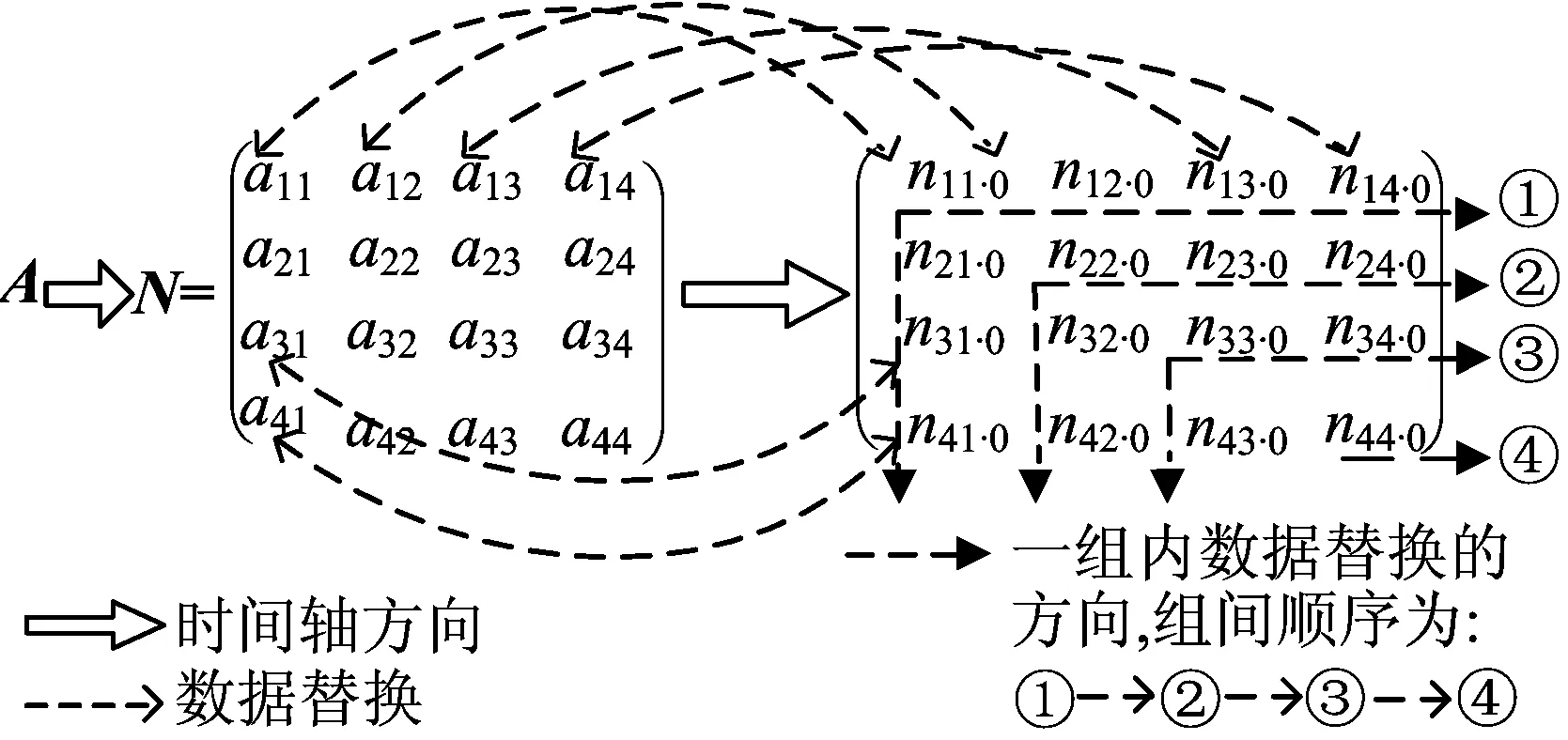
图1 约化系数矩阵数据搬运原理示意图

图1中,采用原位替换的矩阵求逆算法,约化系数矩阵沿对角线对称的上三角矩阵元素和下三角矩阵元素可以并行计算;未用箭头标出的元素与已标出元素执行相同的操作。

2.2 预处理和三角逆矩阵计算

在求得约化系数矩阵后对数据进行2步预处理,避免了由于地址读写复杂带来的冲突,为求上、下三角逆矩阵作了简化。在数据预处理计算模式下的数据存取步骤如下:

(1) Memory0提供乘法器所需的一组数据njk·(k-1)或nki·(k-1),dist-mem2提供乘法器所需要的另一组数据lkk或rkk,并将结果回写至Memory0中,其数据地址与源数据地址一致。

(2) Memory0提供乘法器所需的一组数据njk·(k-1)·lkk或者nki·(k-1)·rkk,dist-mem2提供乘法器所需的另一组数据ljj或rii,并将结果回写至Memory0中,其数据地址与源数据地址一致。

在上、下三角逆矩阵计算模式下,Memory0提供上、下三角逆矩阵计算单元PE3中乘法器的2组源数据,并作为三角逆矩阵结果存储模块,在相应周期后将数据回写至Memory0,期间为保证数据存取有效,将中间结果缓存至dist-mem0。三角逆矩阵数据搬运原理如图2所示。图2中,矩阵中每条虚线上的元素运算时间相同,运算顺序为先计算靠近对角元的虚线,再沿着2个顶点逐渐向外扩散进行运算;未用箭头标出的元素与已标出元素执行相同的操作。

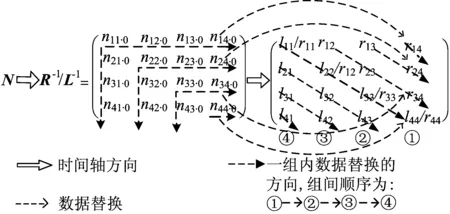
图2 三角逆矩阵数据搬运原理示意图

2.3 上、下三角逆矩阵乘运算

在矩阵乘计算模式下,采用直接矩阵乘的方式,Memory0组内的8组mem采用一端读数一端写数的模式,设置2组乘加PE,每8个乘加器为1组PE,循环取数并行完成第i行(列)的数据运算。在整个矩阵乘运算过程中,除当前行自相乘得到对角元素数据外,其余各行交叉提供源数据,得到非对角元素结果。

以前2行(列)为例,在计算第1行(列)时,随着列计数的递增,上三角逆矩阵第1行元素先依次和下三角逆矩阵第1列元素相乘,再依次和第2列、第3列……元素相乘。

当行计数与列计数相等时,首先利用第1组矩阵乘运算PE得到对角线元素。

当列计数大于行计数时,上三角逆矩阵第1行元素利用第1组PE依次和下三角逆矩阵第2列、第3列……元素相乘,上三角逆矩阵第2行、第3行……利用第2组PE与下三角逆矩阵第1列相乘,2组PE共同作用完成结果矩阵第1行和第1列的逆矩阵结果输出。

在计算第2行(列)时,同样首先上三角逆矩阵第2行元素利用第1组PE和下三角逆矩阵第2列元素相乘,之后第3行、第4行……元素利用第2组PE与第2列元素相乘,2组PE共同作用完成结果矩阵第2行和第2列的结果输出。

此后的每行(列)依照上述相同规律相乘直到完成整个逆矩阵的结果输出。

求4阶三角逆矩阵的矩阵乘结果数据搬运流程如图3所示。图3中沿着对角线对称的上三角逆矩阵元素和下三角逆矩阵元素对称存储在Memory0的相同地址空间,结果元素回写至Memory0中;未用箭头标出的元素与已标出元素执行相同的操作。

各PE内部互连结构如图4所示。图4中,M0in表示存入Memory0的数据;D1in表示存入dist-mem1的数据;D0in表示存入dist-mem0的数据;MUX表示运算中的符号判断;reg=1表示寄存器数据为1;Rout0表示求得的三角逆矩阵对角元素;Rout1、Rout2表示求得的三角逆矩阵非对角元素。

约化系数和预处理运算模式下,PE内各运算器互连结构示意图如图5所示。共2组PE,每组PE内各8路PE1,并行完成约化系数矩阵的上、下三角元素计算,PE2则计算完成三角逆矩阵的对角元素数据。图5中,Control-1表示约化系数运算和预处理控制端;MUL-Group表示乘法运算块;PE1-Group表示约化系数运算块;Mem表示各存储块。

三角逆矩阵运算模式下,PE内各运算器互连结构示意图如图6所示。共2组PE,每组PE内各8路PE3,并行完成上、下三角逆矩阵计算。图6中,Control-2表示上、下三角逆矩阵计算控制端;PE3-Group表示上、下三角逆矩阵元素运算块。

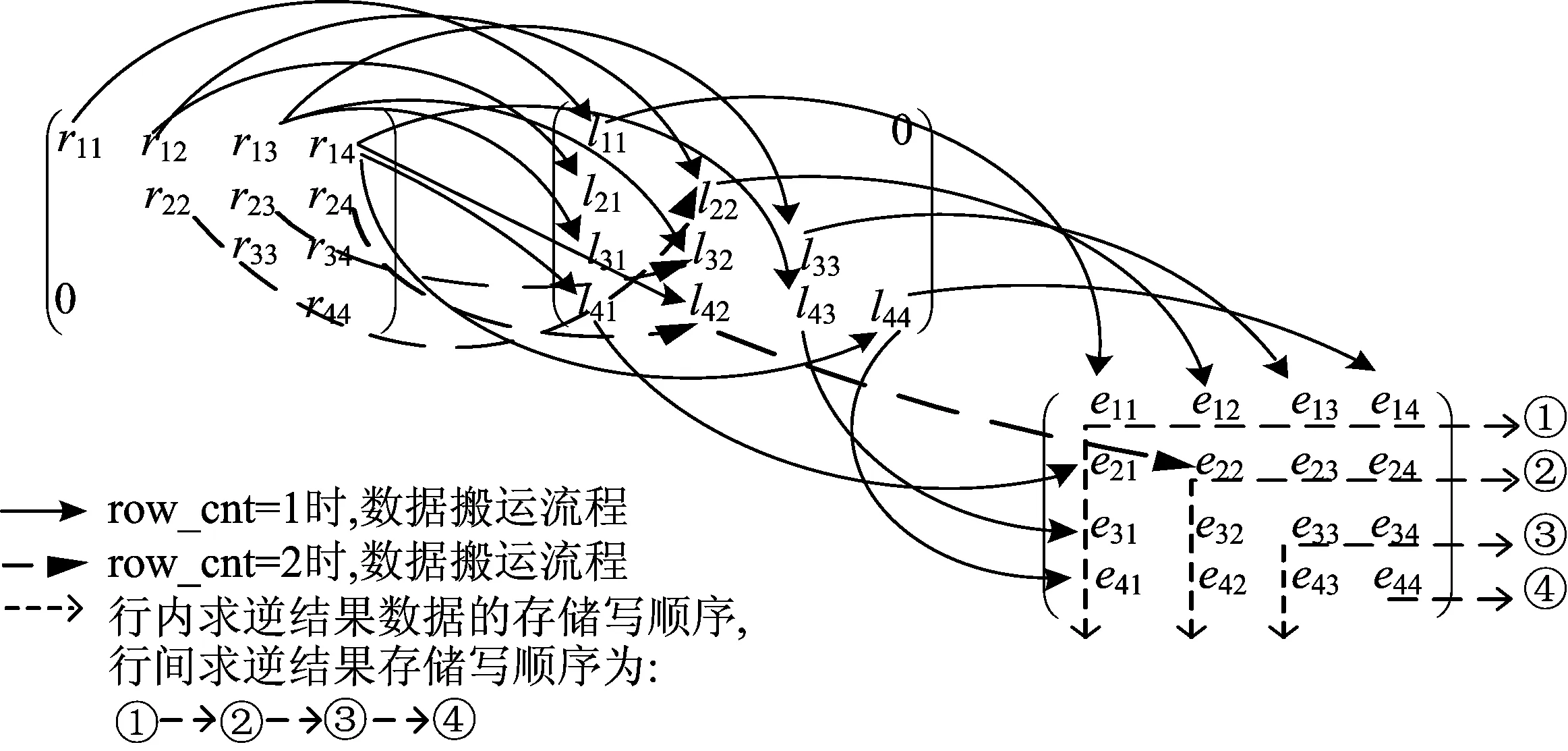
图3 对三角逆矩阵进行矩阵乘的数据搬运流程

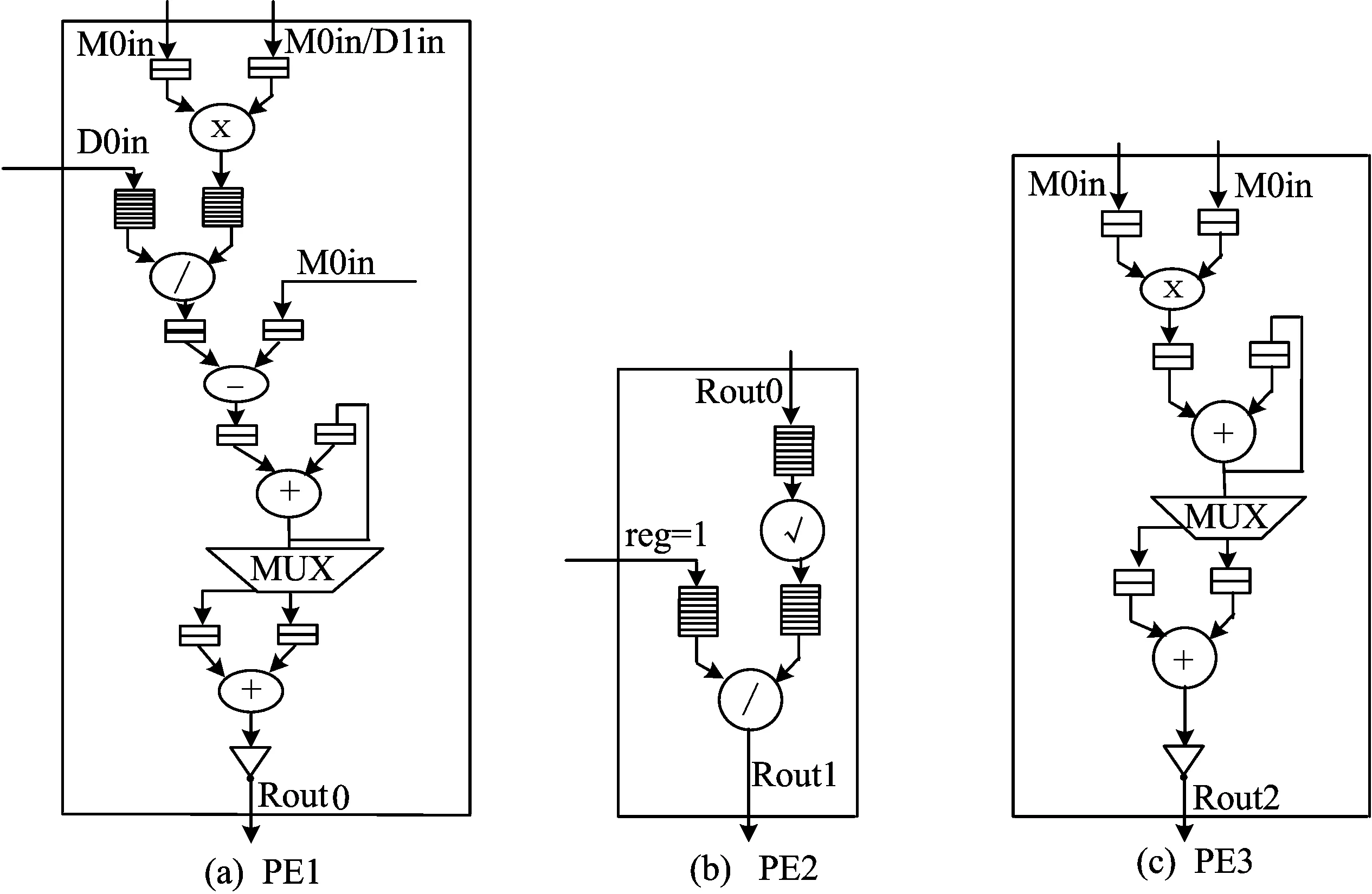
图4 各PE内部互连结构

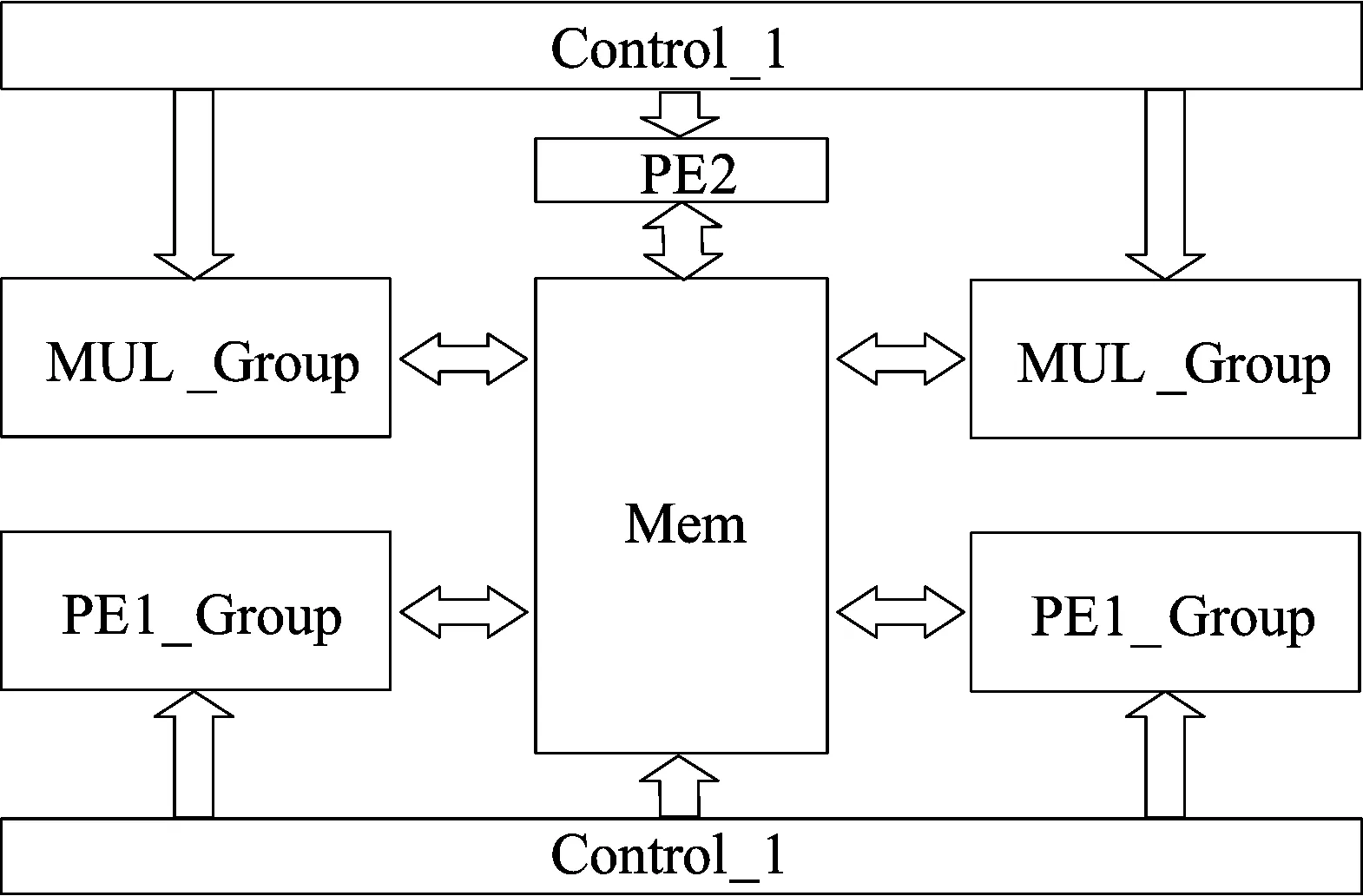
图5 2×8路约化系数运算和预处理互连结构

图62×8路三角逆矩阵运算互连结构

3 实现与对比

本文利用Matlab选取矩阵元素在[-1,1]和[-100,100]2种取值范围内,各阶顺序主子式不为0的2n矩阵作为测试源矩阵,基于存储空间的选取大小,验证完成24(16)阶、25(32)阶、26(64)阶和27(128)阶这4种规模的矩阵求逆。

各阶数矩阵在不同源数据范围内的求逆硬件测试结果和Matlab仿真结果对比,误差见表3所列。

由表3可知,本文采用原位替换算法进行矩阵求逆与Matlab仿真实验结果相比,硬件电路求逆的结果精度能达到10-6,具有良好的运算性能。经测试所设计的硬件架构综合频率在120 MHz以上,能够满足高速运算的要求。

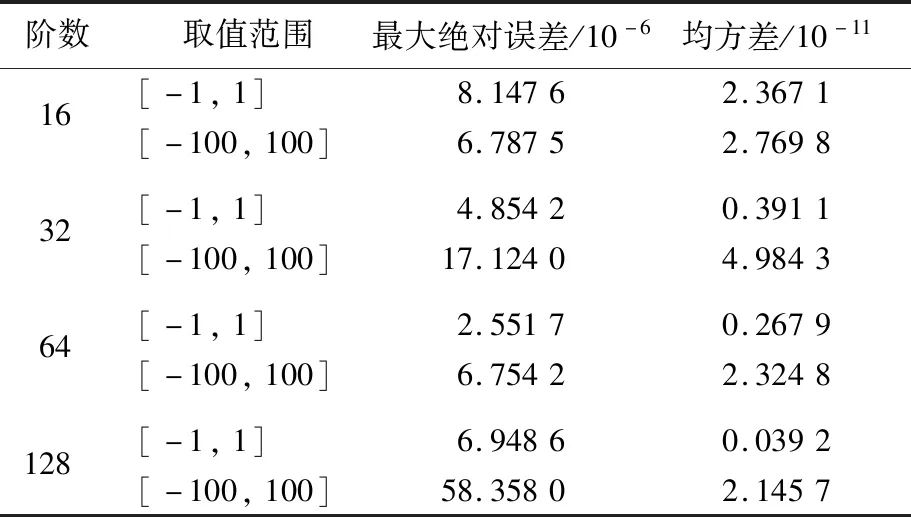
表3 矩阵求逆误差

所设计的硬件架构完成矩阵求逆运算的理论计算时间与实际计算时间对比见表4所列。

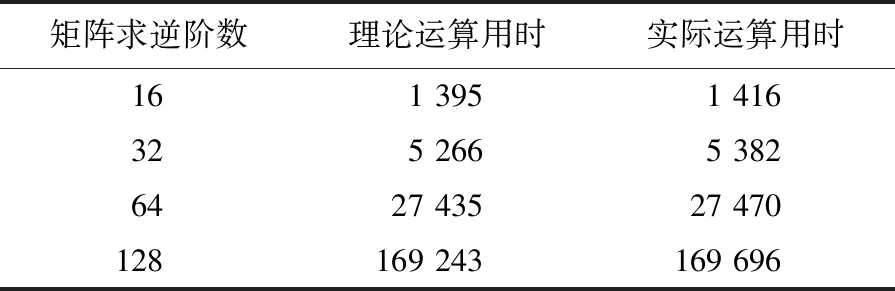
表4 完成求逆所用时间与理论时间

注：运算用时数据为周期数。

与文献[10]相对比,本文设计用时更短,32阶矩阵求逆能达到近10倍的加速比;与采用常规LU分解[11]和QR分解进行矩阵求逆的硬件设计相比,本文设计采用按位替换法,通过创建约化系数矩阵,分解了串行迭代的过程,提高了算法的可并行度。采用原位替换和LU分解进行矩阵求逆的硬件加速比见表5所列。

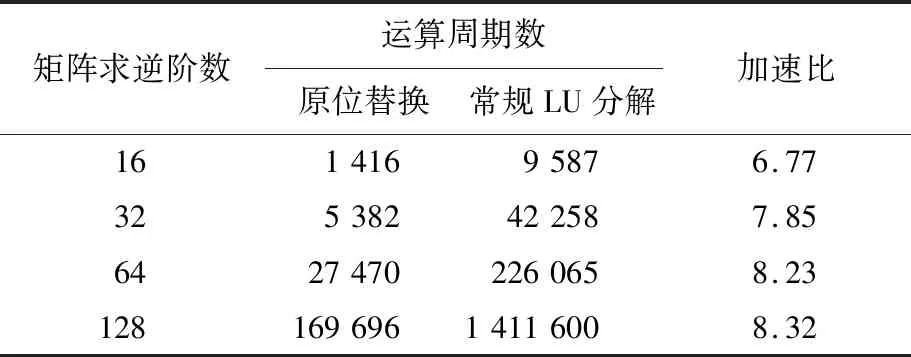
表5 矩阵求逆硬件运算加速比

原位替换法进行矩阵求逆的整个计算过程中,各个模块都根据相应的对称轴进行并行运算,各个模块结果均储存在原存储空间,不占用额外资源,有效地压缩了资源消耗。由于各模块分步有序进行,不会产生由于数据运算不完全带来的拖尾效应,极大地保证了结果的正确性和数据的安全性。原位替换法实现了运算过程间分步有序,同一运算过程内上、下三角并行,同一三角内PE并行的“三维运算”。

4 结 论

本文分析了面向复杂信号处理和高密度计算的算法类型特点,根据按位替换法进行矩阵求逆的算法原理,设计实现了一款能够完成2n阶矩阵求逆运算的硬件架构,并且提出了一种针对算法的地址无冲突设计,在保证多维、高并行度计算的情况下,平衡了存储接口、数据安全、资源消耗及运算速度的问题。