面向多舵机串联驱动的机器鱼游动行为研究

陈 奇, 姚志刚, 吴 寅, 田文锋

(合肥工业大学 机械工程学院,安徽 合肥 230009)

0 引 言

按照推进部位的不同,鱼类的游动方式可分为身体/尾鳍 (body/caudal fin, BCF) 游动模式、中间鳍/对鳍(median/paired fin,MPF) 推动模式两大类[1]。根据文献[2],85%的鱼类采用BCF游动模式。BCF游动模式由躯干伸缩波动和尾鳍摆动形成推力,具有游动速度快、效率高、加速性能强的特点,因此适合在游动任务时间长、游动距离远、游动速度或加速度要求高的场合。

近年来,由于BCF游动模式的机器鱼具备推进效率高且速度快的特点,很多学者对BCF游动模式进行了研究,取得了一系列成果。在BCF游动模式分类上,文献[1]最早将BCF分为鳗鲡模式、鲹科模式和箱鲀科模式；随后,文献[3]又分别在BCF游动模式的分类基础上增加了亚鲹科模式和鲔科模式，并对游动模式的波动、摆动属性进行了总结分析。在BCF鱼类的推进方式上,文献[4-5]根据小振幅位移理论,推导出适用于鲹科和鳗鲡鱼类的细长体理论,并由此建立了鲹科鱼类推进模式的数学模型;文献[6-7]定义了由鱼体波动所产生的尾涡,并基于此提出了著名的“二维波动板理论”;此后,文献[8-9]设想鱼类身体波和外形参数会对鱼体推进性能产生影响,以扩展和改进二维波动板理论,由此建立了“三维波动板理论”;文献[10]、文献[11]分别基于二维、三维N-S方程(Navier-Stokes equations),利用计算流体力学(computational fluid dynamics, CFD)方法进行了鳗鲡鱼类的推进模式分析;文献[12]从揭示鱼类外形仿生和运动仿生中蕴含的仿生机理出发,提出了一种机器鱼自主游动中的流体结构耦合新方法,将流体变量和结构变量同步进行推进。由于上述理论的复杂性及效率较低的因素,为实现机器鱼快速高效的推力和效率估算,文献[13]基于理想推进器理论进行了两自由度尾鳍推进机制研究,验证了基于理想推进器理论的正确与有效性。

由以上分析可知,当前机器鱼在鱼类推进理论上已有较多研究,并建立了相关影响机理模型,而细化到BCF推进模式上,尤其是基于舵机驱动的BCF游动模式仿生机器鱼,有关其结构及运动参数对机器鱼游动影响机理的研究还较少,且当前在机器鱼推进模式的研究上,多数仅考虑尾鳍推力,而忽略了鱼身波动的影响。

本文拟对舵机驱动的机器鱼开展基于多舵机串联驱动的机器鱼游动行为规律及其影响因素的研究。首先建立其运动学仿真模型,然后对舵机设定不同驱动参数,利用虚拟样机技术实现各种驱动方案包络线求解,依据理想推进器理论,进行机器鱼尾鳍与鱼身动力特性的数值模拟,获得各种驱动方式机器鱼动力学结果,并对尾鳍动力特性模型数值进行修改,最终得出基于多舵机串联驱动的机器鱼鱼体运动参数对鱼体运动特性的影响关系。以此来揭示基于舵机驱动的机器鱼游动机理,为由舵机驱动的机器鱼设计、制造及动力学估算提供依据与指导。

1 多舵机驱动机器鱼模型建立

1.1 机器鱼工作原理

鱼体的推进行波可简化为一个由鱼头向鱼尾方向传播且波动幅度逐渐增加的正弦曲线,因此鱼体推进行波可利用波幅包络曲线与正弦曲线合成得出。

文献[4]利用简单的二次样条曲线来拟合身体波波幅包络曲线,其数学描述为:

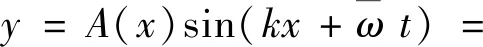
(c1x+c2x2)sin(kx+ωt)

(1)

其中,c1、c2为鱼体包络线的一次和二次增益,其取值与鱼体尺寸及其游动模式相关;x为沿鱼体方向的位移量;A(x)=c1x+c2x2为波幅包络线;k=2π/λ=2πR/L,λ为鱼体波波长,R为波数,L为鱼体长度;角速度ω=2πf,f为鱼体波频率。

根据文献[14],c1可取0.4,c2可取0.6,λ可取1.0,将运动周期T内的时间t离散化,由给定的已知参数作出鱼体波幅包络线示意图如图1所示。

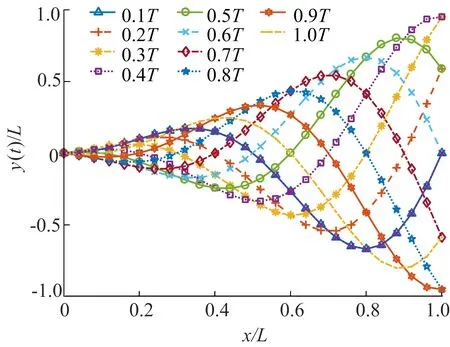
图1 鱼体波幅包络线示意图

1.2 机器鱼驱动方案设定及模型建立

为模拟鱼类游动所形成的波幅包络线,结合数字舵机(digital servo)的高精度、大频宽、响应迅速、适应范围大等特点,以多舵机串联为驱动方案,利用控制模块、密封模块、驱动模块及连接模块等实现机器鱼的游动模拟。

基于多舵机串联驱动的机器鱼总体结构如图2所示。

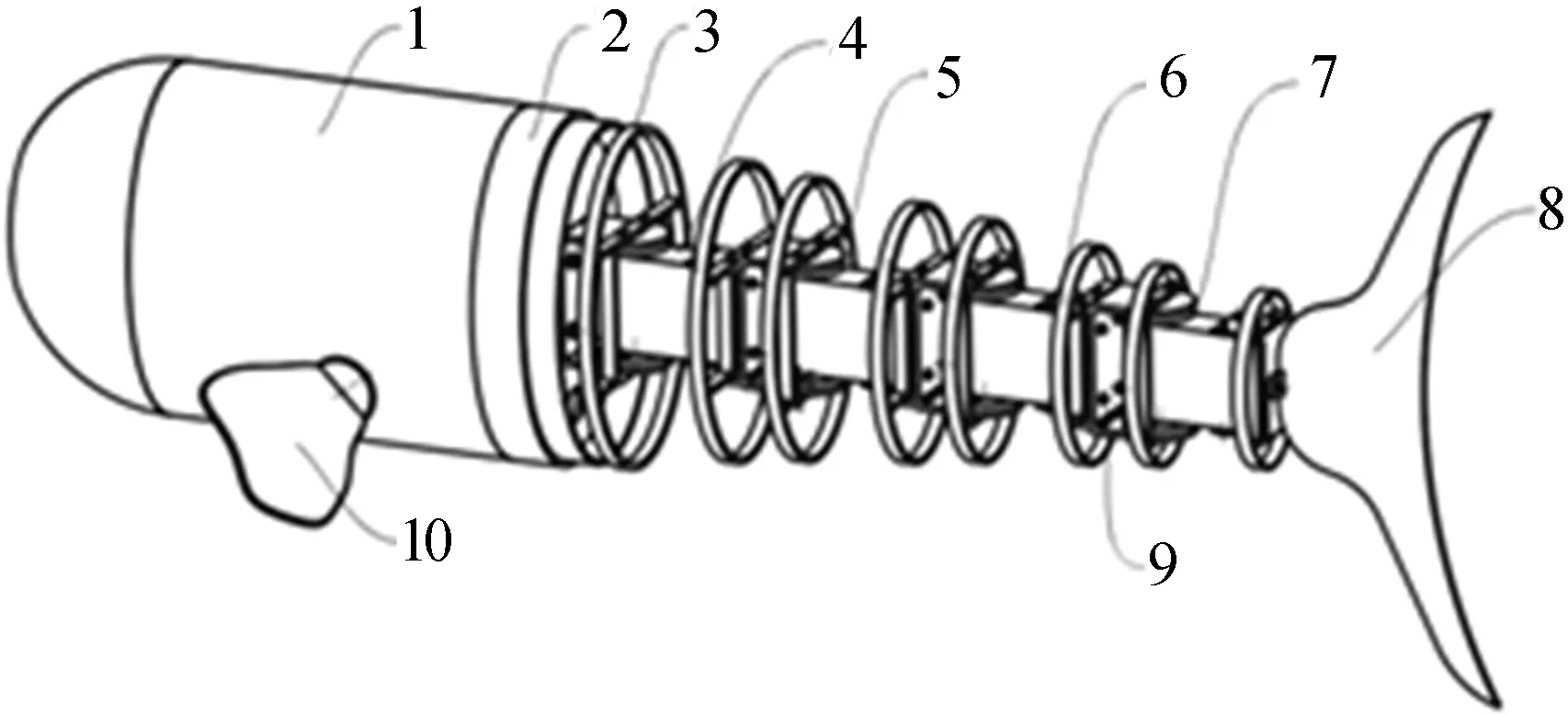
1.壳体 2.连接件 3.支撑环架 4.舵机 5.大固定连接块6.小固定连接块 7.舵盘 8.尾鳍 9.螺钉 10.胸鳍

2 多舵机驱动机器鱼动力学仿真

2.1 机器鱼行波运动仿真

针对多舵机驱动机器鱼,以舵机驱动数量及是否与前一个舵机具有相位差为分类依据,去除无舵机驱动这一特殊情况,共有15种舵机驱动方案,见表1所列,其中以图2中靠近鱼头的舵机作为舵机1,从鱼头沿鱼尾方向依次为舵机2、舵机3及舵机4。

本文基于此15种舵机驱动方案,利用ADAMS仿真模拟出机器鱼运动图谱如图3所示。

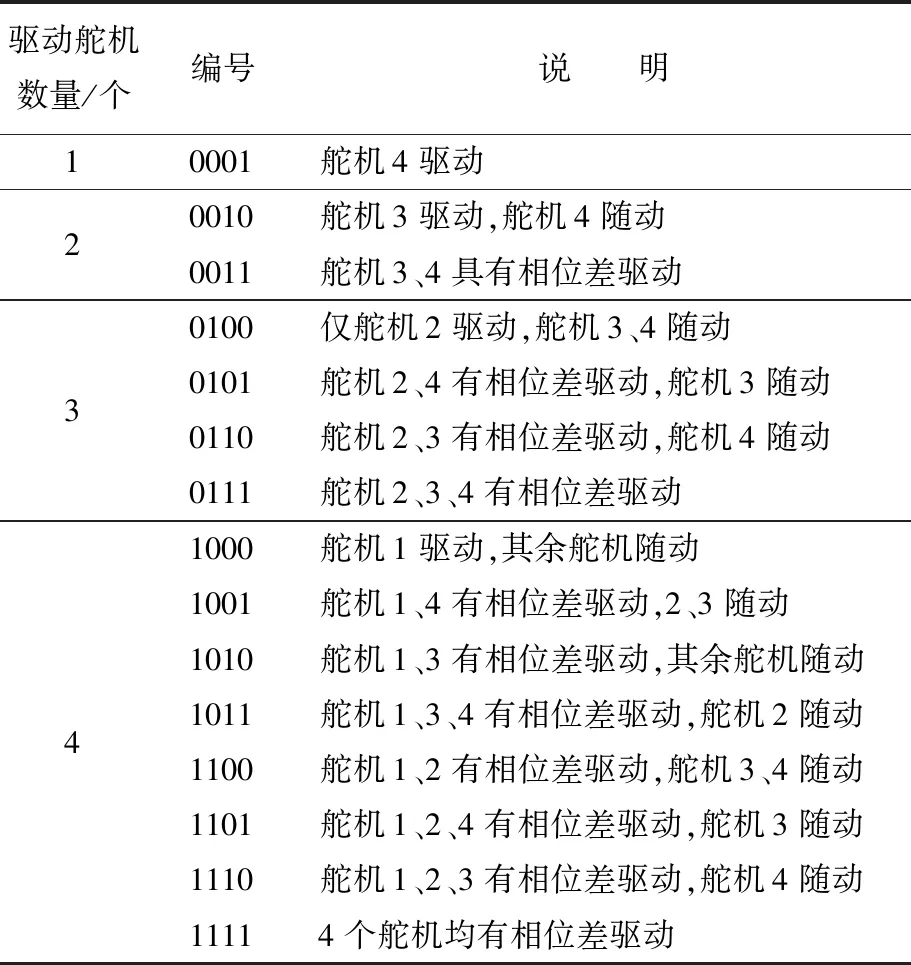
表1 机器鱼舵机驱动方案

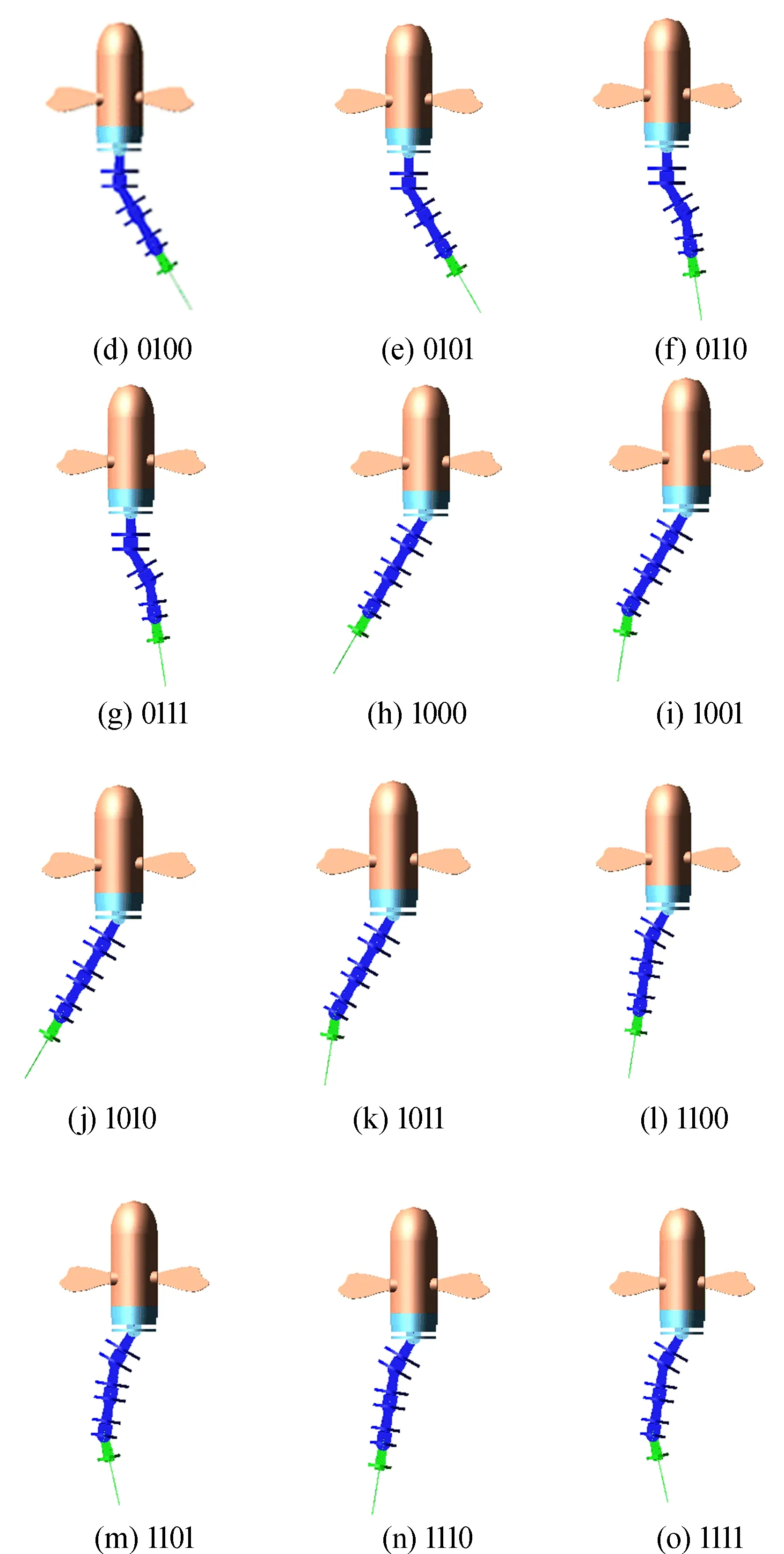
图3 不同舵机驱动方式机器鱼运动图谱

2.2 机器鱼波幅包络线形成

如图3所示,在机器鱼不同驱动方式的游动过程中,选取舵机1、舵机2、舵机3、舵机4这4个特殊位置的位移进行数据分析,得到舵机位移之间的关系,导出ADAMS数据,作出机器鱼游动时波幅包络线,如图4所示(鉴于篇幅所限,本文仅给出3种驱动方式的波幅包络线)。

根据图4中基于舵机的不同驱动方式所形成的包络线,可知当舵机数量增多且前、后舵机具有相位差时,所形成的鱼体包络线更加符合机器鱼S型游动曲线。

本文将图4c中的第15种驱动方案所形成的包络线利用Matlab工具中的样条曲线拟合,即考虑鱼身的弯曲程度影响,得到4个舵机之间具有相位差的摆动所形成的包络线，具体如图5所示。

从图5可以看出,本文设计的基于舵机驱动的机器鱼在水下游动时,4个舵机利用均匀相位差同时协调工作,可达到 S型BCF推动效果,整体鱼身的游动范围在包络线之内,符合文献[3]利用简单二次样条曲线来拟合身体波波幅的包络曲线。

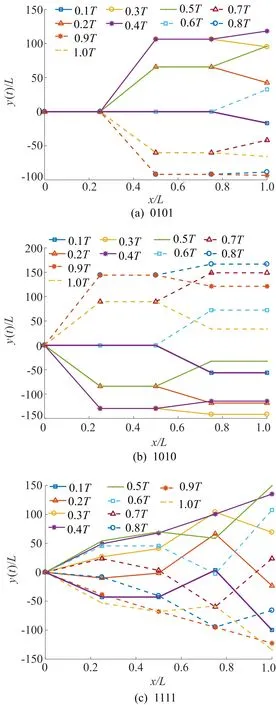
图4 3种驱动方式的波幅包络线

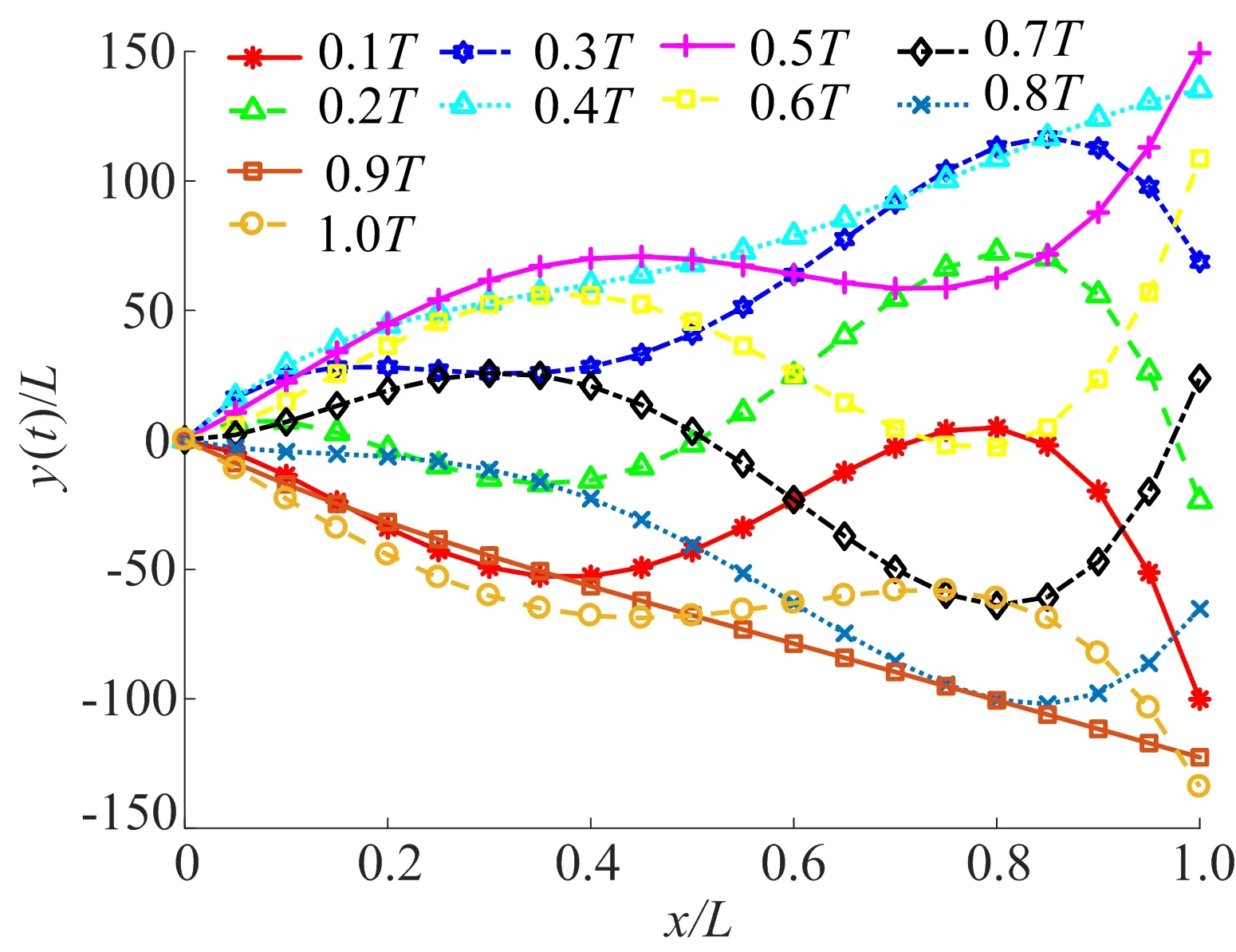
图5 拟合后的机器鱼游动包络线

3 机器鱼游动行为研究

3.1 机器鱼理想推进器理论模型建立

根据流体力学理论,机器鱼体在流体介质中游动时所受的阻力FD为:

(2)

其中,FD为机器鱼体所受阻力;CD为在流体介质的阻力系数,其值大小取决于雷诺系数Re与流体的性质;ρf为流体密度;u为鱼体前进速度;S为鱼体在流体中的接触面积。

根据文献[13-15],理想推进器理论模型依据诱导速度(与推力方向相反)是由推进器拨水产生推力从而使得流体受到推进器作用而获得的,因此可以应用流体力学中的动量定理来研究因推进器作用而具有的水动力性能,对于机器鱼驱动模型,已有文献大多仅考虑尾鳍作为机器鱼体产生前向动力的唯一推进器,本文设定机器鱼推进器为摆动的尾鳍(摆动的尾鳍固联舵机)及部分鱼身(含有舵机模块)。根据动量定理,Δt时间内作用在流体上的力等于Δt时间内流体动量的增量,即

FiΔt=mfivai

(3)

其中,Fi为第i(i=1,…,4)个推进器(尾鳍及部分鱼身)产生的推力;Δt为推进器推进的时间;mfi为第i个推进器扫过的流体质量;vai为第i个推进器的横向拍动速度。

(3)式中推进器的横向拍动速度vai取值与推进器的运动规律相关,假设第i个推进器的运动规律为:

(4)

其中,li为第i(i=1,…,4)个推进器左右拍动的位移;Ai为第i个推进器的振幅;ω为推进器绕轴摆动时的角速度(在此设定4个推进器角速度相同);ξi为第i个推进器与流体流动方向的摆角;Ψi为第i个推进器的摆角幅度;φi为第i个推进器与第1个推进器的摆动角度差。

(4)式中,推进器绕轴摆动时的角速度ω为绕轴摆动频率f(设定4个推进器角速度相同,因此摆动频率相同)的函数。则第i个推进器的横向拍动速度vai为:

vai=ii=2πfAicos(2πft)

(5)

第i个推进器扫过的流体质量mfi为：

mfi=ρfVi

(6)

其中,mfi也为扫水质量;ρf为流体密度;Vi为第i个推进器摆动过程中扫水的体积,且有：

Vi=Sicosξi(vai-vtanξi)Δt

(7)

其中,Si为第i个推进器的单侧面积;v为流体流动速度。

基于理想推进器理论的机器鱼推进力学模型如图6所示。

图6 基于理想推进器的机器鱼运动力学模型

根据机器鱼体运动力学模型有：

(8)

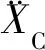
[2πfAicos(2πft)-vtan(Ψisin(2πft-φi))]×

(9)

为实现机器鱼游动模型方程的求解,引入机器鱼鱼体及流体介质相关数据,见表2所列。

表2 机器鱼鱼体及流体介质参数

3.2 机器鱼游速影响因素分析

3.2.1 机器鱼游速与驱动方式的关系

利用Matlab/Simulink建模,求解(9)式中的常微分方程,得到对应图3的15组不同舵机驱动方式机器鱼纵向游动速度,机器鱼体游动过程中的速度瞬态历程变化曲线如图7所示。

图7 第1组～第15组游动方式的速度曲线

将15组驱动方案以舵机驱动数量为分类依据可分为如下4类：① 仅1组舵机驱动的为第1组；② 含2组驱动舵机的为第2组、第3组；③ 具有3组驱动舵机的为第4组～第7组；④ 具有4组驱动舵机的为第8组～第15组。图7中,有多组驱动方式的游动速度曲线相互重合。4类驱动方式中各组内每组舵机数量一致,差别在于舵机相位差不同,推测曲线重合的原因是舵机相位差对机器鱼游速的影响较小。

3.2.2 机器鱼游速与舵机相位差的关系

为此,以第2组～第3组、第4组～第7组,第8组～第15组为对象,分别绘制出这3种驱动方案的机器鱼游动速度曲线，如图8所示。

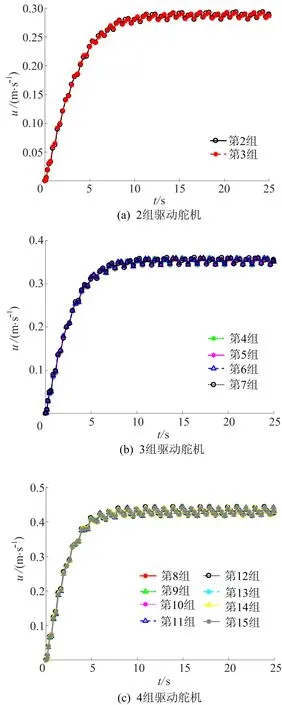
图8 多组驱动舵机游速曲线

由图8可知,当驱动舵机数量确定后,在相同摆幅和频率下,舵机之间的相位差对于机器鱼游动速度影响较小,而驱动舵机数量对鱼速游动起决定性影响,这是由于增加驱动舵机数量会使鱼身触水面积增大,摆动中鱼身纵向运动的流体推进力增加,导致机器鱼游速提高。

3.2.3 机器鱼游速与振幅频率的关系

得出鱼速与舵机数量及其摆动相位差的关系后,为进一步研究基于舵机驱动的运动参数对机器鱼游动行为的影响,选择第15组舵机驱动方案。改变舵机绕轴摆动频率f和振幅Ai,取摆动频率为1.0～2.0 Hz,振幅分别为0.10、0.15、0.20 m,以摆动频率为横坐标、稳态游速为纵坐标,得到机器鱼游速与摆动频率、振幅的关系，如图9所示。图9中,i=1,2,3,4。

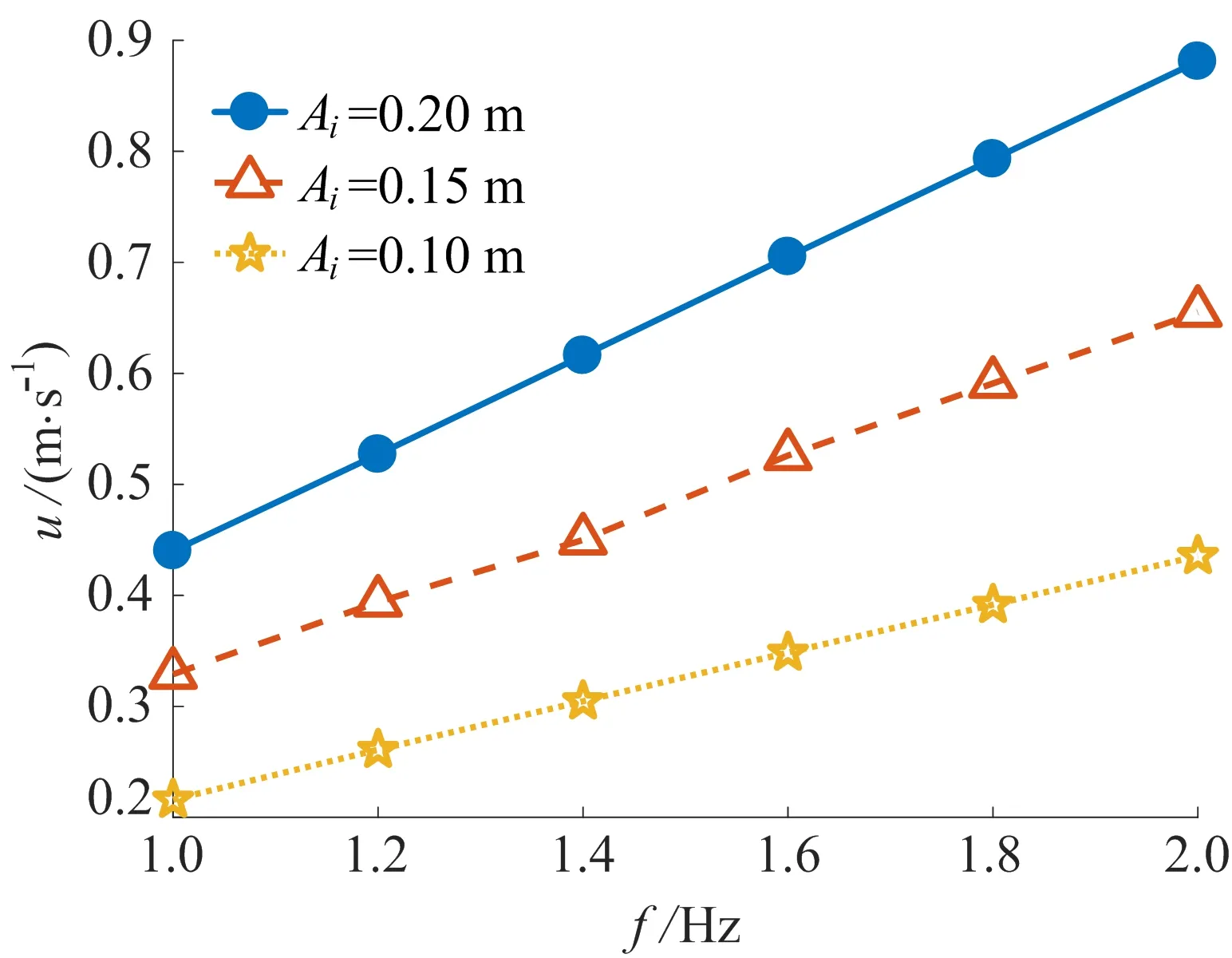
图9 机器鱼游速与振幅、频率的关系

由图9可知,在舵机摆动振幅一定时,机器鱼的稳态游速与舵机频率成正比关系；而当频率恒定时,机器鱼稳态游速随着振幅的增加而增加。

图7～图9表明,基于舵机驱动的机器鱼,其游速主要取决于舵机数量、舵机摆动振幅和舵机摆动频率,而舵机之间运动相位差对游速影响较小,可忽略不计,舵机之间的驱动相位差主要影响机器鱼包络线是否接近真实鱼类包络线。

3.3 各类机器鱼游速模拟验证

结合图7、图8,依据已有的研究结果，将鱼类划分为箱鲀科、鲔科、鲹根、鳗鲡科4种运动模式。根据从箱鲀科到鳗鲡科鱼类游速逐渐增大再减小的结论[2],为验证基于多舵机串联驱动的机器鱼运用理想推进器推进理论的正确性,参照前文所述舵机驱动的15种方案,将第1组驱动方式模拟为箱鲀科运动模式、第2组～第3组模拟为鲔科运动模式、第4组～第7组模拟为鲹科运动模式、第8组～第15组模拟为鳗鲡科运动模式。同时结合自然界中鳗鲡科鱼类鱼体身体触水面积较小的特点,将4个舵机的单侧接触面积设置为第8组～第15组中所设面积的1/2,得到的鱼速模拟结果如图10所示。

图10 4类推进模式机器鱼游速模拟

由图10可知,4类推进模式的机器鱼游速模拟结果符合自然界中箱鲀科、鲔科、鲹科、鳗鲡科鱼类的游速规律,从而说明利用舵机驱动模式,控制驱动舵机数量,可实现多种鱼类对游速的模拟。

4 结 论

(1) 本文利用多舵机驱动方案,建立了机器鱼驱动结构模型,运用虚拟样机技术进行了机器鱼动力学仿真；通过多种驱动方式波幅包络线图谱发现，基于多舵机且相互之间具有相位差的驱动方式会使机器鱼包络线更加符合真实鱼类身体推进波波幅包络线。结合Matlab/Simulink建模工具求解出的多种驱动模式机器鱼游速结果表明,相对于舵机数量对机器鱼游速的较大影响程度,舵机之间的摆动相位差对机器鱼游速影响极小,影响程度可忽略不计。

(2) 通过分析机器鱼不同驱动方式所得的游速发现，增加舵机数量可使机器鱼的游动速度加快,推测其主要原因是增加的舵机数量扩充了鱼体触水面积,且机器鱼游动时鱼身摆动会产生推力影响机器鱼自主游动速度。

(3) 依据理想推进器理论,本文建立了鱼类动力学模型,通过Matlab/Simulink仿真,将所得结果与自然界中4种推进模式鱼类对比,结果表明理想推进器理论可进行对基于舵机驱动的箱鲀科、鲔科、鲹根、鳗鲡科鱼类游速的模拟仿真。