Ⅱ型弹条模态特征模拟分析与试验研究

刘晓丹 肖俊恒 孙林林 闫子权 崔树坤

（1.中国铁道科学研究院研究生部，北京 100081； 2.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081）

钢轨扣件是轨道结构中联结钢轨与支承结构的重要部件。其主要作用是保持和调整轨距及轨向，提供纵向阻力并防止钢轨爬行，提供弹性，在一定范围内调整钢轨高低位置等［1-2］。扣件失效会加剧轮轨间动力响应，甚至引起脱轨，造成严重的行车事故。在铁路运营过程中，车轮和钢轨之间的周期性磨耗会引起车辆轨道系统之间的剧烈振动，轮轨之间的高频振动会对扣件产生不利影响，造成扣件弹条断裂等严重伤损。弹条断裂会减弱扣件对钢轨的约束，加速轨道结构的破坏，严重影响列车行车安全［3］。

针对扣件弹条在轮轨激励作用下的断裂问题，肖俊恒等［4］分析了钢轨波磨和车轮多边形磨耗引起的轮轨高频激励，揭示了轮轨激励与弹条固有频率接近时引起弹条共振从而导致断裂的机理；肖宏等［5］通过建立e 型扣件精细化模型，对弹条在自然状态和服役状态下的模态振型、谐响应特征进行分析，从时域角度揭示了e 型弹条断裂的根本原因；费玉坤等［6］建立弹条I型扣件的有限元模型，分析其固有模态特征，得出钢轨波磨和车轮多边形引起的轮轨高频振动导致了弹条共振从而折断；高晓刚等［7］针对PR 型弹条，通过弹条伤损区间钢轨动态位移测试及波磨检测分析，得到轮轨作用的激励频率，与弹条安装状态下模态对比，发现在730 Hz 左右弹条模态频率与轮轨激励频率相近，认为轨道不平顺、轮轨激励与弹条振动导致的共振是异常伤损的主要因素；孙林林等［8］以SKL 15 弹条为例，研究了弹条模态特征的试验测试方法，包括测点的布置，传感器的选择以及如何消除加速度传感器产生的附加质量对弹条固有频率的影响；尚红霞［9］建立了高速铁路福斯罗扣件的有限元模型，研究不同波磨状态对弹条最大等效应力的影响规律；赵才友等［10］现场测试了弹条在不同运营条件下的工作模态，指出弹条的前两阶固有模态容易被激起共振，在设计时应重点考虑；崔树坤等［11］采用锤击激励法对WJ-8配套使用的W1 型弹条的模态特征进行了试验研究，结果表明标准安装状态下W1 型弹条在0～1 000 Hz 范围内具有2阶模态。

综上可以看出，许多学者对弹条模态特征识别方法做了大量的研究工作，但鲜有学者把理论与试验方法结合起来。因此采用有限元模态分析理论和试验方法研究Ⅱ型弹条固有振动特性，得到其敏感频率范围，以便从深层次揭示轮轨间相互作用对弹条断裂的影响机理，为研究轮轨之间相互作用及解决弹条断裂问题提供依据，为既有弹条的优化设计及新型弹条的设计开发提供理论支撑。

1 Ⅱ型弹条有限元模态分析

1.1 有限元分析模型

通过拾取弹条中心线空间坐标点的精确位置，利用有限元软件ANSYS 建立Ⅱ型弹条有限元模型，如图1 所示。为充分考虑弯曲和扭转变形，采用Beam188单元模拟弹条。

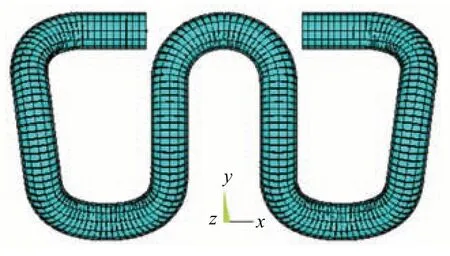
图1 弹条有限元模型

1.2 边界接触刚度计算

采用经典赫兹接触理论来确定轨距挡板和螺旋道钉与弹条间接触刚度的大小。根据接触特征，按接触类型为2个椭圆体接触计算弹条与轨距挡板和平垫圈之间的接触刚度。2 个椭圆体相互接触时，接触区域呈椭圆形。接触情况如图2所示。

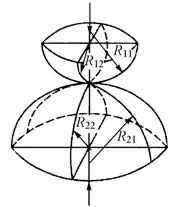
图2 2个椭圆体接触情况示意

椭圆的长短轴半径a，b以及2 个物体的相对位移δ计算公式为［12］

式中：α，β，λ为系数；P为接触力；R11，R12，R21，R22分别为弹条及与弹条接触部件在接触区域2个平面内的主曲率半径；μ1，μ2分别为弹条和接触部件的泊松比；E1，E2分别为弹条和接触部件的弹性模量。

Ⅱ型弹条的标准扣压力为10 kN，由P/δ即可求出接触刚度K。

扣件部件材料参数见表1。

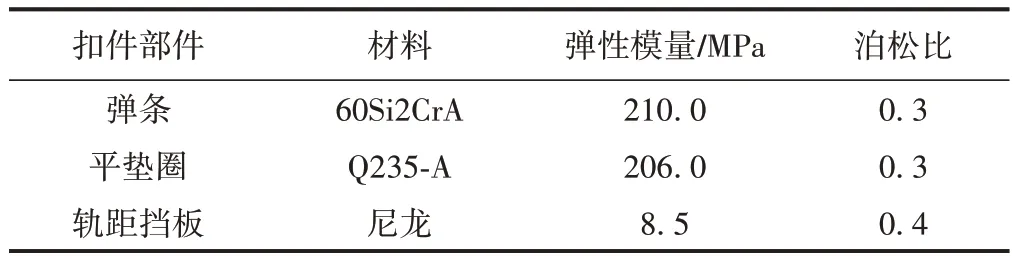
表1 扣件部件材料参数

由式（1）—式（4）及表1计算得到扣件各部件之间的接触刚度，见表2。

表2 扣件各部件间接触刚度 kN·mm-1

1.3 有限元结果分析

由文献［2］和文献［4］可知，弹条由于共振产生伤损的频率大多在500～650 Hz，且轮轨激励作用传递至弹条上的振动频率大部分在1 500 Hz以内。因此研究Ⅱ型弹条在0～1 500 Hz频率范围内的模态特征。

1.3.1 弹条自由状态下模态

弹条自由状态下模态特征可以揭示其在无边界约束条件下结构本身的模态特征。弹条自由状态下0～1 500 Hz 频率范围内的模态振型及固有频率见图3。其中，黑色实线和红色实线分别代表弹条未变形和变形后状态。

由图3 可以看出：在0～1 500 Hz频率范围内，Ⅱ型弹条第1 阶模态振型为弹条两侧肢对称振动，弹条中肢与侧肢上下反对称振动，振动节点为弹条支承端；第2 阶模态振型为弹条扣压端与支承端反向振动，两侧扣压端反对称振动，振动节点为弹条中肢顶端；第3阶模态振型为弹条两侧肢对称上下振动，弹条中肢与侧肢上下反对称振动，振动节点为弹条支承端；第4阶模态振型为弹条扣压端对称上下振动，弹条中肢与扣压端反对称上下振动；第5 阶模态振型为弹条侧肢反对称外翻振动。

1.3.2 弹条标准安装状态下模态

弹条标准安装状态下模态特征可以揭示其在正常服役状态下的模态特征。弹条标准安装状态下0～1 500 Hz 频率范围内Ⅱ型弹条的模态振型及固有频率见图4。

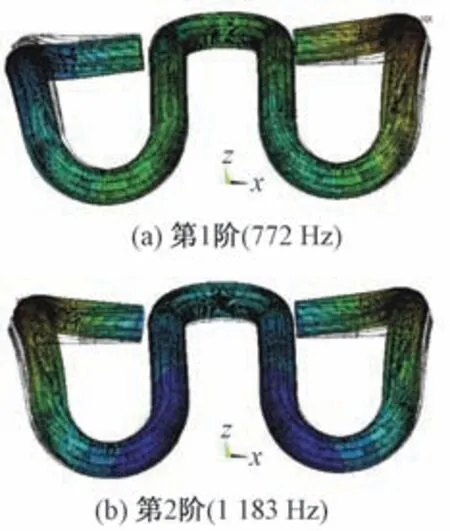
图4 弹条标准安装状态下模态振型及固有频率（数值模拟）

由图4 可以看出，标准安装状态下Ⅱ型弹条第1阶模态振型为两侧肢以扣压端和支承端为支点反对称外翻振动；第2 阶模态振型为两侧肢以扣压端和支承端为支点对称外翻振动。与自由状态下的弹条模态特征相比，标准安装状态由于在扣压端、支承端及紧固位置与其他部件接触而增加了相应的约束，提高了弹条各阶频率并改变了相应的模态振型。

2 Ⅱ型弹条室内试验验证

2.1 试验方法及仪器选择

采用锤击法拾取Ⅱ型弹条模态特征，其具有激励频率带宽较宽、时效性高、操作空间要求小等优点。锤头采用橡胶头，试验通过3 次测量取平均值以减小误差。

常用的模态试验拾振传感器主要有加速度传感器、声压传感器和激光传感器3 种。加速度传感器相干函数较好，信号可信度较高，但是会对弹条产生附加质量；声压传感器可有效捕捉弹条振动响应，同时对弹条边界无任何影响，但是对外界环境噪声敏感，在低频处的干扰较强；激光传感器同声压传感器一样，可有效捕捉振动响应同时不产生附加质量，缺点是对外界环境温度敏感，所需工装复杂，因此并不适用于现场测试。

针对弹条自由状态下模态，选择在无噪声的环境中利用声压传感器进行测试。针对弹条标准安装状态下模态，由于实验室中环境条件较差，不适合用对环境噪声敏感的声压传感器，因而选用加速度传感器进行测试。

2.2 试验方法

为有效拾取Ⅱ型弹条的模态特征，在整个弹条均匀布设测点，如图5所示。

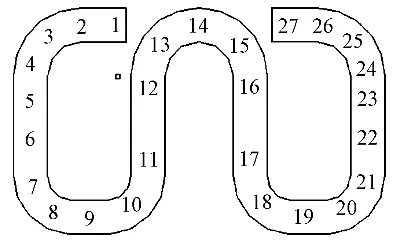
图5 弹条锤击激励点分布

在弹条自由状态下模态测试过程中，为了避免边界条件对测试造成影响，将弹条放置在海绵上进行试验，将声压传感器放置于弹条正前方。

在弹条标准安装状态下模态测试过程中，将加速度传感器放置于22 号测点。该测点加速度响应幅值较其他测点高，便于观测。

2.3 试验结果分析

2.3.1 弹条自由状态下模态

Ⅱ型弹条自由状态下的频响函数集总曲线见图6。

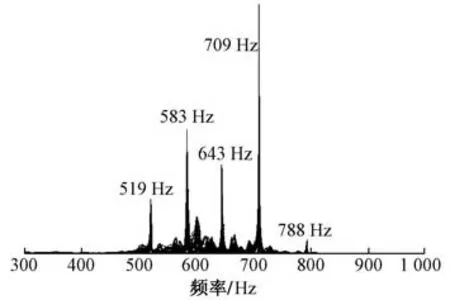
图6 弹条自由状态下的频响函数集总曲线

从图6 可以看出，在0～1 500 Hz 频率范围内Ⅱ型弹条自由状态下模态有5 阶，其固有频率分别为519，583，643，709，788 Hz，其振型见图7。

对比图3 和图7 可以看出：数值模拟与试验测试的Ⅱ型弹条自由状态下模态振型一致；第1 阶—第5阶模态的固有频率分别相差5.49%，1.22%，2.55%，2.46%和4.10%。Ⅱ型弹条自由状态下模态频率数值模拟结果略低于试验结果。主要是由于试验中将弹条放置在海绵上以模拟自由边界条件，海绵对弹条仍有一定的支承刚度。但数值模拟结果和试验结果相差基本在5%以内，且模态振型相同，验证了有限元模态分析方法的正确性。

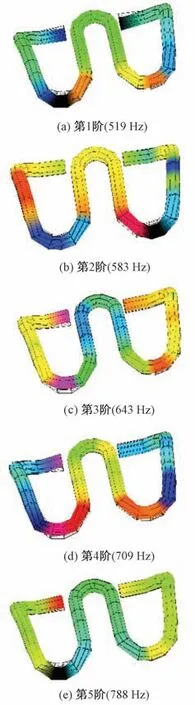
图7 弹条自由状态下模态振型及固有频率（试验测试）

2.3.2 弹条标准安装状态下模态

Ⅱ型弹条标准安装状态下的频响函数集总曲线见图8。

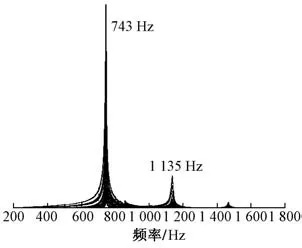
图8 弹条标准安装状态下的频响函数集总曲线

从图8 可以看出，在0～1 500 Hz 频率范围内Ⅱ型弹条标准安装状态下模态有2 阶，其固有频率分别为743 Hz和1 135 Hz，其振型见图9。

图9 弹条标准安装状态下模态振型及固有频率（试验测试）

对比图4 和图9 可以看出：数值模拟与试验测试的Ⅱ型弹条标准安装状态下模态振型相同，第1 阶和第2 阶模态的固有频率分别相差-3.76%和-0.41%。Ⅱ型弹条标准安装状态下模态频率试验结果略低于数值模拟结果，原因是试验中拾振采用的加速度传感器对弹条施加了一定的附加质量，但加速度传感器质量相对于弹条质量较小，其对弹条模态频率的影响较小。因此，建立的有限元模型能够准确描述弹条的实际结构，模型采用的边界条件及模拟方法能够准确模拟弹条的组装状态，进一步验证了有限元模态分析方法的正确性。

3 结论

本文根据Ⅱ型弹条实际空间尺寸建立其精细化有限元模型，对其自由状态和标准安装状态下模态特征进行了有限元分析，并进行了室内试验验证。得到以下主要结论：

1）在0～1 500 Hz频率范围内，Ⅱ型弹条在自由状态下有5 阶模态，其固有频率分别为492，576，627，692，757 Hz；在标准安装状态下有2 阶模态，其固有频率分别为772 Hz和1 183 Hz。

2）在0～1 500 Hz频率范围内，有限元模态分析方法和室内试验方法得到的Ⅱ型弹条模态固有频率误差均在5%以内，模态振型均一致，两者均可有效拾取Ⅱ型弹条的模态特征。

3）当钢轨波磨或车轮多边形导致轮轨激励频率接近弹条标准安装状态下的固有频率时，应对钢轨及时打磨或对车轮及时镟修。