高速铁路灾害监测系统风报警解除时限优化方法

赵方霞

（中国铁道科学研究院集团有限公司电子计算技术研究所，北京 100081）

为保证高速列车运行安全，从京津城际铁路开始，我国铁路部门随工程建设同步建设了高速铁路自然灾害及异物侵限监测系统（简称灾害监测系统）［1-2］。风监测系统作为其中的一个子系统，为列车运行提供风速报警信息及列车运行管理建议。目前，根据现有的铁总运〔2014〕146 号《高速铁路自然灾害及异物侵限监测系统铁路局中心系统总体方案（暂行）》大风报警规定［3］，当风速低于报警阈值并连续10 min 后解除当前报警级别。但对于不同地区的线路，大风规律存在较大的差异，统一规定大风报警解除时限为10 min不尽合理，应该在考虑列车运行安全的前提下，综合考虑大风报警解除时限对列车运行效率和大风报警处置工作量的影响，寻找最优的大风报警解除时限。

各国家对风报警解除时限开展了相应的研究［4］。日本传统的风管制措施为［5］：在观测点风速超过标准限值的时刻立即开始；在观测点最后1 次风速超过标准限值时刻的30 min 后结束。传统风管制报警解除时限为30 min 是基于对以往事故的处理经验而制定的，但作为现今风报警的基础手段则相对保守。因此，考虑到大风天气里列车运行往往由于顾及高安全性而延误，导致交通状况不稳定，日本研究开发了强风预警系统［6］。该系统可以在实测风速和最大预测风速两者均低于管制设定值时解除管制，平均缩短管制时间20%～30%，大大提高了铁路运营效率［7］。法国风监测报警采用风速和风向相结合的方式，系统可预测5 min 内的风速和风向，风速达到报警解除条件并持续15 min后解除当前报警［8］。

我国的高速铁路灾害监测系统还未实现大风的预警功能，为了提高列车运行安全，需要进一步对大风预警规则进行优化分析，而大风报警解除时限优化分析是其中的一个重要方面。

本文基于高速铁路沿线风监测系统报警数据，考虑报警解除时限对报警次数和影响时长的影响，建立高速铁路灾害监测系统风报警解除时限优化模型；并在考虑线路的繁忙程度以及受大风影响程度的基础上进行数值求解，得到不同线路的最优风报警解除时限值，提高高速铁路防灾系统的运用效果及列车的运行效率。

1 风报警解除时限优化方法

大风的发生存在一定的规律性，但单纯从规律分析无法定量给出报警解除时限的最优值，故此节对报警解除时限进行建模分析，从定量的角度给出报警解除时限的最优值。

当报警解除时限发生变化时，相应的报警次数和影响时长（报警持续影响时间）也会发生变化，其中线路报警次数过高会增加调度人员的处置工作量，线路影响时长过长会影响列车的运行效率。因此优化报警解除时限须要考虑报警次数和影响时长的影响，建立优化模型。

1.1 定义及符号

定义1：高速铁路灾害监测系统从风速低于报警阈值到报警解除之间持续的时间，称为报警解除时限。如：根据相关规定［3］，当风速超过报警阈值并连续10 s后，发出报警；当风速低于报警阈值并连续10 min后解除报警。此处10 min即为报警解除时限。

定义2：高速线路某区域某个时间段内灾害监测系统发出的报警条数即为报警次数，其中报警升（降）级1 次，报警次数增加1 次。报警次数越多，报警处置的工作量就越大。

定义3：高速线路某区域某时间段内灾害监测系统从发出报警到报警解除所有持续时间段的累计称之为影响时长。影响时长越短，列车运行的效率就越高。

本文中用到的符号及其所表示的含义见表1。

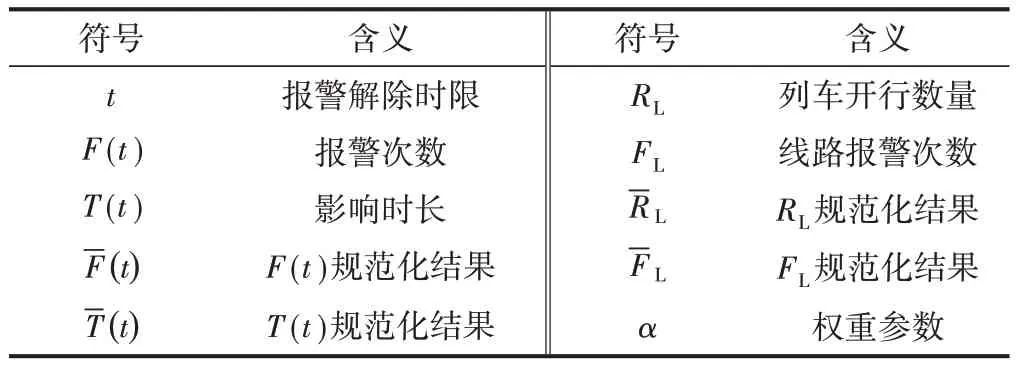
表1 符号表示

1.2 模型

报警次数和影响时长是报警解除时限的函数，并且报警次数F(t)是递减函数，即F'(t)＜0；影响时长T(t)是递增函数，即T'(t)＞ 0。

优化目标是在保证列车运行效率的前提下使得报警处置工作量尽可能少。根据报警次数和影响时长的定义，尽可能使得报警次数少，即minF(t)，可以减少调度处置工作量；尽可能使得影响时长短，即minT(t)，可以提高列车运行效率。然而这2个目标是相互制约的，即减少报警次数会增加影响时长，缩短影响时长会增加报警次数。因此须要根据各条线路的特性（此处考虑列车开行数量和线路报警次数），找到最优的报警解除时限t*。为了使报警次数和影响时长之间具有相同的量纲，对报警次数和影响时长进行规范化处理，使报警次数和影响时长变为无量纲的指标。其中(t)为T(t)的规范化结果(t)为F(t)的规范化结果，则目标函数表示为

其中，权重参数α的取值须考虑如下2个因素：

1）线路的繁忙程度

可以用列车开行数量RL反映线路的繁忙程度，繁忙的线路应尽量使影响时长短一些，从而增加运行效率；不是很繁忙的线路应尽量减少报警次数，从而减少调度人员的处置工作量。

2）线路受大风的影响程度

可用线路报警次数FL反映线路受大风的影响程度，对于受大风影响大的线路应尽量减少报警次数；而受大风影响小的线路应尽量减少影响时长，提高线路的运行效率。

为了使线路繁忙程度和受大风影响程度之间具有相同的量纲，对列车开行数量和线路报警次数进行规范化处理，使得列车开行数量和线路报警次数变为无量纲的指标。其中为RL的规范化结果为FL的规范化结果。

综合考虑线路繁忙程度和受大风影响程度，权重参数α的计算公式为

其中，0 ≤α≤ 1。α→ 1 表示线路趋于繁忙；α→ 0表示线路受大风的影响加大。

1.3 求解算法

为了求解式（1）的目标函数，本文基于高速铁路沿线历史数据，采用离散化方法进行计算，具体计算步骤如下：

步骤1 对影响时长T(t)和报警次数F(t)进行规范化处理，使得报警次数和影响时长变为无量纲指标。

步骤2 对列车开行数量RL和线路报警次数FL进行规范化处理，得到取值。

2 计算实例

2.1 不同线路报警解除时限优化结果

利用上述报警解除时限优化模型及求解算法，选取线路1、线路2 和线路3 共3 条线路对报警解除时限进行优化分析。表2 给出了3 条线路的列车开行数量、线路报警次数情况及权重参数α的取值。

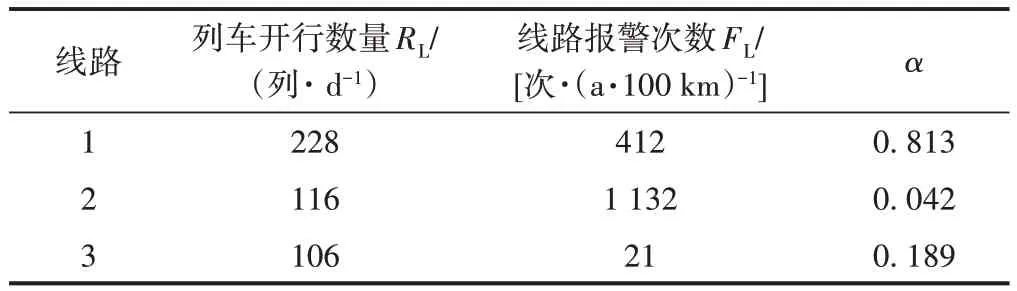
表2 列车开行数量、线路报警次数及权重参数

将线路1 沿线172 个风监测点自2016 年1 月至2017 年 9 月、线路 2 沿线 23 个风监测点自 2016 年 1 月至 2016 年 6 月、线路 3 沿线 32 个风监测点自 2015 年 9月20 日至2017 年1 月9 日的大风报警数据按报警解除时限为1～30 min 进行模拟报警，统计3 条线路的报警次数和影响时长，结果如图1 所示。可以看出随着报警解除时限的增加，报警次数是单调递减的，影响时长是单调递增的。因此，无法同时满足报警次数和影响时长同时降低的目标，必须在两者权衡下寻求最优的报警解除时限。

图1 3条线路报警次数和影响时长变化情况

基于线路1—线路3的历史监测数据，求解报警解除时限目标函数（参见式（1）），得到其变化趋势如图2所示。可以看出，当报警解除时限分别为5，21，13 min时，线路1—线路3 的目标函数分别达到最小值，即线路1—线路3 的最优报警解除时限分别为5，21，13 min。

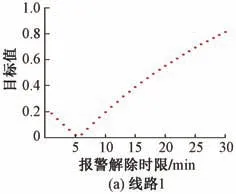
图2 3条线路目标函数变化情况

线路1—线路3进一步采用最优报警解除时限，报警次数和影响时长的变化情况见表3。

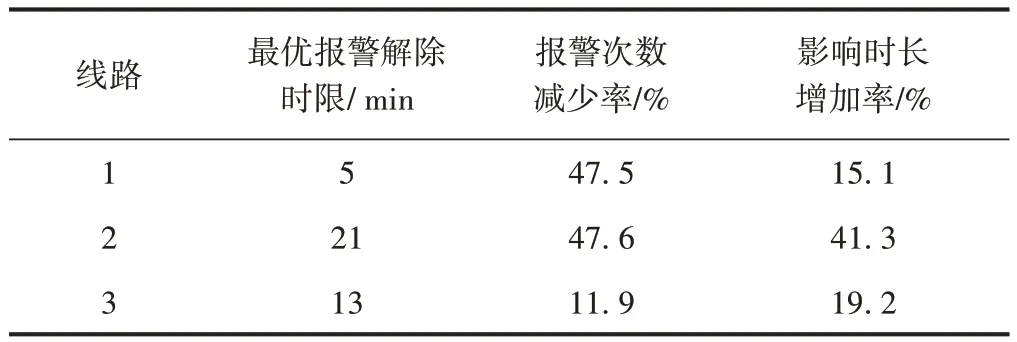
表3 优化后报警次数和影响时长变化情况

从表3 可以看出，由于线路1 属于繁忙线路，运行效率更加重要，因此优化后影响时长增加率仅为15.1%；线路2 运行效率和处置工作量几乎同等重要，因此影响时长增加率和报警次数的减少率差不多；对于线路3 更看重报警处置工作量，因此增加了19.2%的影响时长来减少报警次数。

2.2 不同铁路局报警解除时限优化结果

对于不同的线路，由于线路的特性不同最优报警解除时限也会不同；而对于同一条线路，不同区段最优报警解除时限也会随着风的特性发生变化。下面选取线路1进行分析。

线路1在铁路局A，B，C的管辖下，对线路1在3个铁路局中单独进行报警解除时限优化分析，各铁路局最优的报警解除时限如图3所示。

从图3 可以看出，对于线路1，铁路局A 和铁路局B 最优大风报警解除时限为6 min，铁路局C 最优大风报警解除时限为5 min。铁路局C 的大风报警次数较铁路局A 和铁路局B频繁，占统计数据的76%（见表4），因此，在线路1整个线路数据分析中，铁路局C大风报警数据占了主导。

图3 线路1在3个铁路局中最优报警解除时限

表4 线路1在3个铁路局中的报警情况

2.3 不同季节报警解除时限优化结果

对于同一条线路，不同季节风规律不同，线路的最优报警解除时限也会发生变化。下面选取线路2进行大风报警解除时限季节性分析，求解目标函数，得到最优报警解除时限如图4 所示。可以看出，对于线路2，1—4 季度最优报警解除时限分别为12，19，11，14 min。

图4 线路2在不同季度下最优报警解除时限

表5 线路2在不同季度下最优报警解除时限

表5 为线路2 在不同季度下最优报警解除时限。可以看出，在风季报警解除时限最优值要大一些，在非风季时最优值要小一些。由于线路2季节风比较明显，通过对大风报警进行季节性分析，可以得到报警解除时限不同季节的最优值，进而针对不同季节对报警解除时限进行设置，可以提高列车的运行效率。

3 结论

本文建立了高速铁路灾害监测系统风报警解除时限优化模型，通过选取3条典型线路进行综合分析，得到结论如下：

1）对不同的线路，由于线路特性不同，报警解除时限也不同，其中线路1—线路3最优报警解除时限分别为5，21，13 min。

2）对于同一条线路，不同铁路局管段最优报警解除时限也不同，对于线路1，铁路局A 和铁路局B 最优报警解除时限为6 min，铁路局C最优报警解除时限为5 min。

3）对于同一条线路，不同季度下最优报警解除时限也不同，对于线路2，1—4 季度最优报警解除时限分别为12，19，11和14 min。