橡胶粘弹性分数导数本构模型合理性研究

何松林，俞 安，任 杰

(昆明学院 机电工程学院，云南 昆明 650214)

橡胶是具有多种特殊性质的材料，在工业中有广泛的应用.为了在工程实践中充分利用各种橡胶材料，弄清楚各类橡胶材料的力学性质就显得格外重要[1].橡胶既具有超弹性又具有粘弹性，为描述其力学性质，出现了多种本构模型，而建立模型几乎都采用对具体材料或结构的实验数据进行非线性最小二乘拟合的方法，并依据拟合精度的要求确定参数个数[2-7]，对于工程应用而言，这样的做法无可厚非，特别是现代计算机具有强大的功能，很容易支持采用这些模型进行工程建模，但此方法又似乎缺乏对材料性质产生机制及如何更好描述材料性质等方面的探究.因此，本文拟通过对仅受与分数阶导数项成正比的力作用的质点运动微分方程的求解，对由橡皮筋和质量块构成的橡皮筋振子自由振动进行理论分析和实验观察，以说明采用分数导数本构模型描述橡胶材料的粘弹性是更加合理的选择.

1 橡胶材料本构模型现状

橡胶材料的力学性质非常复杂，其既具有超弹性也具有粘弹性.在静态或准静态时，其主要表现出非线性弹性和蠕变、松弛等静态粘弹性行为，而在动态时则表现出力学性质随载荷加载快慢变化的动态粘弹性行为.为描述这些性质，出现了专门针对其非线性弹性的超弹本构模型[2，5，6]，以及针对其粘弹性的粘弹本构模型[3]和试图全面描述其性质的超弹-粘弹本构模型[4，7].超弹本构模型数量众多，但都可以归为采用统计热力学和连续介质力学确定应变能函数两大类.粘弹性本构模型的建立主要是根据实验数据拟合出数学表达式，这种方法能够高精度逼近实验曲线，但模型参数没有明确的物理意义.至于超弹-粘弹本构模型，则是将已有的超弹和粘弹模型结合起来去处理具体材料的力学性质.

材料的结构决定其性质是自然科学的重要思想，因而采用基于对材料结构认识所作的假设而推导出的本构模型应该是更合理的选择，也许此模型对实验数据的拟合精度不够高，但可通过对假设的修正或增加相应的条件逐渐改善.而仅仅采用拟合实验数据的做法，可能会削弱对材料力学性质产生的机理的探究，且拟合得到的关系式难以在与实验条件差异较大的情况下应用.此外，能反映本质规律的表达式应该是简捷的，换句话说，太多个参数的本构方程可能不能揭示材料的本质特征.

当探讨涉及橡胶粘弹性问题时，标准机械模型是经常采用的一类本构模型[8].此模型将粘弹性视为既有弹性又有粘性，采用弹簧模型描述弹性，用牛顿粘壶描述粘性.不同数量的弹簧和粘壶串联或并联构成不同的模型，比如：一个弹簧和一个粘壶并联构成Kelvin-Voigt模型；一个弹簧和一个粘壶串联构成Maxwell模型；一个弹簧和一个Kelvin-Voigt模型串联构成三元件模型等.标准机械模型在工程建模中有大量的应用，但该模型将高分子材料特有的统一粘弹性用粘性和弹性的不同组合进行描述，存在无法探究结构与性质关系的不足.当然，这主要是由于难以找到直接描述粘弹性的数学工具而造成的.

近年来，随着分数阶微积分的发展，它也被用来处理粘弹性问题[9-12]，很多工作已证明分数阶导数模型(即用Abel体代替牛顿粘壶后构成的机械模型)对实验数据的拟合有更好的效果.虽然有采用分数阶导数模型进行橡胶材料构件建模分析研究的报道，但分数导数模型是否能更好地描述粘弹性，它是否更接近粘弹性的本质等问题都没有解决，加之人们对分数阶微积分的相对陌生，多数实际工程建模仍采用传统机械模型.

2 粘弹性力可以由分数导数项表示

设一个质点，仅仅受到与分数阶导数项成正比的力的作用，由牛顿第二定律可得质点得运动微分方程为

(1)

其中k为常数，0<α≤1是Caputo分数阶导数的阶数.

(2)

利用二阶导数及Caputo分数阶导数Laplace变换的性质[13]得

s2X(s)-sx0-v0+k[sαX(s)-sα-1x0]=0，

(3)

(4)

由Mittag-Leffler函数的Laplace变换公式

(5)

(6)

(7)

(8)

对(4)式进行Laplace反变换，并将(6)、(7)和(8)式代入，得方程(1)满足所设初始条件的特解为

x(t) =x0E2-α,1(-kt2-α)+kx0t2-αE2-α,3-α(-kt2-α)+v0tE2-α,2(-kt2-α).

(9)

由双参数Mittag-Leffler函数和Gammar函数的定义及性质可得

(10)

(11)

令j=k+1，(11)式化为

(12)

利用(12)式可将(9)式化简，得到方程(1)的解为

x(t) =x0+v0tE2 - α,2(-kt2-α)，

(13)

(13)式是方程(1)的精确解，由(13)式可看出，受到与分数阶导数项成正比的力作用的质点的位移随时间的变化只与质点的初速度有关，与初始位移没有关系；若质点初速度为零，质点将静止在初始位置.从这个角度来看，与分数阶导数项成正比的力是一种阻力.

为考察在不同阶数的分数阶导数力作用下质点的位移随时间的变化情况，在x0=1 m，v0=1 m/s，k=1sα-2的情况下，对不同α取值，按(13)式作出运动曲线，如图1所示.

图1 不同阶数的分数阻尼力下质点的位移时间图

从图1可看出，随α值由1逐渐向趋近于0，质点的运动由单向地趋于平衡位置，逐渐变成在平衡位置附近振荡，且振幅的衰减逐渐变慢，“振荡性”逐渐增强.

众所周知，受弹性力作用的质点(谐振子)的振动，会因为粘性阻力的存在使振幅衰减，甚至会让质点变成单向运动.因而，从上面的分析可以看出，分数阶导数项力既可提供“弹性”，同时也能提供“阻尼”，分数导数项的阶数α会影响两者的比例.

高分子材料的粘弹性使其既表现出弹性又表现出粘性，而不同材料表现出的“弹性”和“粘性”的占比各不相同，这与受分数阶导数项力作用的质点表现出的运动性质相同.由此，本文提出，采用分数阶导数项力去描述材料的粘弹性力；分数阶导数的阶数α作为表征材料粘弹性的参数，称为粘弹度，是一个由材料结构确定的无量纲实数.

3 传统Kelvin-Voigt和分数导数模型下橡皮筋振子的运动

为了考察粘弹性分数导数模型的合理性，将其与常见的Kelvin-Voigt模型进行对比研究.

设有一根轻质橡皮筋，其一端固定，另一端连接一个质量为m的质点，质点可在光滑水平面上自由运动，将这样的系统称为橡皮筋振子(图2).换句话说，仅受轻质橡皮筋作用的质点构成橡皮筋振子.

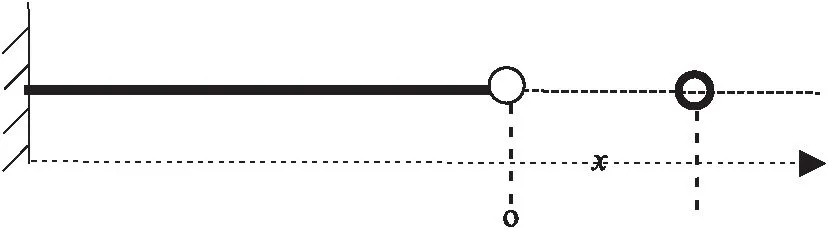
图2 橡皮筋振子示意图

如图2所示，质点在光滑水平面上自由运动，自始至终只受到橡皮筋的张力作用，将该力记为F，它由橡皮筋材料的超弹性和粘弹性形成的弹性力N和粘弹性力f叠加而成.橡胶材料的超弹性主要表现为非线性弹性，即应力随应变的变化是非线性的.但在温度和环境条件不改变，以及在一定的应变范围内，应力随应变的变化关系满足胡克定律.即橡皮筋的弹性力为

N=-k0x(t)，

(14)

其中k0称为橡皮筋的弹性系数.

若采用传统的Kelvin-Voigt模型描述橡胶的粘弹性，粘弹性被看成一个理想弹簧和一个理想粘壶串联.此模型下，橡皮筋的粘弹性力表示为

(15)

其中k1,c1是与橡皮筋材料和几何尺寸有关的常数.在此情况下，橡皮筋的张力可表示为

(16)

其中k=k0+k1.

如果采用分数导数模型，用分数阶导数项力表示橡胶材料的粘弹性力，有

(17)

则橡皮筋的张力可表示为

(18)

其中k′=k.

由(16)和(18)式可见，无论是采用Kelvin-Voigt模型还是分数导数模型，橡皮筋的张力都由两部分构成，一部分与伸长量成正比，另一部分与伸长量随时间的变化量有关系.若采用静态拉伸法测橡皮筋的弹性系数，由于伸长量随时间的变化量可视为零，可得到k′=k.

对于图2所示的橡皮筋振子，利用牛顿第二定律，考虑橡皮筋张力的表达式(16)，得到由标准Kelvin-Voigt模型得到橡皮筋振子的运动微分方程为

(19)

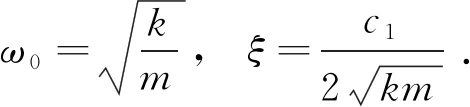
若采用分数阶导数项模型，考虑橡皮筋张力的表达式(18)，橡皮筋振子的运动方程为

(20)

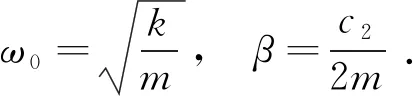
(19)式和(20)式分别是谐振子在粘性阻尼和分数阻尼下的自由振动方程.若初始条件设为

(21)

则(19)式的解为

x(t)=x0e-ξω0tcos(ωdt),

(22)

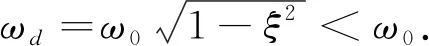
由于(20)式是含分数阶导数项的二阶常微分方程，至今没有精确解的报导.采用平均法[14]可求得其近似解析解为

(23)

若将由橡皮筋静态拉伸法测出的弹性系数k和质点质量m确定的谐振子自由振动周期设为

(24)

则按传统Kelvin-Voigt模型预测的橡皮筋振子自由振动的周期为

(25)

而按分数导数模型预测的橡皮筋振子的周期为

(26)

从上面的分析可以看出，构建一个可视为橡皮筋振子的橡皮筋质量系统，通过静态拉伸法测量出橡皮筋的弹性系数k，测量出系统的质量m后，可以算出谐振子自由振动周期T0.

观察橡皮筋质量系统的自由振动实验，测出振动周期Ts.根据Ts是大于还是小于T0，就可以判定哪一种模型更合理.

4 橡皮筋质量系统的自由振动实验

为了判断Kelvin-Voigt模型和分数导数模型哪一个更合理，用工业橡皮筋与质量块构成橡皮筋质量系统进行自由振动实验.橡皮筋长约 25 cm，横截面约为 1.2 mm×1.2 mm 的正方形，质量为m0=1.14 g.实验在复旦天欣科教仪器有限公司产的FD-GLB-Ⅱ新型焦利式秤实验仪上进行.

采用静态拉伸法测量橡皮筋的弹性系数.将橡皮筋一端固定在铁架台上，另一端与钩码架连接，在钩码架上增减钩码，并测出橡皮筋对应的长度.对测量得到的拉力增量与橡皮筋伸长量数据进行线性回归分析，得到橡皮筋的弹性系数k=9.096 8 N/m.

将橡皮筋的一端固定在铁架台上，另一端与质量为M=79.37 g 的物体(钩码及附加磁钢)连接，构成橡皮筋质量系统.将钩码向下拉离平衡位置，并由静止开始释放，观察到物体做振幅衰减的周期振动，逐渐趋向平衡位置.采用由磁钢触发霍尔开关进行次数控制的方式，用FD-CT-Ⅱ型计数计时仪多次测量4个周期对应的时间，测出橡皮筋质量系统自由振动周期为Ts=0.553 3 s.

由于空气阻力和悬挂点处的摩擦力影响很小，可忽略不计.将物体和橡皮筋的折合质量作为质点质量，则橡皮筋质量系统可视为橡皮筋振子.即上述橡皮筋质量系统的振动实验，可视为弹性系数k=9.096 8 N/m，质点质量m=M+1/3m0=79.75 g 橡皮筋振子的自由振动.由(24)式得

实验测得Ts=0.553 3 s，而T0=0.588 3 s.由此可见，Ts比T0小，约为6%.由(25)式和(26)式可知，分数导数模型比Kelvin-Voigt模型更合理.

5 小结

综上所述，本文得出仅受与分数阶导数项成正比力作用质点的运动微分方程的解析解，并依据该解析解的性质，提出可采用分数阶导数项去描述高分子材料的粘弹性力.通过对实验测量得到的橡皮筋质量系统自由振动的周期与传统的Kelvin-Voigt模型及分数导数模型预测的周期值进行分析比较，证明了分数阶导数模型更加合理.

粘弹性材料标准机械模型的思想基础是认为粘弹性是弹性与粘性的组合，而分数导数模型是用分数阶导数项直接描述材料的粘弹性，这应该更贴近材料的实际性质.采用分数导数模型去分析、解释各种高分子材料的静态和动态粘弹性效应，逐渐完善粘弹性分数导数本构模型，将是今后研究工作的努力方向.