基于环境变量的中国土壤有机碳空间分布特征*
罗 梅,郭 龙,张海涛,汪善勤,梁 攀
基于环境变量的中国土壤有机碳空间分布特征*
罗 梅,郭 龙†,张海涛,汪善勤,梁 攀
(华中农业大学资源与环境学院,武汉 430070)
研究中国土壤有机碳(Soil Organic Carbon,SOC)的空间分布特征对SOC储量估算以及农业生产管理具有重要意义。以全国第二次土壤普查2 473个土壤典型剖面的表层(A层)SOC含量为研究对象,探寻地形、气候和植被等环境因素对SOC空间异质性分布的影响;以普通克里格法为对照,利用地理加权回归、地理加权回归克里格、多元线性回归和回归克里格模型建立SOC空间预测模型;并分别绘制了中国SOC的空间分布预测图。结果表明:(1)SOC含量与年均降水量、年均温、归一化植被指数、高程以及地形粗糙指数呈极显著相关关系;(2)平均绝对估计误差、均方根误差、平均相对误差和皮尔逊相关系数等模型验证指标表明地理加权回归的预测精度优于其他模型,可以更好地绘制SOC在大尺度上的空间分布特征;(3)较高SOC含量主要分布在研究区东北部、西南部以及东南部,而西北部SOC含量普遍偏低。本文以期从大尺度上探讨土壤属性与环境变量之间的相关关系,为全国土壤属性的空间制图提供一定的解决方案和思路。
中国土壤有机碳;环境变量;地理加权回归;多元线性回归
碳是陆地生态系统最活跃的元素之一。土壤有机碳(Soil Organic Carbon,SOC)含量及其变化在全球碳循环和大气二氧化碳浓度变化中起着非常重要的作用[1-2]。地球上的碳平衡是由大气碳库、陆地系统碳库和海洋碳库三者相互作用的结果[3]。研究表明土壤是陆地系统碳库中最大的碳库且周转时间最慢,据估计当前的全球土壤有机碳库介于1 395~2 200 Pg之间[3-7],是大气碳库或陆地植被碳库的2倍至3倍。同时SOC作为土壤质量的关键指标,在土壤物理、化学和生物过程中均起着相当重要的作用[7]。为此从大尺度上探讨SOC的空间分布特征及其与环境因素之间的相关关系,对整体上掌握中国的土壤肥力状况及其在全球气候调节中所起的作用以及碳库估算具有重要意义。
SOC含量和周转率主要受土壤形成因素的影响,这些因素相互作用且具有时空差异性,为此SOC表现出很强的空间异质性[8],导致SOC的空间分布特征复杂且不确定。目前估算SOC含量的方法主要有两大类,一是测量和乘法,二是土壤景观模型[9]。其中土壤景观模型主要以区域插值模型、回归拟合模型和机器学习三种模型应用较多,综合考虑了SOC的空间变异性和依赖性以及各种环境因素的影响[9]。自20世纪50年代以来,我国研究人员进行了大量的野外调查,包括全国两次土壤普查,汇集了大量土壤数据资料用来了解和掌握中国土壤属性的空间分布特征[10]。一些研究人员对我国SOC储量和不同尺度下SOC空间分布特征进行了诸多探索性研究,尝试去捕捉SOC在空间和时间上影响的局部和全局变化[11]。许多辅助变量已被用于构建区域和国家尺度的SOC空间模型[12-14]。
为定量探索SOC与环境因子之间的关系,从而有效绘制SOC的空间分布,克里格法和回归模型得到了广泛的应用。普通克里格(Ordinary Kriging,OK)是常用的插值方法之一,但是其难以融合辅助变量的解释作用。多元线性回归(Multiple Linear Regression,MLR)和回归克里格(Regression Kriging,RK)是全局回归模型,主要限制在于其假设目标与解释变量之间的关系在整个空间内是同质性的[15]。赵永存等[16]运用MLR、RK和泛克里格预测河北省SOC密度的空间分布发现RK预测效果最好。Watt和Palmer[17]采用RK较好地估算了新西兰表层土壤的碳氮比。地理加权回归(Geographically Weighted Regression,GWR)作为绘制土壤属性的局部回归模型,不仅考虑了研究目标的空间异质性和变异性,还考虑了解释变量之间的空间不稳定关系[18]。Scull[19]利用气候因子作为自变量,发现GWR较MLR能更好地预测包括SOC在内的几种土壤属性。地理加权回归克里格(Geographically Weighted Regression Kriging,GWRK)是GWR的扩展,可以捕获GWR估计残差的空间分布特征和趋势[20]。Liu等[21]比较了几种空间预测模型,认为GWRK是绘制SOC密度的有效模型,局部模型较全局模型的预测结果更加合理。
本文选择中国土壤表层(A层)有机碳作为研究对象,以气候、植被和地形因子作为辅助变量,利用多种预测模型(OK、MLR、RK、GWR以及GWRK)探讨SOC与环境变量在大尺度上的相关关系,定量评价不同模型的建模结果,寻找最优的预测模型并进行空间制图,以期为土壤属性在国家尺度上的精确预测制图和分析土壤属性的空间分布特征提供一定的参考,从而更好地服务于区域尺度碳库估算和农业生产管理。
1 材料与方法
1.1 土壤数据
本文所采用的土壤基础数据来自全国第二次土壤普查时采集的土壤数据,这些数据资料汇总于《中国土种志》(共6卷)。据此,本文整理了共2 473个土壤典型剖面的数据库,包括各个剖面的采样地点、土壤类型和土壤的理化性质,以及海拔和坡度等地形地貌,年均温和年降水量等生境条件和土地利用类型等信息。由于表层土壤的性质对于外界环境各类变化的响应更为直接,表层SOC含量的变化最明显,由此本文选择表层(A层)SOC作为研究对象。该数据对于采样位置描述缺乏经纬度,但是可以准确到村庄,同时在国家尺度上采用克里格插值等方法,该位置误差对预测精度的影响有限[22]。由此根据土壤剖面位置描述并结合海拔、年均降水量、年均温和年积温等记录进行定位,获取样点数据坐标。去掉无A层土壤有机质数据记录的典型剖面和剔除异常值之后,随机抽取70%的剖面点共1 675个作为建模集,其余30%共718个样点作为验证集,数据样点的空间分布如图1所示。
1.2 环境变量
环境变量的选择主要遵循相关性和可获得原则,即所选环境变量的空间变化能反映土壤属性的空间差异性,而且其易获得并有利于定量化[23]。本文选择气候、植被和地形因子作为辅助SOC预测的环境变量。预选环境变量分别为年均降水量、年均温、≥10℃年积温、高程、坡度、坡向、归一化植被指数(Normalized Difference Vegetation Index,NDVI)、地形位置指数(Topographic Position Index,TPI)、地形粗糙指数(Terrain Ruggedness Index,TRI)以及地形湿度指数(Topographic Wetness Index,TWI)(图2)。
本文的气候数据来自中国农业科学院农业资源与农业区划研究所,是基于全国1915个站点的气象数据,时间区间为建站到1996年。将以上数据经整理和预处理,最后利用反距离加权平均法内插出空间分辨率500m的年均温、年均降水量、≥10℃年积温等栅格数据。NDVI数据来源于“中国西部环境与生态科学数据中心”(http://westdc.westgis. ac.cn),下载GIMMS植被指数数据集并进行投影、掩膜等预处理。全国DEM由来自中国科学院计算机网络信息中心国际科学数据镜像网站(http://www. gscloud.cn)的STRM地形数据拼接而成,利用ArcGIS10.2和SAGA6.3提取和计算坡向、坡度、TPI、TRI以及TWI。
1.3 多元线性回归
MLR是经典的最小二乘法回归模型,能够定量地刻画各个辅助变量对于土壤属性的影响程度,被广泛用于土壤属性的预测和其影响因子的研究中。选用多元逐步线性回归方法,既保证与SOC显著相关的辅助变量进入回归模型又能避免多重共线性[24-25]。利用建模集在SPSS中进行逐步回归模拟,构建SOC与环境变量之间的线性回归模型。

图1 土壤典型剖面点空间分布图
1.4 回归克里格
RK为基于MLR模型得到趋势项与残差项,再用OK对残差进行插值,最后将二者相加得到RK结果。RK不仅综合了自变量对因变量的解释作用,还在一定程度上对随机性变异进行了解释[26]。
1.5 地理加权回归
GWR是一种绘制例如SOC等土壤属性预测图的局部回归方法。GWR是基于将空间位置嵌入回归参数所表示的局部平滑思想,通过局部加权最小二乘法对采样点进行建模[21]。
最佳带宽分配是此方法的关键部分。本文选择了最大似然原则确定的Akaike信息准则(akaike information criterion,AIC)以确定最佳带宽,核类型选择Fixed即固定距离法,用“高斯核”来解决各局部回归分析的空间环境。
1.6 地理加权回归克里格
GWRK模型是对GWR模型的延伸与扩展,其将GWR模型得到的残差采用OK插值,再将残差插值结果与GWR拟合的趋势相加。GWRK充分考虑了空间非平稳性和残差的空间自相关[27]。
1.7 模型验证与评价方法
建模集用于构建不同的SOC预测模型,验证集用于评估不同模型的模拟精度,评价指标包括平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)以及皮尔逊相关系数()。MAE、MRE以及RMSE是预测精度的量度,值越小说明预测方法的结果越精确。
2 结 果
2.1 SOC含量的描述性统计特征及其与环境变量的相关性
如表1所示,SOC含量平均值为22.28 g·kg–1,从1.62 g·kg–1变化至223.88 g·kg–1。SOC含量的变异系数高达96.10%,表明变异幅度极大,为极强的空间异质性。SOC含量的偏度和峰度分别为3.18和15.97,呈正偏态分布特征。将原始SOC数据进行对数转换(lnSOC),转换后偏度和峰度为–0.11和–0.18,Kolmogorov-Smirnov(K-S)检验进一步证明转换后数据符合正态分布特征(>0.05)。
利用所提取的环境变量与SOC进行相关分析。在地形因子中,坡度(0.22)、高程(0.18)、坡向(0.04)以及TRI(0.25)与SOC呈显著正相关(< 0.01),TPI(–0.08)和TWI(–0.09)与SOC呈显著负相关;在气候因子中,年均降水量(0.12)与SOC呈显著正相关,年均温(–0.11)、≥10℃年积温(–0.12)与SOC呈显著负相关;NDVI(0.25)与SOC呈显著正相关。其中NDVI和TRI与SOC相关性最高,坡向与SOC相关性最弱。
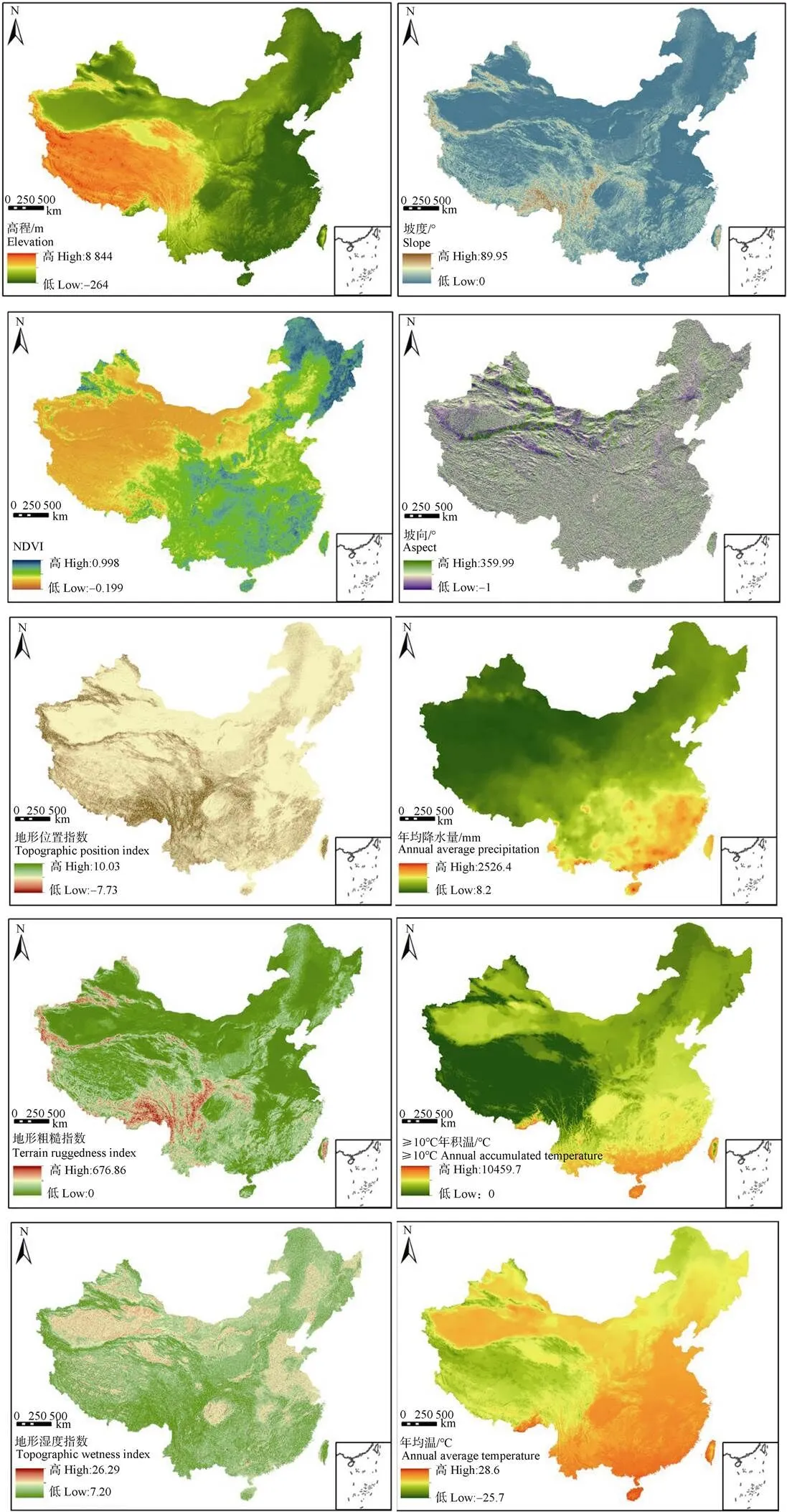
图2 环境变量空间分布图

表1 土壤有机碳含量及其对数转换后的基本描述统计特征
注:SOC:土壤有机碳;lnSOC:对数转换后的土壤有机碳。Note:SOC:soil organic carbon;lnSOC:soil organic carbon after logarithmic transformation.
2.2 GWR和MLR模型构建
由表2可知,最终进入MLR模型的解释变量为高程、年均降水量、年均温、TRI和NDVI,各个解释变量的方差膨胀因子(Variance inflation factor,VIF)均小于7.5,解释变量之间不存在多重共线性现象,值和值表明解释变量与SOC之间存在着显著的相关关系。从标准系数可以看出,模型中各环境变量对SOC影响程度从大到小依次为年均降水量、年均温、NDVI、高程、TRI。MLR模型的决定系数2= 0.186,表示环境变量可以解释SOC含量18.6%的变化。以便对比,选用相同的环境变量应用于GWR模型。
GWR模型的决定系数2= 0.259,表明模型对因变量的解释度可达25.9%,高于MLR。越小的残差平方和表明模型的拟合效果越好。MLR模型的残差平方和为6.25×105,而GWR模型的残差平方和为5.68×105,少于MLR模型。由此可以看出GWR具有较MLR更好的拟合性能。
2.3 SOC含量的空间结构特征
根据Cambardella等[28]对空间自相关性程度的划分,模型的块基比<25%表明所研究的土壤属性具有强烈的空间自相关性;介于25%~75%之间为中等空间自相关性;>75%为弱空间自相关性。OK的半变异函数采用高斯函数进行最优拟合(表3),变程为69.67 m,块金值为0.08,基台值为1.05,块基比为7.62%,说明SOC具有强烈的空间自相关。
残差是SOC含量测量值与模型预测值之间的差异。将GWR和MLR预测所得的残差进行OK插值,分别得到它们的残差空间分布图(图3)。由表3所示,MLR和GWR残差拟合的半变异函数均为高斯模型,两者块基比分别为9.52%和10.56%,表明均有强烈的空间自相关性,前者空间自相关性较后者强,再通过交叉验证中GWR残差的均方根小于MLR残差,其平均值也更接近于0,均表明GWR较MLR具有更高的精度。MLR拟合后的残差范围由图3可知,残差负值主要分布在中西部,表明预测值高于观测值;正值主要分布在东北部和西南部,表明预测值低于观测值。GWR残差的空间分布模式与MLR残差类似。但是,两者也存在细微差异。GWR残差的最小值和最大值分别为–42.26 g·kg–1和184.08 g·kg–1,而MLR残差范围为–42.55 g·kg–1~183.81 g·kg–1,同时GWR模型残差在极值范围的图斑面积均小于MLR残差。
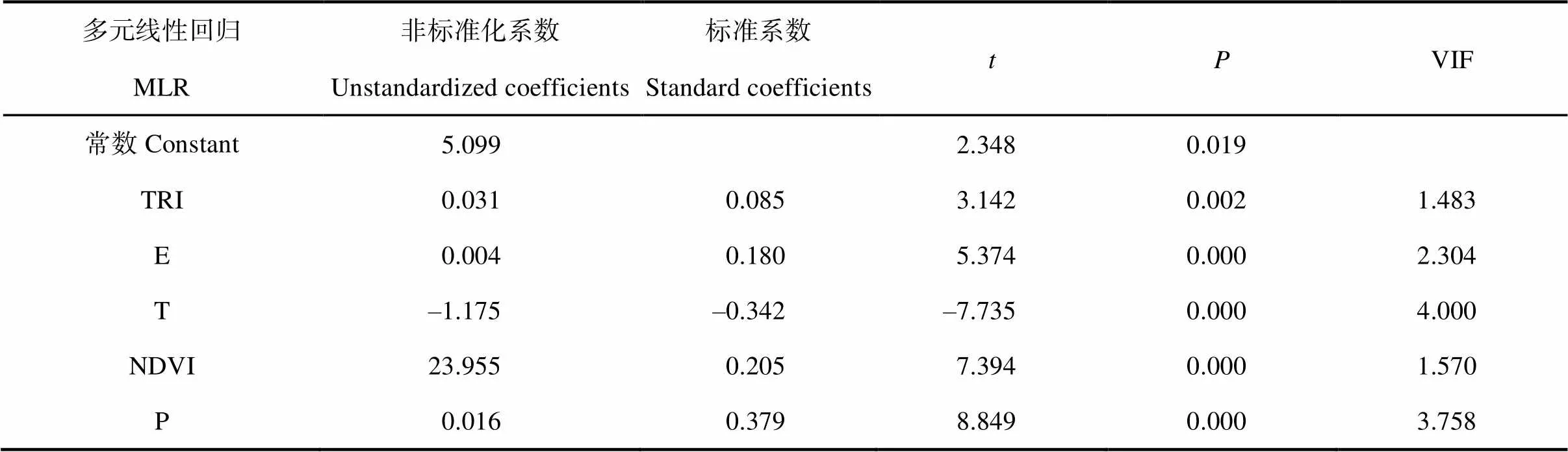
表2 多元线性回归模型系数的基本统计特征

表3 GWR、MLR残差及SOC的半方差函数参数
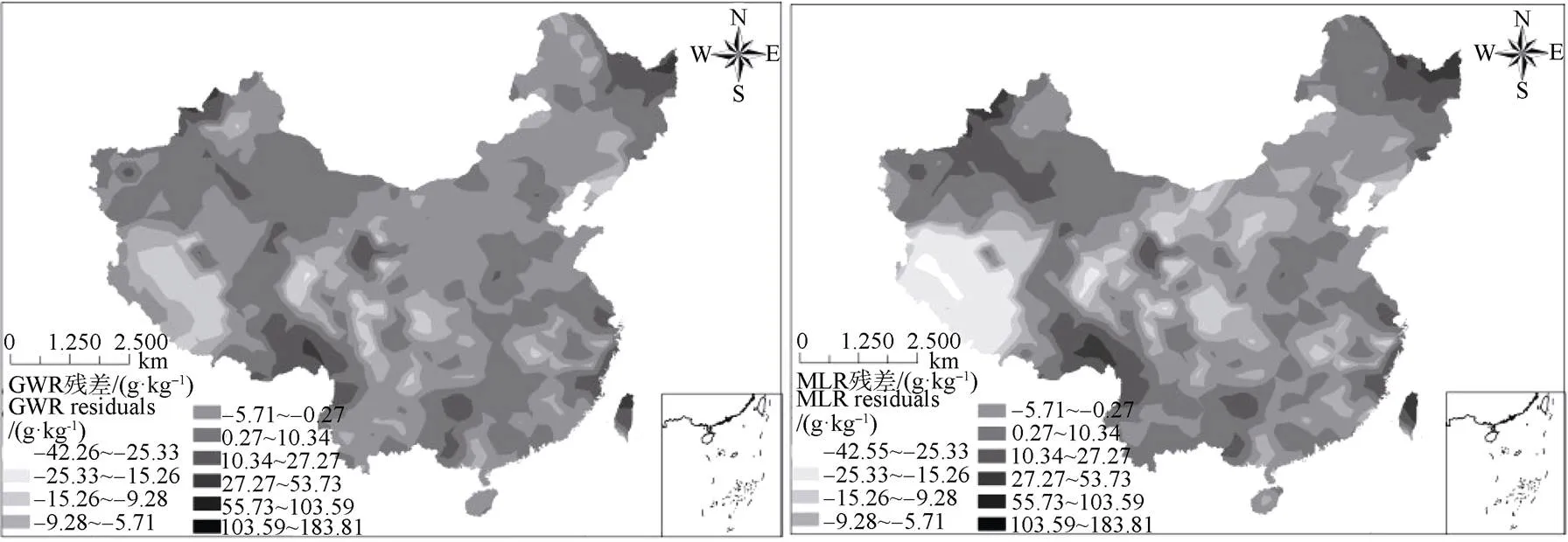
图3 GWR和MLR土壤有机碳残差的空间分布
2.4 不同模型预测精度比较
基于验证集,以OK为对照,利用MAE、MRE、RMSE和来评估模型的模拟精度,结果如表4所示。验证结果表明,GWR的MRE、MAE和RMSE值最小,值最高,因此GWR模型的预测精度最高。GWRK的MRE、MAE和RMSE值分别为0.850、12.336和19.035,仅大于GWR模型,值为0.460仅小于GWR模型,表明其预测精度只低于GWR。五种模型中,OK的MRE、MAE和RMSE均高于其余模型,值低于其余模型,精度最低。
2.5 SOC的空间分布特征
图4是基于OK、MLR、RK、GWR、GWRK五种模型得到的中国SOC空间分布预测专题图。从研究区域的空间结构和变化趋势来看,五幅分布图在整体上表现出相似的SOC空间分布特征,同时在局部地区又表现出一定的差异性。从整体分布来看,SOC的空间分布具有明显的带状结构特征。SOC含量较高值分布在研究区东北部的平原、西南部以及东南部的离散地区,而西北部SOC含量普遍偏低。在局部细节上,五幅分布图存在着明显的差异性。GWR和GWRK预测得到的SOC含量范围大于MLR和RK,前者更能反映SOC的真实情况。对于SOC含量较高值分布的区域,较GWR和MLR相比,RK和GWRK模型预测的图斑面积明显较大。在东北部MLR模型预测的SOC含量普遍低于其余四个模型。这主要是由于OK仅考虑了土壤采样点的空间自相关性,MLR忽略了辅助变量的空间自相关性,GWR同时考虑了土壤采样点和辅助变量的空间异质性,而RK和GWRK不仅考虑了区域环境变量的空间变异性,还考虑了GWR和MLR的残差。通过RK和GWRK分布图可以发现,研究区西部的高原与沙漠地区出现突变情况,主要原因在于这些地区因采样难度大且数据缺乏,残差插值效果不佳。
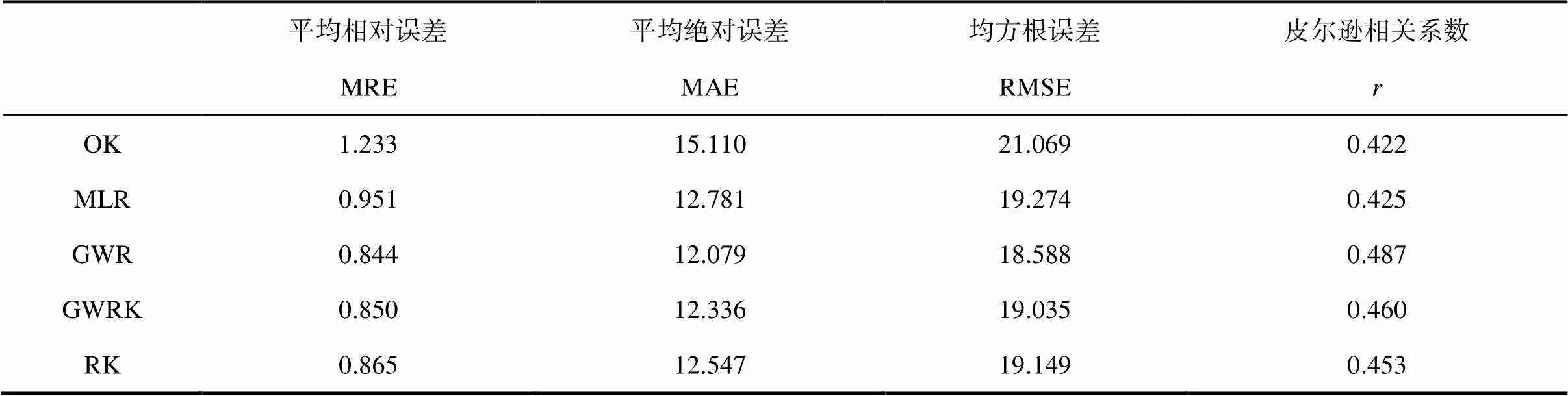
表4 OK、MLR、GWR、GWRK、RK五种模型的精度评价指标比较
3 讨 论
3.1 环境变量与SOC之间的空间非平稳性
本文选用地形、气候和植被因子作为环境变量应用于GWR模型。不同环境变量回归系数的空间分布如图5所示,不同环境变量对SOC的影响在不同地理位置上可能有所不同。其中具有最大绝对系数值的是NDVI,其次是年均温和TRI。NDVI与SOC在中部和东部地区呈负相关,西部呈正相关,NDVI对SOC的影响由西部向东南部递减。NDVI直接反映植被生长状况的优劣,而植被是SOC的重要来源之一[29],影响着SOC储量及其动态平衡[30],同时良好的地表覆盖还能减少侵蚀的发生,防止SOC流失。年均温与SOC在西北部和中部呈正相关,其余区域呈负相关,这可能是因为较低的温度更利于SOC的积累。气候影响植被的分布和生长,同时也是制约凋落物分解的主要因素,与SOC输入和分解紧密相关。温度主要通过提高净初级生产力以增加输入土壤中的凋落物数量,提高SOC含量和通过促进微生物活动、土壤呼吸从而加速SOC分解、增加SOC分解量两方面来影响SOC[31]。TRI与SOC在西北部盆地区域呈正相关,其余区域呈负相关。土壤属性的空间变异受多种因子的控制,而地形作为五大成土因素中的重要因素,能调节热量和物质的再分配[32-33],对SOC分布起重要作用[34-35]。其余环境变量系数表明其对SOC空间变化的影响较弱。截距是回归模型的常数项,范围为–31.18~48.42。尽管回归系数在一定程度上体现了对应环境因素对SOC的影响,但是在大尺度上气候、植被以及地形因素在时间和空间上是复杂多变且相互作用的,再加上样点在沙漠和高原地区数据稀少和整体分布不均等样本局限性,SOC空间分布的不确定性仍然存在。
3.2 SOC预测精度差异性对比
本文以OK模型为对照,使用GWR、MLR、RK和GWRK模型结合地形、植被和气候因子预测中国SOC含量的空间分布,结果表明GWR是相对合适的模型。GWR技术包含权重函数的MLR变体,不仅考虑了SOC的空间异质性和变异性,还考虑了环境变量之间的关系[24]。GWR被发现是用于宏观地理土壤研究的优秀工具[19]。Wang等[36]对比了GWR和MLR在土壤有机质空间预测方面的差异,认为GWR能更准确地预测土壤有机质的空间分布和更多细节。文中GWR下的SOC空间分布图也较MLR更加精细。Zhang等[14]调查了GWR方法在爱尔兰模拟SOC空间分布中的应用,认为GWR减小了空间插值的平滑效果,为SOC分布图提供了一种很有前途的方法。OK直接利用建模样本进行插值,虽然充分利用样点自身结构特征,但其并未考虑与SOC变化密切相关的环境变量。MLR是通过对实测数据的统计分析来建模,数据量和数据精度均制约着预测精度。李启权等[37]将MLR与HASM相结合的方法与OK比较,证明前者在模拟中国土壤有机质空间分布上相对有效。RK基于SOC与环境变量之间的关系建立全局回归模型,还能利用样点的空间自相关性进行OK插值,综合考虑了结构性与随机性[24]。Mishra和Riley[38]比较了简单平均法和RK估计美国中西部SOC储量的预测精度,发现RK能更准确地反映SOC储量的异质性。GWRK是一种混合技术,通过充分考虑空间参数非平稳性以及SOC与其他环境变量之间的关系,从而获得GWR的优点[21-39],其残差也可以通过OK插值作为空间随机的一部分添加到估计的趋势中[27]。Kumar等[27]采用GWRK模型研究美国宾夕法尼亚州的环境变量与SOC之间的关系,证明了GWRK在捕捉空间非平稳性方面的优越性。


图5 GWR模型中环境变量系数的空间分布
本文研究区为国家尺度,范围广但样点分布并不能保证均一性,特别是研究区西部的样点相对于其他区域数量少且分布稀疏,再加上样本数据和残差的空间自相关,导致OK插值出来的残差分布并不能真实反映SOC预测之后的残差分布,由此,RK和GWRK预测的SOC结果在某些样本数据少的区域效果不佳,从而严重影响了RK和GWRK的预测精度以及SOC的空间分布。同时实际采样点坐标与本文所匹配的样点位置存在误差,这也是不确定性的来源。定量化研究环境变量与SOC之间的关系,环境变量的获取非常关键。获取环境变量需要广泛应用DEM,而且其精度和空间分辨率均影响最终的分析结果[33],如果使用更高分辨率的DEM和进一步研究更为详尽的环境变量则更多残差可能会被解释。然后在充分分析SOC与环境变量作用机理的基础上,选择合适的方法估计SOC含量的空间分布,预测效果将进一步提高。
4 结 论
本文共使用了五种模型来估计SOC含量的空间分布,以地形因子(高程和TRI)、气候因子(年均降水量和年均温)和植被指数(NDVI)作为辅助变量,比较OK、MLR、RK、GWR和GWRK模型的建模结果。研究结果表明:(1)SOC及其环境变量在全国尺度上有很强的变异性,在研究区域内存在显著差异性;(2)SOC与高程、TRI、NDVI、年均降水量以及年均温呈极显著相关关系;(3)在全国尺度上,较高SOC含量主要分布在东北部、西南部以及东南部区域,而西北部SOC含量普遍偏低;(4)GWR模型具有较好的拟合精度,预测结果优于OK、MLR、RK和GWRK模型。
[1] Davidson E A,Trumbore S E,Amundson R. Biogeochemistry-soil warming and organic carbon content. Nature,2000,408(6814):789—790.
[2] Zhao M S,Li D C,Wang S H. Variation of Soil Organic Carbon in Farmland of Anhui and Its Influencing Factors in The 30 Years from 1980 to 2010. Acta Pedologica Sinica,2018,55(3):595—605. [赵明松,李德成,王世航. 近30年安徽省耕地土壤有机碳变化及影响因素. 土壤学报,2018,55(3):595—605.]
[3] Eswaran H,Vandenberg E,Reich P. Organic-carbon in soils of the world. Soil Science Society of America Journal,1993,57(1):192—194.
[4] Batjes N H. Total carbon and nitrogen in the soils of the world. European Journal of Soil Science,1996,47(2):151—163.
[5] Bohn H L. Estimate of organic-carbon in world soils. Soil Science Society of America Journal,1982,46(5):1118—1119.
[6] Post W M,Emanuel W R,Zinke P J,et al. Soil carbon pools and world life zones. Nature,1982,298(5870):156—159.
[7] Schlesinger W. Carbon storage in the caliche of arid soils:A case study from arizona. Soil Science,1982,133(4):247—255.
[8] Dai W,Huang Y. Relation of soil organic matter concentration to climate and altitude in zonal soils of china. Catena,2006,65(1):87—94.
[9] Thompson J A,Kolka R K. Soil carbon storage estimation in a forested watershed using quantitative soil-landscape modeling. Soil Science Society of America Journal,2005,69(4):1086—1093.
[10] Xie X L. Study on soil organic carbon stocks in national and regional scale using GIS. Nanjing:Nanjing Normal University,2004. [解宪丽. 基于GIS的国家尺度和区域尺度土壤有机碳库研究,南京:南京师范大学,2004.]
[11] Setia R,Smith P,Marschner P,et al. Introducing a decomposition rate modifier in the rothamsted carbon model to predict soil organic carbon stocks in saline soils. Environmental Science & Technology,2011,45(15):6396—6403.
[12] Liu F,Rossiter D G,Song X D,et al. A similarity-based method for three-dimensional prediction of soil organic matter concentration. Geoderma,2016,263:254—263.
[13] Wang S H,Shi X Z,Zhao Y C,et al. Regional simulation of soil organic carbon dynamics for dry farmland in east china by coupling a 1:500 000 soil database with the century model. Pedosphere,2011,21(3):277—287.
[14] Zhang C S,Tang Y,Xu X L,et al. Towards spatial geochemical modelling:Use of geographically weighted regression for mapping soil organic carbon contents in ireland. Applied Geochemistry,2011,26(7):1239—1248.
[15] Kumar S. Estimating spatial distribution of soil organic carbon for the midwestern united states using historical database. Chemosphere,2015,127:49—57.
[16] Zhao Y C,Shi X Z,Yu D S,et al. Different methods for prediction of spatial patterns of soil organic carbon density in HeBei province,China. Acta Pedologica Sinica,2005,42(3):379—385. [赵永存,史学正,于东升,等. 不同方法预测河北省土壤有机碳密度空间分布特征的研究. 土壤学报,2005,42(3):379—385.]
[17] Watt M S,Palmer D J. Use of regression kriging to develop a carbon:Nitrogen ratio surface for new zealand. Geoderma,2012,183:49—57.
[18] Brunsdon C,Fotheringham S,Charlton M. Geographically weighted regression - modelling spatial non-stationarity. Journal of the Royal Statistical Society Series D-the Statistician,1998,47:431—443.
[19] Scull P. A top-down approach to the state factor paradigm for use in macroscale soil analysis. Annals of the Association of American Geographers,2010,100(1):1—12.
[20] Harris P,Fotheringham A S,Crespo R,et al. The use of geographically weighted regression for spatial prediction:An evaluation of models using simulated data sets. Mathematical Geosciences,2010,42(6):657—680.
[21] Liu Y,Guo L,Jiang Q,et al. Comparing geospatial techniques to predict soc stocks. Soil & Tillage Research,2015,148:46—58.
[22] Zhao Y C,Xu X H,Hai N,et al. Uncertainty assessment for mapping changes in soil organic matter using sparse legacy soil data and dense new-measured data in a typical black soil region of china. Environmental Earth Sciences,2015,73(1):197—207.
[23] Yang S H. Study on the regional distribution of soil organic matter based on spatial regression model.Wuhan:Huazhong Agricultural University,2016. [杨顺华. 基于空间回归模型的土壤有机质区域分布特征研究,武汉:华中农业大学,2016.]
[24] Yang S H,Zhang H T,Guo L,et al. Spatial interpolation of soil organic matter using regression Kriging and geographically weighted regression Kriging. Chinese Journal of Applied Ecology,2015,26(6):1649—1656. [杨顺华,张海涛,郭龙,等. 基于回归和地理加权回归kriging的土壤有机质空间插值.应用生态学报,2015,26(6):1649—1656.]
[25] Zhang G P,Guo P T,Wang Z Y,et al. Prediction of spatial distribution of soil nutrients in farmland in purple soil hilly region. Transactions of the CSAE,2013,29(6):113—120. [张国平,郭澎涛,王正银,等. 紫色土丘陵地区农田土壤养分空间分布预测. 农业工程学报,2013,29(6):113—120.]
[26] Jiang Y F,Sun K,Guo X,et al. Prediction of spatial distribution of soil properties based on environmental factors and neighboring information. Research of Environmental Sciences,2017,30(7):1059—1068. [江叶枫,孙凯,郭熙,等. 基于环境因子和邻近信息的土壤属性空间分布预测. 环境科学研究,2017,30(7):1059—1068.]
[27] Kumar S,Lal R,Liu D. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geofisica Internacional,2012,189—190(6):627—634.
[28] Cambardella C A. Field-scale variability of soil properties in central iowa soils. Soilence Society of America Journal,1994,58(5):1501—1511.
[29] Li L,Yao Y F,Qin F C,et al. Analysis of factors affecting soil organic carbon density based on geographically weighted regression model. Science & Technology Review,2016,34(2):247—254. [李龙,姚云峰,秦富仓,等. 基于地理加权回归模型的土壤有机碳密度影响因子分析. 科技导报,2016,34(2):247—254.]
[30] Jarvis P,Rey A,Petsikos C,et al. Drying and wetting of mediterranean soils stimulates decomposition and carbon dioxide emission:The“birch effect”. Tree Physiology,2007,27(7):929—940
[31] Trumbore S E,Chadwick O A,Amundson R. Rapid exchange between soil carbon and atmospheric carbon dioxide driven by temperature change. Science,1996,272(5260):393—396.
[32] Liu F,Zhang G L,Sun Y J,et al. Mapping the three-dimensional distribution of soil organic matter across a subtropical hilly landscape. Soil Science Society of America Journal,2013,77(4):1241—1253.
[33] Lian G,Guo X D,Fu B J,et al. Prediction of the spatial distribution of soil properties based on environmental correlation and geostatistics. Transactions of the Chinese Society of Agricultural Engineering,2009,25(7):237—242. [连纲,郭旭东,傅伯杰,等. 基于环境相关法和地统计学的土壤属性空间分布预测. 农业工程学报,2009,25(7):237—242.]
[34] Bennie J,Huntley B,Wiltshire A,et al. Slope,aspect and climate:Spatially explicit and implicit models of topographic microclimate in chalk grassland. Ecological Modelling,2008,216(1):47—59.
[35] Wang L,Wang Q,Wei S,et al. Soil desiccation for loess soils on natural and regrown areas. Forest Ecology & Management,2008,255(7):2467—2477.
[36]Wang K,Zhang C R,Li W D,et al. Mapping soil organic matter with limited sample data using geographically weighted regression. Surveyor,2014,59(1):91—106.
[37] Li Q Q,Yue T X,Fan Z M,et al. Study on method for spatial simulation of topsoil SOM at national scale in China. Journal of Natural Resources,2010,25(8):1385—1399. [李启权,岳天祥,范泽孟,等. 中国表层土壤有机质空间分布模拟分析方法研究. 自然资源学报,2010,25(8):1385—1399.]
[38] Mishra U,Riley W J. Alaskan soil carbon stocks:Spatial variability and dependence on environmental factors. Biogeosciences,2012,9(9):3637—3645.
[39] Du P Y,Zhang H T,Guo L,et al. Variation of Soil Organic Matter in Transition Zones and Its Influencing Factors. Acta Pedologica Sinica,2018,55(5):1286—1295. [杜佩颖,张海涛,郭龙,等. 平原丘陵过渡区土壤有机质空间变异及其影响因素. 土壤学报,2018,55(5):1286—1295.]
Characterization of Spatial Distribution of Soil Organic Carbon in China Based on Environmental Variables
LUO Mei, GUO Long†,ZHANG Haitao, WANG Shanqin, LIANG Pan
(College of Resource and Environment, Huazhong Agricultural University, Wuhan 430070, China)
Soil organic carbon content in China and its variation plays a very important role in the global carbon cycle and variation of atmospheric carbon dioxide concentration. The processes of soil formation, development and erosion are subject to impacts of the complex and volatile environmental factors in the surroundings of the soil, so soil organic carbon is of strong spatial variability and dependence.Based on the data of soil organic carbon contents in the surface layers of 2 473 soil profiles collected during the Second National Soil Survey, this paper explored influences of factors, like topography, vegetation and climate on spatial distribution of soil organic carbon; With the ordinary Kriging method as control, geographically weighted regression, geographically weighted regression Kriging, multiple linear regression and regression Kriging were used separately to modeling for spatial prediction of soil organic carbon; indices, like mean absolute estimation error (MAE), mean relative error (MRE), root mean square error (RMSE) and Pearson correlation coefficient(r)were used to evaluate performance of these models; and soil organic carbon spatial distribution prediction maps were drawn separately.Results show: (1) Soil organic carbon varied in the range from 1.62 g·kg–1to 223.88 g·kg–1in content and averaged to be 22.28 g·kg–1in the country. Its variation coefficient reached 96.10%, which indicates that organic carbon in the soil varies very sharply in range, and is of strong spatial heterogeneity; (2) Soil organic carbon content was significantly related to annual mean precipitation, ≥10℃annual accumulated temperature, elevation, slope, aspect, normalized difference vegetation index, annual average temperature, topographic wetness index, topographic position index and topographic roughness index. Among them, slope, elevation, aspect, topographic roughness index, annual average precipitation and normalized vegetation index were positively related, while topographic position index, topographic wetness index, annual average temperature and ≥10℃accumulated temperature were negatively related; (3) Multiple linear regression coefficients might reflect influences of the environmental variables on soil organic carbon globally, whereas the geographically weighted regression coefficient map might do clearly those of different environmental variables on soil organic carbon in different geographical locations; (4) The mean absolute estimation error, root mean square error, mean relative error and Pearson correlation coefficient of the model were used as model validation indices and indicated that the geographically weighted regression is higher than the other models in prediction accuracy, and hence can be used to plot soil organic carbon spatial distribution characteristics maps of large scales areas; and (5) Areas relatively high in soil organic carbon content were mainly distributed in the northeast and southwest of the studied region, and patches in the southeast, while areas relatively low were in the northwest.The geographically weighted regression is higher than the ordinary Kriging, multiple linear regression, regression Kriging and geographically weighted regression Kriging in prediction accuracy. In this paper, efforts have been made to explore correlations between soil properties and environmental variables on large scales in an attempt to provide certain solutions and ideas for soil properties spatial mapping.
Soil organic carbon; Environmental variable; Geographically weighted regression; Multiple linear regression
S159.2
A
10.11766/trxb201812110454
罗梅,郭龙,张海涛,汪善勤,梁攀. 基于环境变量的中国土壤有机碳空间分布特征[J]. 土壤学报,2020,57(1):48–59.
LUO Mei,GUO Long,ZHANG Haitao,WANG Shanqin,LIANG Pan. Characterization of Spatial Distribution of Soil Organic Carbon in China Based on Environmental Variables[J]. Acta Pedologica Sinica,2020,57(1):48–59.
* 湖北省自然科学基金项目(2018CFB372)、中国科学院水生植物与流域生态重点实验室开放课题(Y852721s04)和国家自然科学基金项目(41471179)资助Supported by the Hubei Provincial Natural Science Foundation of China(No. 2018CFB372),Open Funding Project of the Key Laboratory of Aquatic Botany and Watershed Ecology,Chinese Academy of Sciences(No. Y852721s04)and the National Natural Science Foundation of China(No. 41471179)
,E-mail:guolong@mail.hzau.edu.cn
罗 梅(1996—),女,重庆永川人,硕士研究生,主要从事数字土壤制图方面的研究。E-mail:luomei@webmail.hzau.edu.cn
2018–12–11;
2019–03–21;
2019–05–07
(责任编辑:檀满枝)

