有效块的多特征融合的目标跟踪方法

刘晓栋，尚振宏，黄 欢

昆明理工大学 信息工程与自动化学院，昆明650500

1 引言

目标跟踪是计算机视觉领域的一个热点，被广泛应用于视频监控、机器人学习、工业智能化等方面。其本质是在一段连续视频序列图像中找到目标的位置和状态[1]。虽然目前目标跟踪已经取得很大进展，但因受到遮挡、光照变化和尺度变化等众多因素影响，它仍然是一个具有挑战性的问题。

目前大多数目标跟踪方法通常使用边界框表示被跟踪目标的范围。但是大多数被跟踪目标都不是严格意义上的矩形形状，因此边界框表示跟踪目标时，通常都会把多余的背景信息加入到模型中，背景信息过多的情况下可能会降低跟踪器的整体性能。因此，矩形边界框并非表示非矩形形状目标的最佳方式。现在的跟踪技术为了更准确地进行跟踪目标中的形状，已经探索出基于分割方法[2-3]为无模型目标建立准确的方法。尽管视频分割技术[4]已经在视频目标跟踪中有了很大的进展，但是基于分割的方法处理杂乱的背景和遮挡也很具有挑战性，这通常会导致不稳定的结果。

另一类对遮挡和变形比较稳健的跟踪方法是基于目标关键点的跟踪方法[5-6]，它们通过一组显著点（如SIFT特征或SURF特征）表示目标对象[7]。然而，基于关键点的跟踪方法很难仅通过使用局部点获取跟踪目标的全局信息，特别是对于跟踪目标和背景信息同质的情况下。

目前随着深度学习的兴起，一种结构推理网络的理论被应用于运动目标的跟踪，这种方法将物体检测问题形式化为图结构推理，采用细节特征、场景上下文、以及物体之间关系的图结构，采用循环单元的消息传递机制对目标进行联合推理，不过综合性能取决于数据模型的大小[8]。

与使用整体特征表示的跟踪方法相比，结构化的跟踪方法通常更有前途，特别是在变形和遮挡的情况下[9]，并且被跟踪目标在发生遮挡时，单独使用HOG特征的跟踪算法，容易发生漂移，即HOG特征不能很好处理遮挡问题；而当目标发生剧烈光照变化时，颜色直方图特征[10]不能很好处理光照变化问题。实验表明，HOG特征对光照变化具有较好适应性，颜色直方图特征对目标形变、尺度变化具有较好适应性。

因此，在本文中把被跟踪目标表示成为一组块粒子，利用置信度判断哪些块是有效的，通过投票确认目标最终位置。并基于基础跟踪方法单一特征提取的不足，利用HOG特征和颜色直方图特征线性融合的方法提高跟踪方法的鲁棒性和精度。

2 序列蒙特卡罗方法

在识别和跟踪目标对象时，用一组块粒子表示目标对象，由于刚开始很难找到确切可靠的块，利用序列蒙特卡罗[11]方法实现在先验条件不足的情况下对目标状态的估计。

首先，从边界框中取一个样本图像块x=[x,y,w,h]，其中( x,y)( w,h)分别代表图像样本x的坐标和大小。xt代表图像样本中的块粒子，zt是基于跟踪目标先前帧z1:t-1=中的观察值，从贝叶斯理论看，状态估计问题比如目标跟踪方面，就是根据之前一系列已有数据z1:t-1，递推计算出当前状态xt的可信度，那么这个可信度就是概率公式，然后通过预测和更新两个步骤递推计算，假设已知t-1时刻的概率密度函数为p( xt-1|z1:t-1)。那么在预测时，由上一时刻的概率密度p( xt-1|z1:t-1)就可以得到p( xt|z1:t-1) ，p( xt|z1:t-1)的含义是有前面(1:t-1)时刻测量数据，那么就可以预测一下状态xt出现概率。因此可以把当前帧zt中块粒子xt是否可靠的概率密度函数表示为：

其中p( xtz1:t-1)为概率密度函数，根据贝叶斯公式规|则，式（1）在进行更新时由p( xt|z1:t-1)得到后验概率p( xt|z1:t)，这里的后验概率p( xt|z1:t)也将利用式（1）代入到下次预测，形成预测、更新、再预测的递推关系。因此后验概率p( xt|z1:t)可以被表示为：

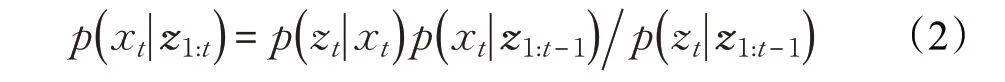
其中的p( zt|xt)为观测似然值，p( xt|xt-1)表示为过渡密度函数，是一个一阶马尔科夫模型，也就是说xt的状态只与上一时刻的xt-1有关，选取G作为高斯分布，那么p( xt|xt-1)就可以被表示为：

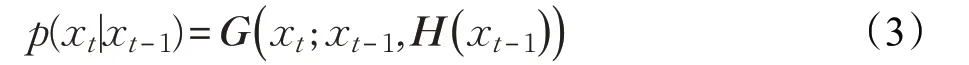
其中H(x)=[0 ,E] x是一个选择图像坐标的函数，E代表的是一个2×2的单位矩阵，那么可观测的似然值p( zt|xt)就可以被表示为：

其中pt( zt|xt)表示有效跟踪块的置信度，而po( zt|xt)表示块在被跟踪对象上的可能值。由于变量x数据太大而无法直接计算，采用粒子滤波器[2]估计后验p( xt|z1:t-1)的值，那么第i个块粒子权重就可以通过式（5）计算：

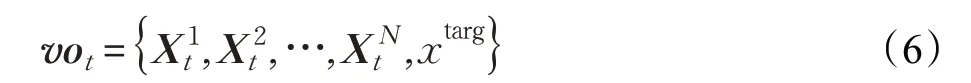
其中xtarg代表的是最终的目标跟踪状态。

2.1 可跟踪块的观察似然值

要估计块的有效跟踪的可能性，采用Peak-to-Sidelobe Ratio（PSR）作为置信度[12]，这种方法广泛用于信号处理，以测量响应图中的信号峰值强度。在文献[12]中采用PSR作为跟踪目标的峰值强度，基于此，将PSR推广到基于模板的跟踪器，作为块跟踪的置信度函数，判断块粒子是否对跟踪起积极的作用：

其中R(X)是图像块的响应函数，以R(X)峰值为中心，15×15像素为边界框对R( )

X划分区域，边界框以外的为旁瓣区域Φ，μΦ和σΦ分别表示旁瓣区域Φ的均值和标准差，从式（7）可以看出，响应函数R()X的峰值越大，s( X )就会越大，因此s( X)可以作为图像块的置信函数，用来衡量图像块是否对跟踪起积极作用。当s(X )大于0时，则标记块粒子为积极的。响应函数R(X)可以被表示成：

其中d表示模板T和图像块X之间的欧氏距离，f(X)表示图像特征提取函数。由于响应函数R()X与模板T和采样图像块之间的距离成反比，所以块跟踪置信度函数s()

X值越大，样板T和图像块X之间的距离越近，反之亦然。

而且块跟踪置信度函数s( )X与大多数基础跟踪方法兼容，因为大多数相关滤波跟踪方法采用最大响应图作为被跟踪目标的位置，并且都有一个基础模板，所以采用基于核相关和循环矩阵而取得高效率和高速度的KCF[13]作为基础跟踪方法，并基于KCF单独的HOG特征在发生强烈光照变化和形变时，会发生严重漂移问题，而颜色直方图对形变和颜色变化比较敏感，所以融合两种特征的KCF可以获得更好精度的响应图。

在KCF中，循环位移产生的样本能够近似的表示通过密集采样所产生的样本，假如有一维数据x=[x1,x2,…,xn]，那么一维数据x的循环移位Px=[xn,x1,x2,…,xn-1]T，{Pux|u=0,1,…,n-1}中u代表移位的个数，在这个式子中每乘一次P，则代表着x中的元素就循环偏移一位，因此所有的循环样本被链接起来形成一个矩阵X=C()x，把X称为循环矩阵，并且把循环矩阵表示为：

其中，F代表的是离散傅里叶变换（DFT），FH是F的共轭转置矩阵，x^代表对x进行离散傅里叶变换，diag表示向量对角化。在KCF中循环矩阵的分解可用于简化线性回归的解，线性脊岭回归的目标函数可以被表示为：

函数f可以写成基础样本的线性组合f(x)=ωTy，脊岭回归具有完全封闭的解ω=( XTX+λI)-1XTy，由式（9），可以得到：

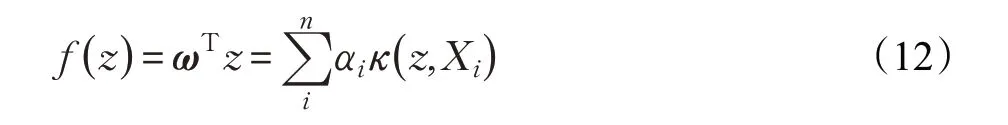
因此对于上式的核函数，也可以使用KCF中循环矩阵技巧。因此，KXX表示循环矩阵的第一行向量，通过上面的方法可以得到α，相当于线性回归方程中的ω。

在KCF中利用循环矩阵技巧的高斯核被表示为：

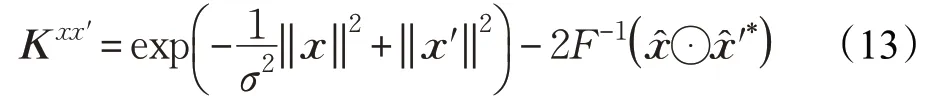
由上式可知由于核相关函数只需要计算点乘积和矢量范数，使计算量大大减少，因此把图像特征被应用到多个通道，多个通道特征数据也可以连接成一个一维向量，式（13）可以被表示为：

在式（14）特征数据也链接成为一维之后，KCF不仅仅可以使用HOG特征，也可以利用到其他优秀的特征，所以可以通过式（14）进行HOG特征和颜色特征线性融合并利用它们的优势。

之后，采用基于多特征线性融合后的KCF响应图促进跟踪置信度函数s( )X。因此，可跟踪块粒子观测值可以表述如下：

其中λ是用于权衡可能性贡献系数。在本文中经过多次实验，设定λ=2时，实验效果最好。

2.2 在目标上的跟踪块观察似然值

为计算位于被跟踪物体上的有效块的概率，利用运动信息实现这一目标。具体来说，跟踪前景和背景块粒子，并记录每一个块的相对轨迹：

其中的vt=ψ2( )xt-xt-1是相对运动矢量。由于块粒子的位移可能对应于不同的物体，记录k个相对运动矢量以使轨迹信息更加稳定。使用L2范数公式测量轨迹之间的距离。并对轨迹进行分组，以一个矩形框目标为中心简单地将图像分成两个区域。然后，将边界框上和边界框内的块粒子标记为正，而将外部的块粒子标记为负：

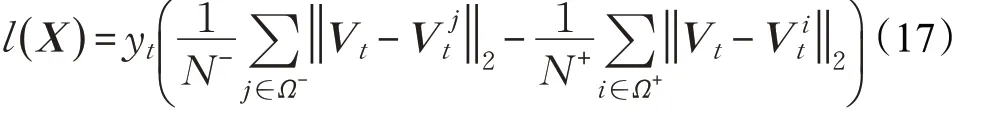
其中yt∈{+ 1,-1}代表的是图像块Xi的标签，Ω+代表的是积极块粒子的集合，Ω-代表的是消极块粒子的集合。N+和N-分别表示为积极响应集和消极响应集的大小。当一组样本块粒子有相同运动时，函数l(X)具有较高的分数值，反之分数值就会很低，当每组之间的运动轨迹没有明显的距离时，该函数的值接近于零。因此，可以在块粒子集中标记每个块粒子，将重点集中在那些在目标对象上的块粒子。因此，使用l(X)计算块粒子在目标对象上的概率：

其中μ是平衡对象概率贡献的系数，本文中值为1。如果前景和背景之间没有明显的运动变化，po趋近于1。

2.3 基于投票的最佳位置估计

在pt( zt|xt)和po( zt|xt)的结果被计算之后，假设可靠的块在结构上与被跟踪物体一致，可以将粒子的权重作为被跟踪目标块的置信度量度值。那么，使用所有积极块粒子投票到目标最终的位置，如下所示：

3 算法流程

3.1 粒子重采样

运动目标跟踪的过程中，一组块粒子经过一段时间的运算，效果会越来越差，称这种情况为块粒子的退化[14]，本文采用SIR方法对粒子进行重采样，详细方法可以参考文献[14]。

3.2 算法具体步骤

输入：模型vot-1和新的一帧图片It。

（1）对于在目标模型vot-1中每一个块粒子，在新的一帧中用基于多特征融合后的基础跟踪方法KCF做跟踪，以获取最大响应图。

（2）在Xit中更新xit和Vit。

（3）根据式（5）计算粒子重量ω。

（4）块粒子重采样。

（6）根据式（6）更新模型vot。

输出：更新的模型vot用于目标跟踪；得到新目标状态

4 实验结果与分析

4.1 实验环境及参数

本次实验中所使用到的工具有：Matlab2015 Athlon（速龙）X2 CPU（2.10 GHz）4 GB RAM，λ=2,μ=1。

4.2 数据集和评估方法

实验选取公开的标准测试数据集Benchmark[15]中12段视频序列进行实验，测试视频序列依次为BlurBody、BlurFace、Boy、CarDark、Coke、David3、Deer、Girl、tiger2、Vase、BlurCar2和Box，其中包含了目标多种变化，如遮挡、快速运动和旋转、光照变化、尺度变化等影响因素的12个视频序列上，进行跟踪实验，并与7种优秀方法进行比较，这7种目标跟踪方法分别是Conv_KCF[16]、CSK[17]、RPT[18]、DFT[19]、DSST[20]、IVT[21]、KCF。

本文采用平均跟踪误差Center Location Error（CLE）和重叠率Pascal VOC Overlap Ratio（VOR）来评估本文算法和其他比较算法。

CLE是指目标框的中心与目标真实位置中心之间的偏差。中心误差越小，则算法性能越高。VOR中BC和BG分别表示跟踪框的实际大小和真值。重叠率越高，则算法性能越高。平均跟踪误差和重叠率结果如表1和表2，时间效率结果如表3。

其他算法的对比图，如图1所示。

表1 平均跟踪误差

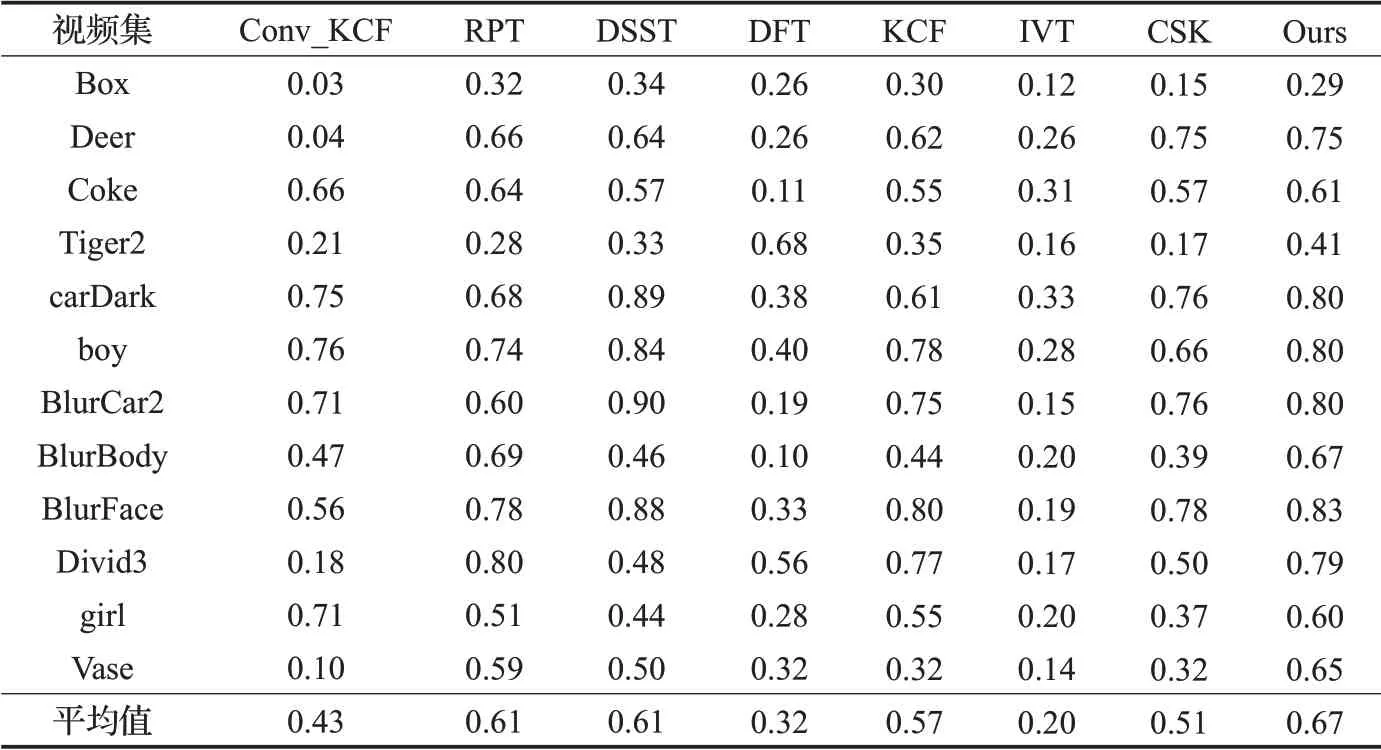
表2 重叠率

表3 不同算法的时间效率 （帧·s-1）

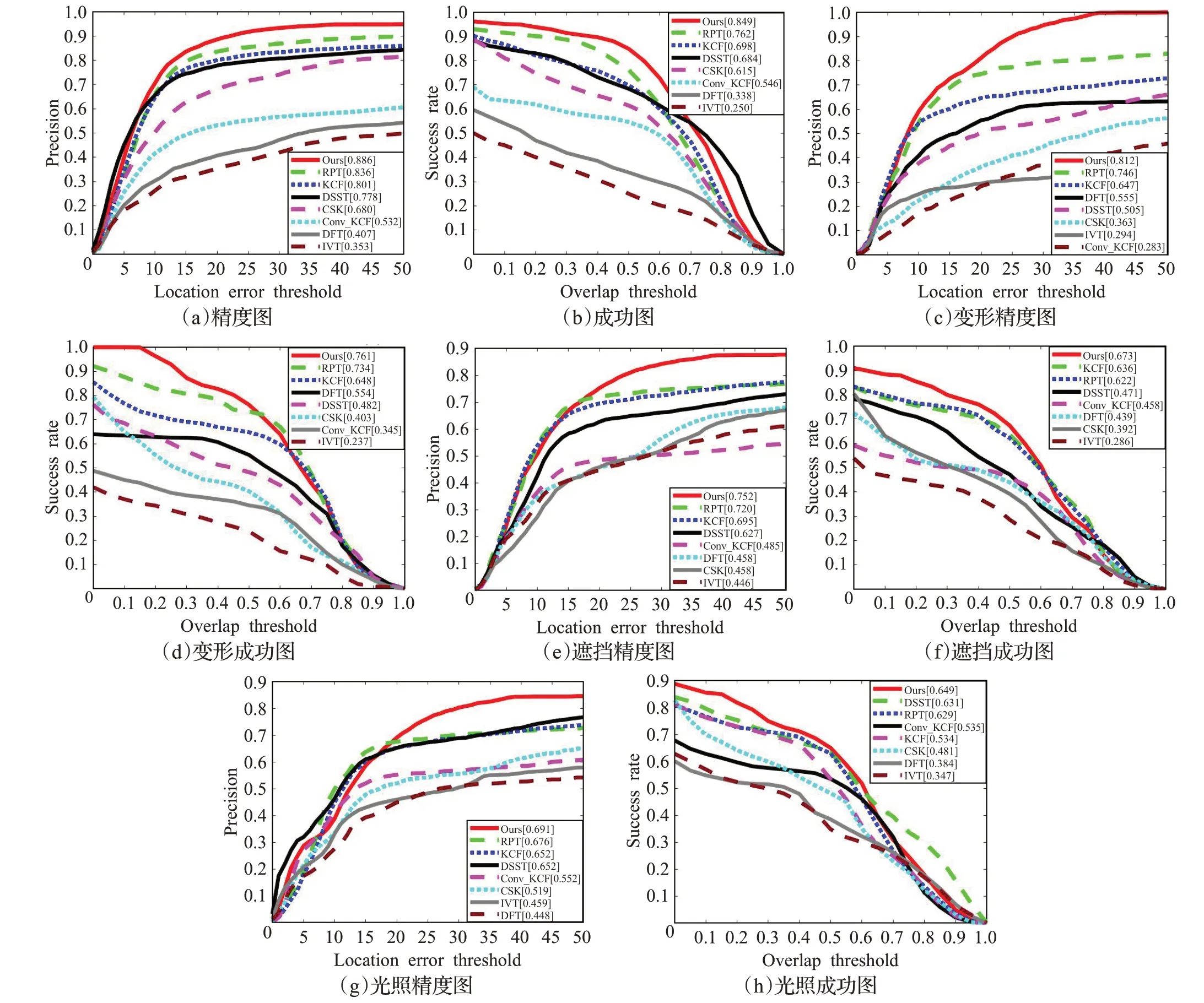
图1 精度和成功图

5 结束语

在本文中，利用有效块跟踪框架，该框架试图识别和利用可靠的块粒子用以实现运动目标跟踪。为了有效地找到可靠的块，使用块粒子的两个正交特性：可跟踪性和运动相似性，以估计可靠块粒子的分布。在找到可靠的块粒子后，预测和更新这些块粒子。通过跟踪有效的块粒子，可以处理多样化的运动目标。本文使用的响应图的基础跟踪方法是KCF，又基于KCF使用的HOG在某些特征提取方面的不足，选择将颜色直方图和梯度直方图特征进行线性融合，提高在获取响应图的精准度。通过与几个先进跟踪方法的实验表明，本文方法可以稳定、准确地进行目标跟踪。但由于本文采用了粒子重采样，工作总量比较多，所以该算法平均速度仅为0.67帧/s，速度较慢，今后需要进一步优化。