区块链51%双花攻击的进化博弈及防控策略研究
王 雷,任 南,李保珍
1.江苏科技大学 经济管理学院,江苏 镇江212003
2.南京审计大学 国家审计大数据研究中心,南京 211815
1 引言
双花问题是指在数字货币系统中,由于数据的可复制性,存在同一笔数字资产因不当操作被重复使用的情况。双花攻击曾经是传统在线支付中困扰多年的难题,Nakamoto提出的区块链技术通过对每一个区块加时间戳保证了交易记录的真实性,一定程度上减小了双花攻击的概率[1]。但在基于POW(Proof Of Work)共识的区块链中,挖矿节点通过工作量证明的方式竞争记账,如果节点占有超过全网50%的算力,就可以创造一条长于公链的侧链,使公链中的交易被回滚,借此完成双重花费,这种双花攻击也叫51%双花攻击[2]。另外,Pinzón(2016)还提出了种族攻击和芬妮攻击两种新的双花攻击,前者是通过给向自己支付的交易中加入更多的交易费用实现双花,后者则是通过控制区块的广播时间实现双花[3]。随着算力的市场流动性越来越强,节点现在可以通过租借、加入矿池等多种方式积攒算力,2018年比特币黄金BTG(Bitcoin Gold)就遭到了51%双花攻击,恶意节点预先准备了大量算力完成套现,最终系统损失超过1 800万美元。因此双花攻击正成为区块链中不可忽视的安全隐患。
针对这个问题,有学者从攻击者的动机和平台的安全防控两个角度对区块链中不同的双花攻击进行了研究。对于51%双花攻击的产生动机,Chaudhary运用时间自动机模型验证工具证明了比特币中的51%双花攻击成功概率是比较高的[4];Liao提出少数攻击者可以通过联结理性节点的方法增加51%双花攻击成功的概率[5];Biais证明在交易价格满足某些条件时尝试51%双花攻击是有利可图的,但要求投入大量的算力[6]。对于51%双花攻击的防控策略,Budish提出交易成本必须和节点攻击可能获取的最大利益呈正相关关系[7]。Westerlund提出通过主节点和矿工的双层共识机制消除51%双花攻击[8]。Liu研究种族攻击和芬妮攻击,他认为这两种攻击的对象都是接受零确认的商家,只要在多次确认的基础上完成交易,便可有效规避风险[9]。
上述研究并未过多关注双花攻击中节点间的相互作用以及策略的动态变化,不过一些学者已经尝试从博弈角度对区块链中的另外一些安全问题进行过分析。Kiayias曾经指出,通过博弈方法研究区块链中的安全问题,可以更深入的理解不同个体间如何竞争与合作[10]。Sapirstein分析矿工联合形成矿池进行的自私采矿攻击,并对区块链底层协议做适当改进[11]。唐长兵主要研究区块链中的区块截留攻击,并提出基于零行列式的优化方法[12]。Liu[13]和Easley[14]则分别把交易费用作为矿工选择矿池和算力竞争问题中的重要因素进行博弈分析。Abadi构建博弈模型证明了POW共识不是激励兼容的[15]。Liu提到可以基于波动理论和混合策略博弈理论,找到防止区块链网络攻击的最佳策略[16]。
区块链中的双花攻击在本质上是一个经济问题,节点间关于是否攻击进行博弈,选择基于自身收益最大化的策略,节点的策略选择相互之间也会产生影响。因此,本文选择针对双花攻击中破坏力较强的51%双花攻击,构建了节点群体的进化博弈模型,以揭示节点策略的动态演化趋势,并通过推导进化博弈策略,预测51%双花攻击出现的概率;同时,把交易价格和交易费用作为进化博弈模型中的两个重要变量,探讨变量在取值改变时对博弈结果产生的影响;最后,基于前面得到的结论,本文从交易费用和交易价格两个方面提出51%双花攻击的防控策略。
2 51%双花攻击的进化博弈分析
2.1 51%双花攻击中的进化博弈问题
传统博弈论采用“完全理性”的假设,要求参与者有完美的判断和预测能力,然而事实上个人决定容易犯错,集体决策也经常失准[17]。针对这个问题,Smith[18]和Price结合达尔文的自然选择理论创立了进化博弈论,认为参与博弈的个体是“有限理性”的。在进化博弈论中,每个参与人都是重复从群体中随机抽取对手并进行博弈,参与人既可以通过自己的经验获得决策信息,也可以通过观察其他参与人的决策并模仿而获得决策信息。他们之间的策略均衡不是通过迅速的最优化计算得到,而是需要经历一个学习调整的过程。进化稳定策略是进化博弈论中的核心概念,是指如果群体中的大多数个体选择进化稳定策略,那么小的突变者群体就不可能侵入到这个群体中,也代表系统此时处于进化稳定均衡。Taylor[19]之后提出了著名的复制动态模型,用来描述单群体策略的动态过程。随着进化博弈理论研究的深入,该理论在经济学、社会学、生态学领域都有非常广泛的应用。
51%双花攻击是区块链中最为典型且破坏力较强的一种双花攻击,在这种攻击中实际上也包含了一个关于进化博弈的策略选择和均衡问题。在区块链系统中,所有节点组成一个节点群体,每个节点关于是否选择51%双花攻击都拥有一个初始策略,之后节点重复从群体中随机选取其他节点进行博弈,在这个过程中采用策略收益较低的节点会改变自己的策略,转向模仿有高收益的策略,而低收益的策略逐渐被淘汰,经过这样不断的学习与调整后节点群体最终会达到一个均衡状态,即群体中的所有节点都选择进化稳定策略。因此,本文构建区块链中51%双花攻击的进化博弈模型,对节点策略的动态进化情况进行分析。
2.2 研究假设与基本参数
首先与实际情况相结合,对于51%双花攻击模型做出如下假设条件:
(1)节点选择攻击时消耗的算力成本足够大,足以使节点顺利完成攻击,并且两个节点选择攻击时的算力成本相同。
(2)当进行博弈的两个节点都选择攻击时,为了减少各自的算力成本消耗,他们会选择在同一条侧链上合作挖矿。
(3)两个节点购买商品的价格,以及挖矿所获得的交易费用奖励和新币奖励都是相同的。
(4)每个区块都只包括一条交易记录。
(5)不考虑由币的市价变化引起的节点收益变化。
另外,本研究模型中的基本参数包括:参与者节点i和节点j;参与双方的策略Si和Sj,可选的策略集均为{攻击,不攻击};初始状态下选择攻击策略的概率为x(0≤x≤1),则选择不攻击策略的概率为1-x,进化稳定策略用x*表示;参与双方的收益函数分别为Ui(Si,Sj),Uj(Si,Sj);参与双方与第三方商家的交易分别为i1、j1,发送给自己的用于双重支付的交易分别为i2、j2,无i和j参与的其他交易用k表示;第三方商家商品的价格为p;对一个区块进行挖矿消耗的算力成本为h;挖矿获得的奖励包括:每笔交易中由交易发起人承担的交易费用f,每个区块产生后由系统发放的新币b。基于博弈双方不同的策略组合,节点的收益会是由p、h、f、b组合而成的函数。
2.3 51%双花攻击进化博弈模型
两个节点基于是否进行51%双花攻击的问题进行博弈,策略组合包括以下四种情况:Si=攻击,Sj=攻击;Si=攻击,Sj=不攻击;Si=不攻击,Sj=攻击;Si=不攻击,Sj=不攻击。
(1)当i和j都选择攻击时,i从第三方商家购买某商品价格为p,另外支付交易费用f广播到网络中,交易会被挖矿节点记录到公链上;接着i重复利用上笔交易(i1)中的币p发送给自己,并投入较高的算力成本h在另一条侧链中挖矿,将这笔交易(i2)记录在侧链中,i作为矿工获得相应的交易费用与新币奖励;之后i继续在这条侧链上挖矿,并获得相应的奖励;j也选择攻击,并且与i选择同一条侧链,攻击流程与i完全相同。由于i和j在算力方面的优势,最终通过合作挖矿使侧链的长度超过公链,两者第一笔交易消费的金额p都回到自己账户,商品也在自己手中,因此i、j分别完成双花攻击。具体流程如图1(a)。
节点i的收益由以下几部分组成:交易i1中获取的商品价格p,支付的交易费用f;交易i2中支付的交易费用f,通过挖矿获取的交易费用奖励f和新币奖励b,消耗的算力成本h;对网络中的其他交易k挖矿获取的奖励f+b,消耗算力成本h。
综上,节点i的收益:Ui(攻击,攻击)=p+2b-2h,节点j的收益与i完全相同:Uj(攻击,攻击)=p+2b-2h。
(2)当i选择攻击,j选择不攻击时,i和j分别从商家购买价格为p的商品,并支付交易费用f后被矿工记录到公链上;接着i重复利用上笔交易(i1)中的币p发送给自己,并通过挖矿将这笔交易(i2)记录在侧链中,作为矿工获得相应的奖励;之后i继续挖矿并将j的交易(j1)和其他交易k记录在侧链中,并获得相应的奖励。最终侧链长度超过公链,i第一笔交易(i1)的金额p回到自己账户,i完成双花攻击。具体流程如图1(b)。
节点i的收益由以下几部分组成:交易i1中获取的商品价值p,支付的交易费用f;交易i2支付的交易费用f,通过挖矿获取的奖励f+b,消耗算力成本h;交易i1中获取的奖励f+b,消耗算力成本h;其他交易k中获取的奖励f+b,消耗算力成本h。节点j的收益包括交易j1中支付的交易费用f。
综上,节点i的收益:Ui(攻击,不攻击)=p+f+3b-3h,节点j的收益:Uj(攻击,不攻击)=-f。
(3)当i选择不攻击,j选择攻击时,情况与(2)正好相反。
节点i的收益:Ui(不攻击,攻击)=-f,节点j的收益:Uj(不攻击,攻击)=p+f+3b-3h。
(4)当i和j都选择不攻击时,i和j各支付p购买商品,并支付交易费用f后被记录到公链上,具体流程如图1(c)。

图1 双花攻击博弈流程图
节点i的收益:Ui(不攻击,不攻击)=-f,节点j的收益:Uj(不攻击,不攻击)=-f。
综上,节点i和j的收益矩阵见表1。

表1 51%双花攻击节点收益矩阵
根据收益矩阵,当节点选择攻击策略时,可以求出其期望收益为:
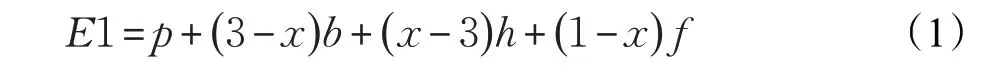
当节点选择不攻击策略时,其期望收益为:

节点选择攻击策略的概率为x,选择不攻击策略的概率为1-x,因此节点的平均期望收益为:

博弈类型动态变化的速度取决于两个因素,即可模仿对象数量的大小(该类型博弈方的比例)和模仿对象的成功程度(该类型博弈方收益超过整体平均收益的幅度)[20]。由式(1)~(3)得到节点选择攻击策略的复制动态方程为:位图如图3。博弈有两个进化稳定策略,即x*1=0和x*2=1,博弈结果取决于x的大小,如果x位于区间

图2 p<h-b时的动态相位图
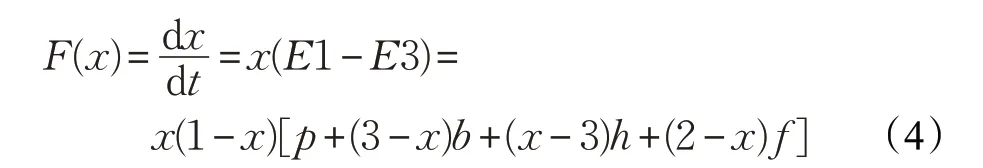
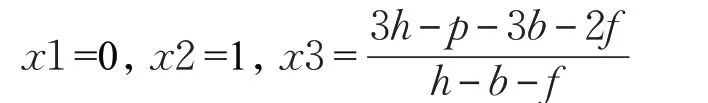
由于在常见的区块链平台(比特币BTC、比特现金BCH)中,新币奖励一般几年才变动一次,因此本模型中假设新币奖励b为定值,另外假设算力成本h也是足够大的定值。将商品价格p和交易费用f作为模型中的两个变量,根据p和f的不同取值,节点的进化稳定策略可分以下几种情况进行讨论:不攻击策略;相反,如果x位于区间1),则收敛到x*2=1,节点选择攻击策略。分界点越大,节点选择攻击策略的可能性越小。当f≥时,复制动态相位图与图2(c)相同,x*=1是节点的进化稳定策略,节点在长期都会选
由于在复制动态相位图上,复制动态曲线与横坐标轴相交并且交点处切线斜率为负的点就是进化稳定策略[21]。所以当p<h-b且f≤时,复制动态相位图如图2(a),该博弈有唯一的进化稳定策略,即x*=0,表明节点在长期都会选择不攻击策略。当p<h-b且<2h-2b-p时,如图2(b),x*=是唯一的进化稳定策略。表明节点选择攻击策略的比例为,比例越小节点选择攻击策略的可能性就越小。当p<h-b且f>2h-2b-p时,如图2(c),x*=1是进化稳定策略,表示即使有少量节点选择不攻击策略,随着不断的学习和调整,最终所有节点都会采取攻击策略。
(2)在h-b<p<2h-2b条件下,分三种情况进行分析,当f<2h-2b-p时,复制动态相位图与图2(a)相同,x*=0是进化稳定策略,节点在长期都会选择不攻击策略。当2h-2b-p<f<时,复制动态相

图3 h-b<p<2h-2b时的动态相位图
(4)在p>3h-3b条件下,无论f的取值是多少,复制动态相位图都和图2(c)相同,x*=1是节点的进化稳定策略,节点在长期都会选择攻击策略。
综上所述,当交易价格和交易费用处于不同区间时,节点的进化稳定策略如表2所示。
3 仿真分析
3.1 仿真环节设计
为了更直观地体现节点进行51%双花攻击意愿的进化过程,本文使用Matlab软件进行仿真分析。首先对p、b、h、f进行赋值,根据进化博弈模型中得到的结论,并结合实际情况,本文将算力成本h和新币奖励b分别设置为定值200元和80元,然后将交易价格p分为四种情况,在每种情况下交易费用f有多种取值,具体赋值情况如表3所示。

表2 节点的进化稳定策略分类情况

表3 关键参数赋值情况 元
2.3节中已经得到了节点选择策略的复制动态方程:F(x)==x(1-x)[p+(3-x)b+(x-3)h+(2-x)f],把经过赋值的p、b、h、f依次填入该方程形成节点策略迭代和进化的函数。
接着在[0,1]区间内以0.05为间隔,取20个不同的节点攻击的初始概率值(0、0.05、0.1、0.15……),再设置所观察节点攻击概率变化的时间区间。根据节点策略迭代和进化的函数,以时间t为横坐标,以节点选择攻击策略的概率x为纵坐标,绘制20种初始条件下节点攻击意愿进化情况的曲线。
然后根据交易价格和交易费用的不同取值对每种情况下节点攻击意愿的进化情况进行具体分析。
3.2 交易价格在最小区间
当交易价格为60时,p小于临界值h-b。首先当交易费用f=200时,节点的攻击意愿进化情况如图4(a),可以看出进化稳定策略是x*=1,所有节点在长期都会选择攻击策略。接着减少交易费用使f<2h-2b-p,当f=170时的节点攻击意愿进化情况如图4(b),进化稳定策略是x*=4/5,表明会有4/5的节点选择攻击策略,1/5的节点选择不攻击策略,此时攻击概率仍然较高。进一步减少交易费用使f=100,节点攻击意愿进化情况如图4(c),此时节点的进化稳定策略变为x*=0,无论节点选择不同策略的初始比例是多少,最终所有节点都会选择不攻击策略。

图4 交易价格在最小区间的攻击意愿进化情况
3.3 交易价格在第二区间
当交易价格为200时,p大于临界值h-b,小于临界值2h-2b。首先当交易费用f=100时,节点攻击意愿进化情况如图5(a),进化稳定策略是x*=1,所有节点都会选择攻击策略。减少交易费用使当f=70时节点的攻击意愿进化情况如图5(b),此时的进化稳定策略取决于x的初始值,x<2/5时所有节点都会选择不攻击策略,相反会选择攻击策略。进一步减少交易费用,f=20时的节点攻击意愿进化情况如图5(c),可以看出节点的进化稳定策略变为x*=0,节点都会选择不攻击策略。
3.4 交易价格在第三区间
当交易价格为280时,p大于临界值2h-2b,小于临界值3h-3b。首先当交易费用f=60时,节点攻击意愿进化情况如图6(a),此时的进化稳定策略是x*=1,节点都会选择攻击策略。减少交易费用使f<,f=20时节点的攻击意愿进化情况如图6(b),此时进化稳定策略取决于x的初始值,x<2/5时所有节点都会选择不攻击策略,相反会选择攻击策略。
3.5 交易价格在最大区间
当交易价格为400时,p大于临界值3h-3b,首先当交易费用f=100时节点攻击意愿进化情况如图7(a),此时的进化稳定策略是x*=1。减少交易费用至f=50,节点攻击意愿进化情况如图7(b),进化稳定策略还是x*=1。因此无论交易费用f为多少,节点最终都会选择攻击策略。

图5 交易价格在第二区间的攻击意愿进化情况

图6 交易价格在第三区间的攻击意愿进化情况
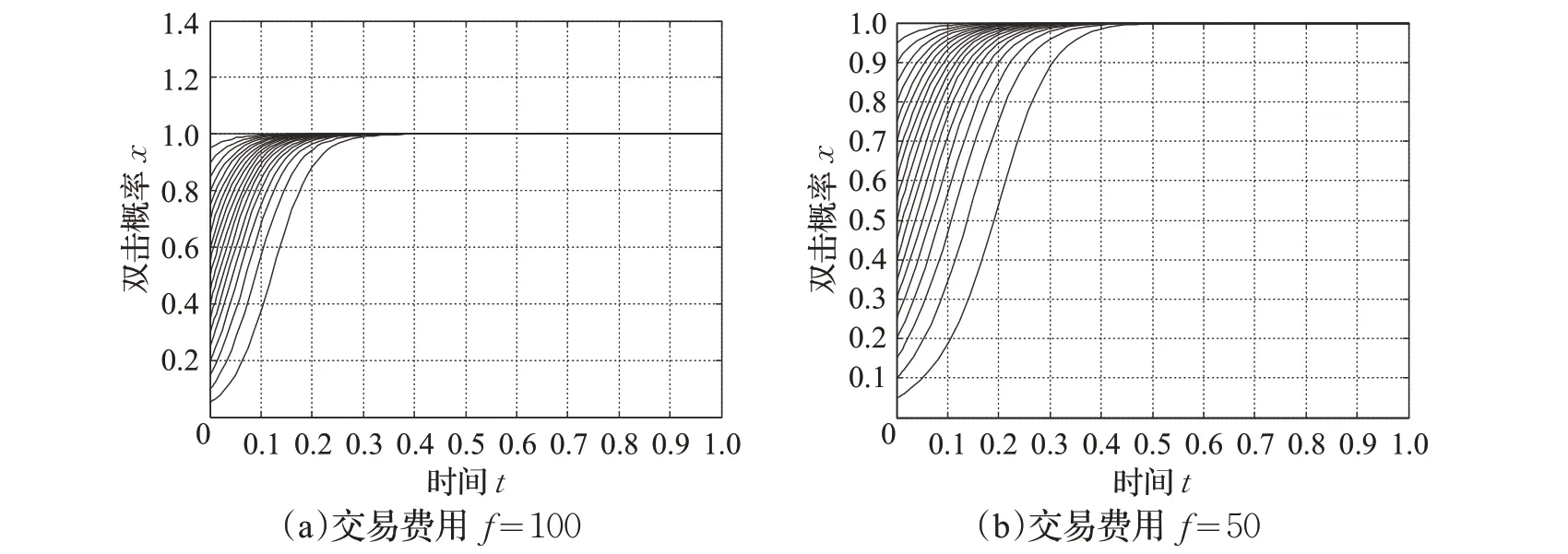
图7 交易价格在最大区间的攻击意愿进化情况
经过上述仿真实验可以看出,当交易价格和交易费用取不同值时,实验结果与进化博弈模型中的结论完全吻合。
4 对策与建议
通过对区块链中的51%双花攻击进行进化博弈分析,本文揭示了51%双花攻击的内在机理,基于相关内在机理,尝试提出如下风险防控策略:
(1)平台调控与市场调节相结合
对于比特币、以太坊这些知名的区块链平台,交易费用都是由矿工和交易发起者自愿决定的,属于市场调节机制,然而这种方法会造成交易费用的极不稳定,为节点进行51%双花攻击提供了机会。为了有效抑制51%双花攻击的出现,平台需要制定严格的交易费用标准。对于不同交易价格的交易,都要设定相应的交易费用最大值,交易发起者需在规定的范围内支付交易费用,这样会使节点基于收益最大化的考虑趋向于选择不攻击策略。此外,考虑到对矿工的激励,可由矿工来决定每笔交易的最低费用。这种将平台调控与市场调节相结合的方法,有利于在提高区块链安全性的基础上保证资源配置的效率。
(2)根据价格区间划分相应风险监控等级
虽然规范交易费用可以有效抑制51%双花攻击的出现,但无法完全消除,因此需要制定平台的监督机制,制约和惩罚节点的恶意行为。根据前文得到的结论,不同交易价格区间节点攻击意愿的进化情况不同,受到抑制的效果也不同。因此可以基于不同价格将平台中的交易划分4个风险等级,由低到高分别为:稍有危险、一般危险、高度危险、极其危险。风险等级更高的交易进行攻击的可能性更大,产生的危害也更大,需要对其进行重点监督。在监督过程中收集和分析与风险相关的各种信息,预测可能发生的风险,及时提出预警。对于已发生的攻击行为,立即限制节点的交易和挖矿活动,并进行处罚。这种方法可以更有效及时地减小51%双花攻击产生的危害。

