可表示一致模的加法生成子

侯晓东，李 钢

（齐鲁工业大学（山东省科学院）数学与统计学院，济南 250353）

三角模（t-norm）和三角余模（t-conorm）作为重要的合取型和析取型聚合算子[1]，被广泛应用于模糊控制、模糊聚类、信息聚合和人工智能等领域.Fodor 等[2]提出了一致模（uninorm）的概念，使得三角模和三角余模得以推广和统一，为相关模糊理论的研究奠定了基础[3-4].一致模广泛应用于神经网络、专家系统、图像处理和信息融合等领域.文献[5]综述了各类一致模的相关结论，并指出其应用领域.本文研究可表示一致模的加法生成子，得到当满足一定条件时，加法生成子可由给定的一致模构造出来，同时得到了基础三角模和基础三角余模的加法生成子，最后给出了所得结论在可表示一致模的序关系以及对应剩余蕴涵方面的应用.本文结论可应用于信息决策、优化控制和模糊逻辑等领域.

1 预备知识

首先给出相关概念.

定义 1[2]对于二元算子 U：[0，1]× [0，1]，若Ax、y、z∈[0，1]，有

（1）U（x，y）=U（y，x）；

（2）U（x，U（y，z））=U（U（x，y），z）；

（3）U（x，y）≤U（x，z），y≤z；

（4）Ee∈[0，1]，使得 U（e，x）=x，Ax∈[0，1].

则称U 为一致模，其中e 称为U 的单位元.当e = 1时，U 退化为三角模T；当e =0 时，U 退化为三角余模S.

由一致模U，定义三角模TU和三角余模SU为

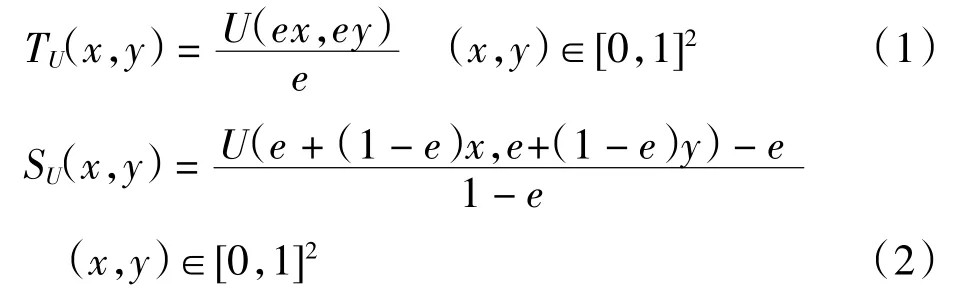
TU和SU分别称为U 的基础三角模和基础三角余模[2].

定义2[5]给定一致模U，单位元e∈]0，1[，若存在函数 h（x）：[0，1]→，h（x）是连续的且严格递增的，h（0）=-∞，h（e）=0，h（1）=+∞，使得

U（x，y）=h-1（h（x）+h（y））

其中：（x，y）∈[0，1]2{（0，1），（1，0）}，则称U 为可表示一致模，称h（x）为U 的加法生成子.

可表示一致模U 的加法生成子不唯一，若h（x）是 U 的加法生成子，则 kh（x）（k >0）也是 U 的加法生成子.记AU为U 的所有加法生成子构成的集合.

定理1[6]设一致模U 的单位元e∈]0，1[，则U 是几乎连续的（即U 在（x，y）∈[0，1]2{（0，1），（1，0）}连续）当且仅当U 是可表示一致模.

可表示一致模通常由给定的加法生成子构造.本文讨论逆问题，即，给定可表示一致模U，研究如何构造U 的加法生成子.

2 主要结论

下面的定理2 给出了如何利用可表示一致模U构造其加法生成子h（x）.

定理2设U 为可表示一致模，单位元e∈]0，1[.若加法生成子h（x）在]0，1]存在连续导数，且满足

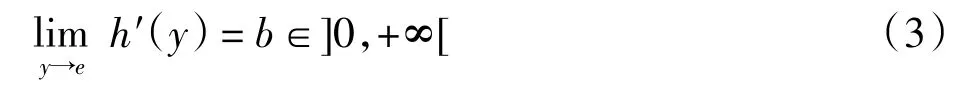
则 h（x）可表示为：

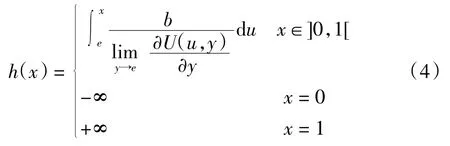
证明（1）由于 h（x）在]0，1]存在连续导数，则h（x）的连续性显然.

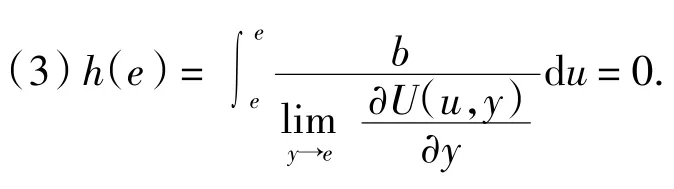
（4）由反函数的导数公式[7]可得

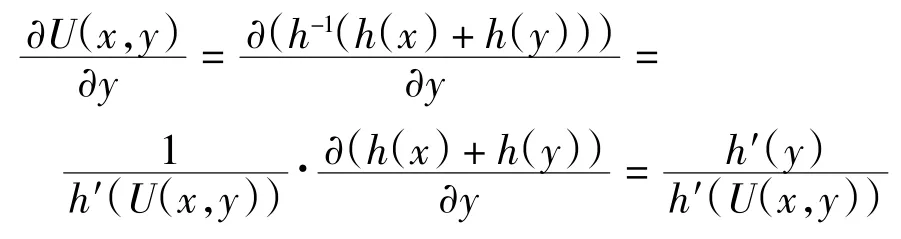
所以有

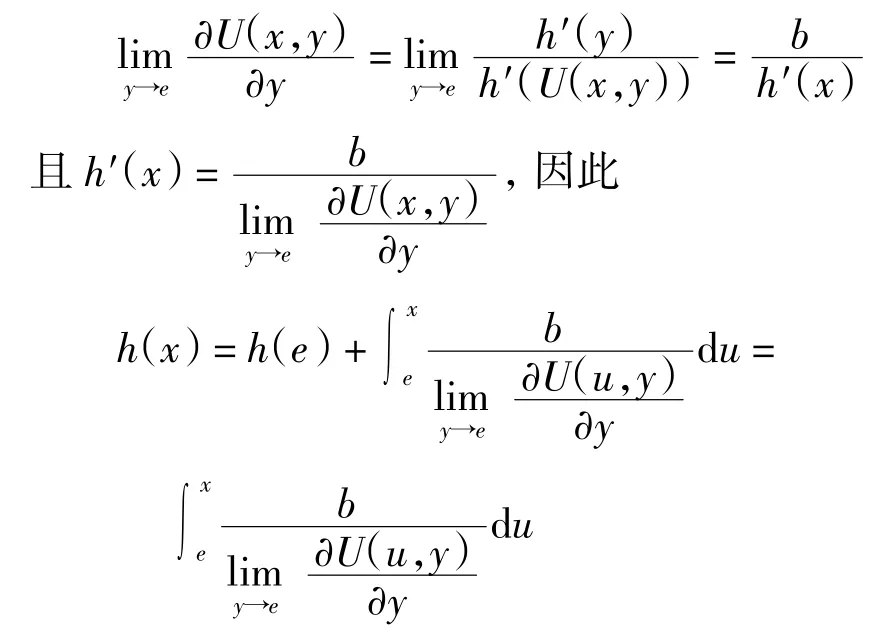
综上定理得证.

下面给出可表示一致模U 的基础三角模和基础三角余模的加法生成子.

推论1设U 为可表示一致模，单位元e∈]0，1[，则有

（1）U 的基础三角模TU的加法生成子为

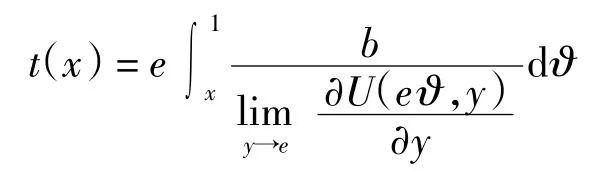
（2）U 的基础三角余模SU的加法生成子为

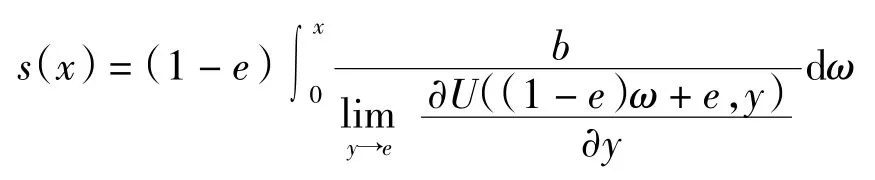
证明（1）当 x≤e 时则有

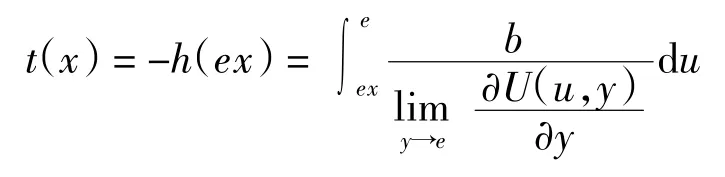
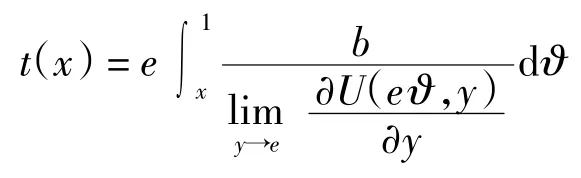
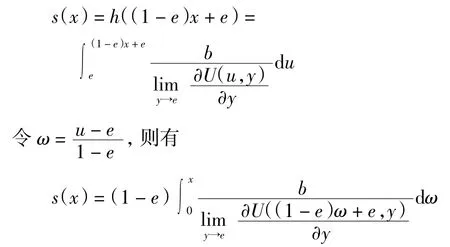
命题设U 为可表示一致模，单位元e∈]0，1[.若存在一致模U 的一个加法生成子h（x）∈AU满足则AU中任意加法生成子k（x）均满足

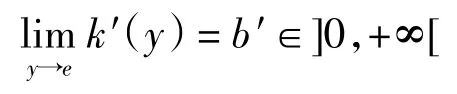
证明设加法生成子h（x）∈AU，则对于任意加法生成子 k（x）∈AU，存在 q >0，使得 k（x）=h（x）·q[2]，因为则有

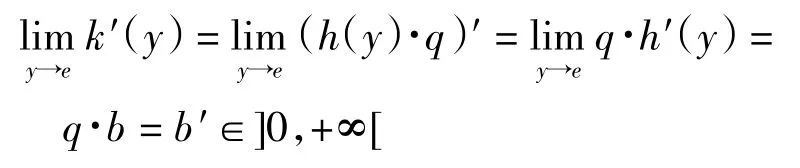
由定理2 和命题可得到如下推论2.

推论2设U 为可表示一致模，单位元e∈]0，1[，其加法生成子在]0，1]存在连续导数.若存在加法生成子也是一致模U 的加法生成子，其表达式为

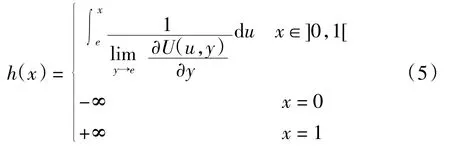
例1设一致模U 的表达式为

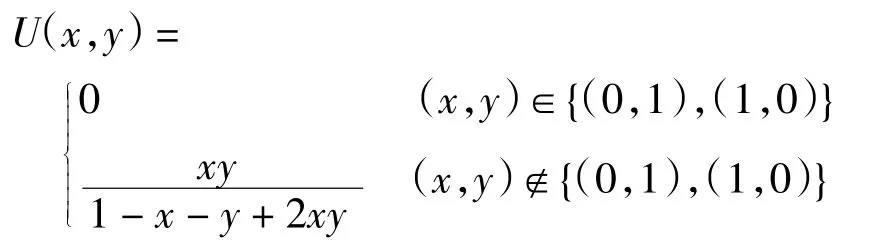
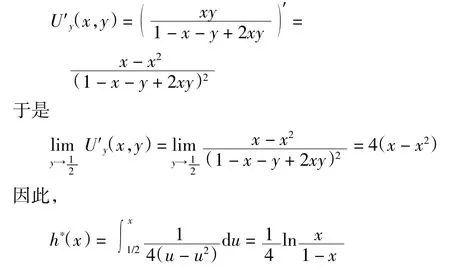
当k > 0 时，kh*（x）仍是U 的加法生成子，4h*（x）=即为文献[2]中的算例.

注：若定理2 中的式（3）不成立，则无法用式（4）或式（5）构造加法生成子.

例 2若一致模 U 可由加法生成子h（x）构造，h（x）具有表达式

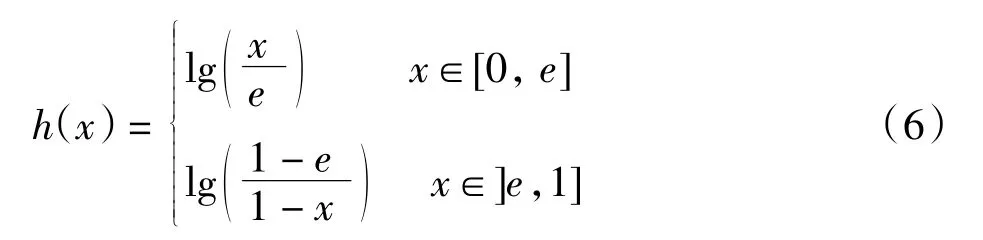
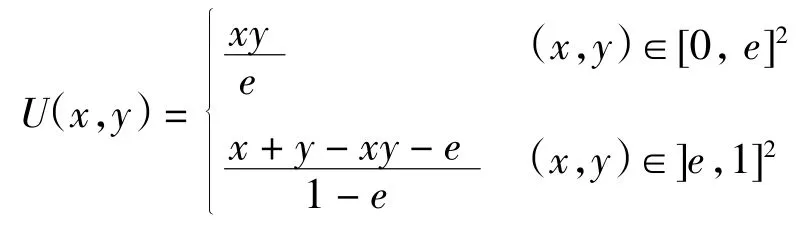
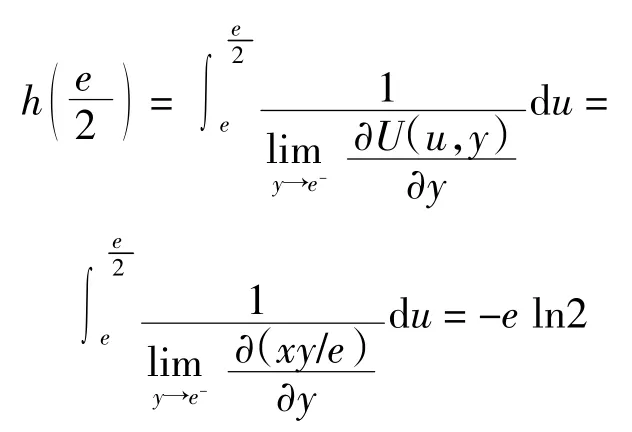
3 应用

下面给出定理2 在讨论可表示一致模的序关系以及对应剩余蕴涵方面的应用.

定理3[8]设U1和U2为单位元相同的可表示一致模，则 U1≤U2→h1h2-1是超可加的，其中 h1、h2分别为 U1、U2的加法生成子.

例3给定一致模

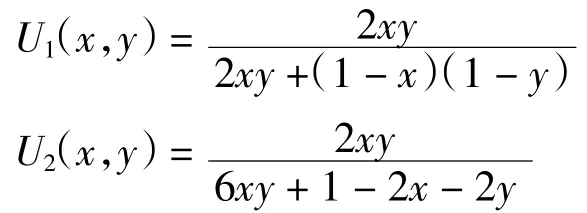
由定理1 可知U1和U2均为可表示一致模.由推论2可计算得到U1和U2的加法生成子分别为

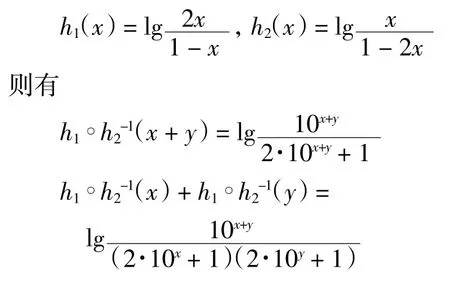
由文献[9]的定理7 知可表示一致模诱导的剩余蕴涵可通过加法生成子表示为

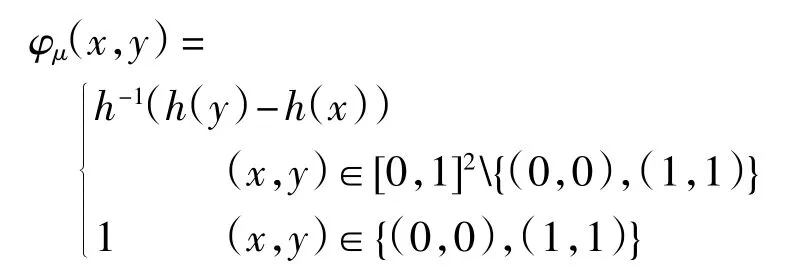
利用推论2 可以直接写出例3 中的U1诱导的剩余蕴涵，当（x，y）∈[0，1]2{（0，0），（1，1）}时，

当（x，y）∈{（0，0），（1，1）}时，φμ（x，y）=1.