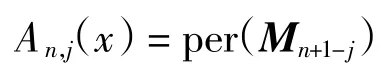限制欧拉多项式的一些组合性质

张旭彤，张 彪

（天津师范大学数学科学学院，天津 300387）

欧拉多项式是组合数学中一类极其重要的多项式，欧拉数也是一类非常重要的组合数，它们在组合数学中有着非常重要的应用和意义，因而被广泛研究并取得了丰硕的成果[1-2].1998 年，Ehrenborg 等[3]通过对欧拉数加以限制给出了一个关于单位立方体中相邻2 个切片混合体积的组合解释.在此基础上，2008年，Brenti 等[4]在经典欧拉多项式和欧拉数的基础上，通过限制排列的第一位提出了限制欧拉多项式和限制欧拉数的概念，并研究了它们的相关性质.限制欧拉多项式又被称为j-欧拉多项式[2]，它在几何方面有很多应用.文献[4]应用限制欧拉多项式研究了布尔复形在重心重分下的f 向量和h 向量的相关理论.文献[5]通过构造回文的限制欧拉多项式证明了布尔复形在重心重分下的γ向量是一个均衡单纯复形的f 向量.文献[6]通过对s-欧拉多项式加以限制研究了推广欧拉多项式的实零点问题.文献[7]通过证明半开的格平行立方体是j-欧拉多项式的线性组合而证明了格分割多面体的h*多项式是实零点的.

本研究提出了一种新的限制欧拉多项式的概念，它是通过同时限制排列第一位和最后一位而得到的，并给出了这种新的限制欧拉多项式的一个简单性质的组合证明.利用该性质，给出了2 个关于原限制欧拉多项式与新的限制欧拉多项式关系的性质，并给出了对应的组合证明.此外，本研究还利用文献[8-9]提出的一个组合双射证明了在限制排列最后一位的n元排列集合中超越数和下降数的同分布性.

在给出主要结论之前，首先给出相关概念.

定义 1设 n、i 是正整数，且 1≤i≤n，定义 n 元排列的表示为

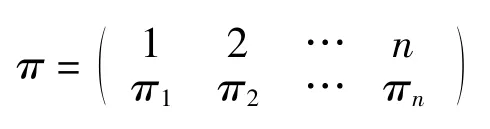
其中 πi∈[n]={1，2，…，n}.

由于第一行是固定的，因此可以去掉第一行得到排列的一行表示为π=π1π2…πn.用π-1（i）表示数字i在排列π中所对应的位置，并用Sn表示n 元排列组成的集合.

定义 2设n、i 是正整数，且1≤i πi+1，则称第 i 个位置为排列 π的一个下降位，用 Des（π）={i∈[n-1]：πi> πi+1}表示排列π的下降集，用des（π）表示下降集的元素个数，称为排列π的下降数.

定义 3设 n、k 是正整数，且 0≤k≤n - 1.用A（n，k）表示欧拉数，定义欧拉数为集合

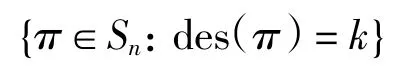
的元素个数；用An（x）表示欧拉多项式，其定义为

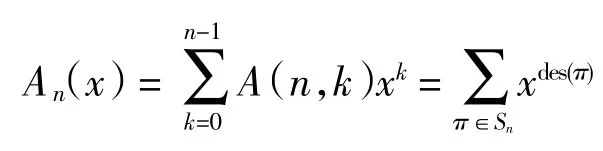
定义 4[4]设n、j 是正整数，且1≤j≤n，用An，j（x）表示j-欧拉多项式，用an，j（k）表示j-欧拉数.定义j-欧拉数为集合

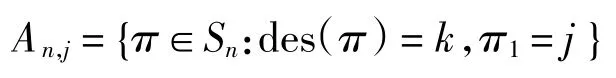
的元素个数；利用j-欧拉数可以定义j-欧拉多项式为

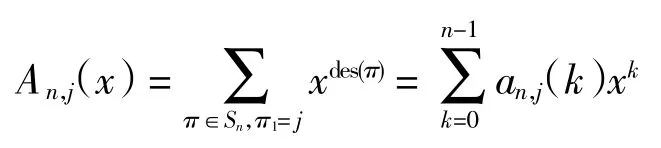
对于给定的排列 σ= σ1σ2…σn∈An，j，令 πi=n+1-σn+1-i，构造排列 π = π1π2…πn∈Sn，排列 σ 的第一位 j使得排列π的第n 位为n+1-j，即可得到如下性质.

性质 1[4]设 n、j 是正整数，且 1≤j≤n，则 j-欧拉多项式满足

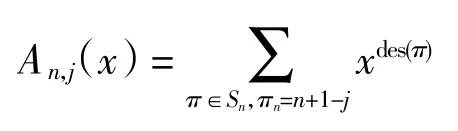
此外，j-欧拉多项式也可以看作是经典欧拉多项式的细化，它们有如下关系：

性质 2[4]设 n、j 是正整数，且 1≤j≤n，则 j-欧拉多项式满足

1 （i，j）-欧拉多项式

受到j-欧拉多项式的启发，本文进一步定义了同时限制排列的第一位和最后一位的情况.

定义 5设 n、i、j 是正整数，且 1≤i≠j≤n，0≤k≤n-1，用An，i，j（x）表示（i，j）-欧拉多项式，用an，i，j（k）表示（i，j）-欧拉数.定义（i，j）-欧拉数为集合

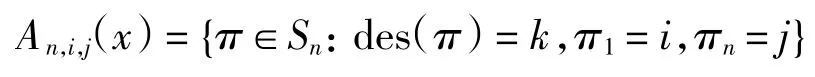
的元素个数；利用（i，j）-欧拉数可以定义（i，j）-欧拉多项式为

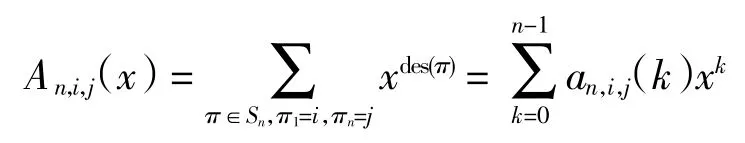
由（i，j）-欧拉多项式的定义，可以得到以下引理.

引理设 n、i、j、r 是正整数，并且 i+r≤n，j+r≤n，则有

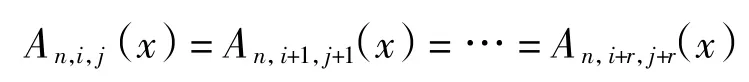
证明首先证明An，i，j（x）= An，i+1，j+1（x），其中i、j≤n+1.构造 An，i，j到 An，i+1，j+1的映射，对于给定的排列 p∈An，i，j，将排列 p 中所有小于 n 的数字加 1，再将 n 变为 1，则得到排列 p′∈An，i+1，j+1，p 映射为 p′.如给定排列 p =34251∈A5，3，1，经该映射后得到排列 p′=45312∈A5，4，2，并且有 des（p）=des（p′）=2.由于逆映射可通过该映射唯一确定，故容易验证该映射是一个双射.虽然这个双射破坏了原先排列p 中n 与其后面元素所形成的下降位，但是同时也在排列p′中1 的位置前面形成了新的下降位，而且其他连续数对之间的关系没有改变.因此，这个双射没有影响下降数的大小，也就自然得到了

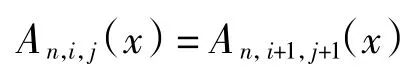
按照以上方法，同理可以证明

以下 2 个定理给出了 j-欧拉多项式与（i，j）-欧拉多项式之间的关系.

定理1设n、j 是正整数，且1≤j≤n，则有

证明 由j-欧拉多项式An，j（x）的定义可得An，j（x）=An+1，j，n+1（x），再由引理可得

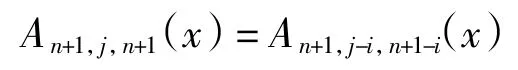
定理 2设 n、i、j 是正整数，且 1≤j≤n，1≤i≤n-j，则有

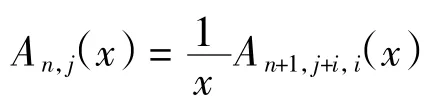
证明对于给定的排列 σ= σ1σ2…σn∈An，j，构造映射 φ：An，j→An+1，j+1，1，使得排列 π = π1π2…πn+1=φ（σ）∈An+1，j+1，1.具体构造为：将排列 σ 中的每个数字加1，再将数字1 放到排列的最后一位，则得到排列π∈An+1，j+1，1，其中：π1=j +1，πn+1=1.如对于排列 σ=23154∈A5，2，其中：n=5，j=2，des（σ）=2，则通过映射可得 π = φ（σ）=342651∈A6，3，1，其中：π1=3，π6=1，des（π）=3.由于φ的逆映射可通过φ唯一确定，故容易验证该映射是一个双射.该双射增加了一个πn与πn+1=1 形成的下降位，但是并没有影响其他数对之间的大小关系，故有 des（π）=des（σ）+1.因此可得

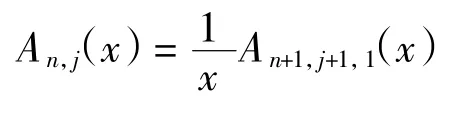
由引理可得

因此定理得证.

2 超越数和下降数在集合An，j中的同分布性

本节证明在集合An，j中超越数和下降数的同分布性.

定义 6[10]设排列π∈Sn，用exc（π）表示超越数，其定义为

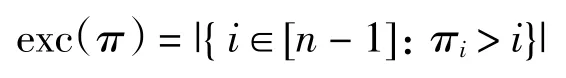
其中满足条件的i 称为排列π的一个超越位.

定理3设n、j 是正整数，且n≥1，则对于固定的 j∈[n]，有

证明首先构造组合双射如下：对于给定的排列σ=σ1σ2…σn∈Sn，构造 φ：Sn→Sn，使得 π = π1π2…πn=φ（σ）.定义 σ0=0，并且令 k∈[n].若对于 m> k，有σk > σm，则令 πσk+1=σk；否则，在排列σ中找到第1个在σk左边并小于σk的元素，若该元素为σi，则令πσi+1=σk.由于该双射表明了在集合Sn中下降数和超越数的同分布性，因此利用该双射可得

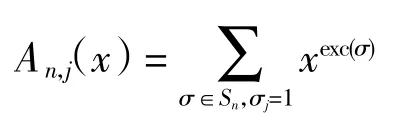
这是由于在排列σ∈An，j中没有比1 更小的元素，并且σ0=0 是第一个小于1 的元素，因此第一个元素j在经过双射φ变换后使得排列的第j 个位置变成了1，令 σ=σ1σ2…σn∈φ（τ），则有 σj=1.

对于给定的排列 σ=σ1σ2…σn∈Sn，令 πi=n+1-σ-1（n+1-i），构造排列φ（σ）=π=π1π2…πn∈Sn，则i 是排列π中的一个超越位当且仅当σ-1（n+1-i）是排列σ中的一个超越位.这是因为，若i 是排列π中的一个超越位，则πi>i，则有n+1-σ-1（n+1-i）>i，变形得σ-1（n+1-i）i，即πi>i，所以i 是排列π中的一个超越位.因此，映射φ是一个双射.此外，经过双射φ变换后，排列σ中的第j 位σj=1 确定了排列π中最后一位为πn=n+1-j.因此可得

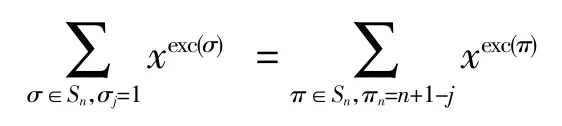
下面给出一个与定理3 的证明有关的例子.

例对于排列 τ =23541∈A5，2，其中：n=5，j=2，des（τ）= 2，通过定理 3 的双射 φ 可得 σ =φ（τ）=41253∈S5，其中：σ2=1，exc（σ）=2.再经过定理 3 的双射 φ 变换后，得 π= 25134∈S5，其中：π5= 4，exc（π）=2.

定义7设n ×n 阶矩阵M=（mi，j），用per（M）表示矩阵M 的积和式，定义为

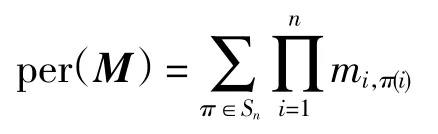
由定理3 得到的在限制排列最后一位的前提下下降数和超越数的同分布性，以及矩阵积和式的定义，可得如下推论.

推论设矩阵M 为

将矩阵M 划掉第n 行和第j 列得到的子矩阵记为Mj，则有