低能见度环境下多出口场馆人群疏散研究

鲍东宾，马飒飒，张 磊，魏欢欢

1.河北工业大学 人工智能与数据科学学院，天津300130

2.总装军械技术研究所，石家庄050003

1 引言

虽然火的出现和使用极大地促进了人类文明的发展，但它所造成的火灾成为人类自诞生以来最大的敌人之一[1]。根据我国消防管理局的统计数据，2013年至2016年间，平均每年都有36万起火灾事故发生，平均死亡人数为1 852，平均受伤人数为1 357，直接财产损失44亿元，其中引起火灾的主要原因是电气原因[2]。通常火灾都会导致照明系统瘫痪等能见度较低的情况，了解低能见度环境下的疏散机制可以有效地减少火灾造成的人员伤亡，是当下一个十分重要的研究课题。

为了研究疏散人员动态行为，科研人员已经提出了许多具有里程碑意义的疏散仿真模型，包括离散模型和连续模型。元胞自动机模型[3]和格子气模型等属于常见的离散模型，而Helbing提出的社会力模型是比较著名的连续模型，被广泛研究。该模型将影响人员疏散的心理因素、社会因素和外在环境因素用力的形式表示，通过加速度方程计算疏散行人的运动速度[4]。相比于其他模型，社会力模型可以很好地模拟出疏散个体的行为特征和一些常见的疏散现象，比如“出口处呈拱形”“快即是慢”等现象，此外也可以呈现出一些疏散人群自组织现象，比如聚集行为、羊群行为等[5-6]。

文献[7]采用社会力模型，定义了指数形式的团体吸引力，研究了人员疏散过程中有领导者存在的小团体对疏散结果的影响。文献[8]通过使用元胞自动机模型建立了行人跟随领导者的疏散模型，研究团组行为对疏散进程的影响。文献[9-11]研究了低能见度条件下包括安全疏散路标和数字图像在内的疏散指导设施对疏散进程的影响。文献[12]在烟雾弥漫的隧道进行了疏散实验，研究了有限能见度条件下疏散个体选择出口的行为。文献[13]通过改进社会力模型，研究了烟雾弥漫的环境下不同行人数量的疏散时间和视野半径的关系。文献[14-15]研究了有限能见度环境下单出口房间的疏散动态和疏散领导者对疏散时间的影响。

以上文献对低能见度环境下人群疏散行为分析不全面且只研究了单出口房间的疏散情况。针对以上出现的不足，本文基于社会力模型，建立了低能见度环境下多出口场馆人群疏散仿真模型，研究了低能见度环境下多出口场馆人群疏散行为，以及能见度范围变化及疏散领导者对疏散时间和出口利用率的影响。

2 低能见度环境下疏散行为分析

低能见度环境下，待疏散个体的能见度范围有限，从环境获得的信息相对较少。因此，在这种环境下对大型公共场馆结构的熟悉程度直接影响到个体在紧急疏散中采用的行为决策，如是否能独立决策疏散方向，是否受周围其他个体影响等。

根据待疏散人员对疏散场馆结构熟悉程度的差异，将场馆内所有人员分为普通人和疏散领导者两类。

（1）疏散领导者

一般大型室内公共场所都会在场馆中心区域随机位置或指定位置设置一定数量的疏散领导者领导人群疏散。疏散领导者熟悉场馆结构，即使在能见度较低的环境下也能准确地判断疏散出口位置。疏散开始后，领导者选择向距离自己最近的出口进行疏散。另外，疏散领导者一般保持较低的疏散速度以便更好地领导周围个体疏散。

（2）普通人

普通个体对场馆结构不熟悉，只能依靠能见度范围内的环境信息决定疏散方向。若个体能够看见出口，则其会直接朝出口方向疏散。若个体看不见出口但在疏散领导者影响范围内，则会一边向疏散领导者靠近，一边保持与疏散领导者一致的疏散方向。若个体既看不见出口也不在疏散领导者影响范围内，则会跟随能见度范围内大多数个体的疏散方向进行疏散。

3 模型建立

3.1 社会力模型

社会力模型是根据牛顿第二定律建立疏散个体受到的作用力和其运动两者之间的关系。文献[4]将疏散个体的运动用3个力的合力表达：期望力f0i；人与人之间的相互作用力fij；人与墙之间的作用力fiw。数学表达式如式（1）所示：

式（1）中，mi表示个体i的质量，vi(t)是个体i当前时刻的速度。

（1）期望力

期望力f0i表示个体期望在时间τi内由目前的实际速度vi(t)达到期望速度)的意愿，数学表达式如下：

式（2）中，v0i(t)为期望速度大小，单位向量e0i(t)为期望速度方向。

（2）个体之间的相互作用力

个体之间的相互作用力fij包括两者之间的心理作用力fsij及两者接触时的物理作用力fpij，数学表达式如式（3）所示：

心理作用力fsij反映了个体i希望与个体j保持一定距离的意愿，表达式如下：

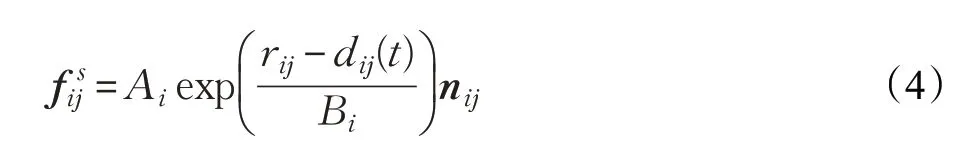
式（4）中，Ai表示个体之间心理作用力的强度，Bi表示个体之间心理作用力的作用范围，rij=ri+rj表示个体i和个体j的半径和，dij(t)表示t时刻个体i和个体j质心之间的距离，nij表示个体j指向个体i的单位向量。

式（5）中，tij(t)表示个体j与个体i的切线方向单位向量。

（3）个体与墙壁或障碍物之间的作用力

人与墙之间的作用力fiw类似与个体之间的相互作用力，数学表达式如下：

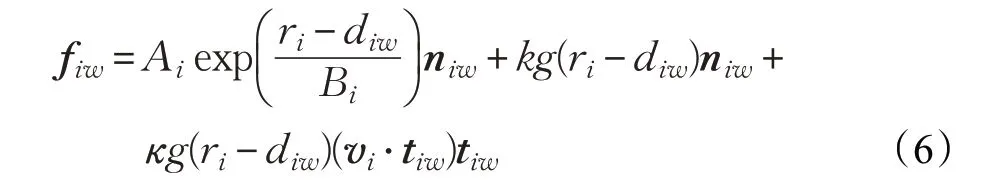
其中，diw表示个体到墙或障碍物表面的距离，)表示墙或障碍物指向个体的单位向量，

3.2 疏散领导者吸引力

借鉴文献[7]描述的团体吸引力，在低能见度环境下，普通个体因为不熟悉场馆结构，不能够获取出口位置信息，所以对疏散领导者的依赖心理更强，期望靠近领导者并和领导者一起疏散。

本文定义了一个指数形式的作用力，表示疏散领导者i对其影响范围内的普通个体g的吸引力，它与个体之间的心理排斥力类似，但方向相反，数学表达式如下：

式（7）中，Ei表示吸引力的强度，Fi表示吸引力的作用范围，rig是普通个体g和疏散领导者i的半径之和，dig是普通个体g和疏散领导者i之间的距离，nig表示疏散领导者i指向个体g的单位向量。

3.3 期望速度方向选择

在疏散过程中，每个疏散个体都有一个期望速度方向，指向期望目标位置。因为个体对疏散场馆的熟悉程度不同，所以制定以下规则来描述个体选择期望方向的过程。

（1）疏散领导者和出口附近个体

疏散领导者熟悉场馆结构，出口附近个体能够看见出口，他们都会选择距离自己最近的出口为期望目标位置，文献[4]对期望速度方向的表达式如下所示：

式（8）中，Pi表示t时刻距离领导者i的最近出口位置，ri表示t时刻个体i的实际位置。

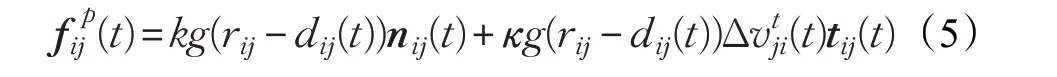
此外，疏散领导者为了更好地指导疏散，其期望速度一般比正常行人要小，认为v0j=αv0i，0＜α≤1，本文取α=0.5。

（2）受领导者影响的普通个体

当疏散个体是普通个体且在领导者影响范围内时，个体会倾向于向领导者的位置方向移动，同时按照领导者的指导保持与领导者一致的期望速度方向。期望速度方向由式（9）表示：

式（9）中，e0j表示领导者j的期望速度方向，ρ是一个距离决定参数，由式（10）决定。

其中，dij表示个体i和领导者j之间的距离，δ表示个体i的能见度范围。

（3）不受领导者影响且看不见出口的普通个体

当普通个体不在领导者影响范围内且不能看见出口时，个体会跟随能见度范围内大多数个体的疏散方向进行疏散。类似于文献[13]对个体从众行为的描述，期望速度方向由式（11）给出：

式（11）中，e0j表示个体j的期望速度方向，dij表示个体i和个体j之间的距离。

4 仿真及结果分析

使用Visual Studio软件搭建低能见度环境下多出口场馆人群疏散仿真模型。仿真参数设置如下：对于每个个体，半径r=0.6 m，质量m=80kg，正常行人的期望速度v0i=1 m/s,常量k=1.2×104,κ=2.4×105,Ai=2 000,Bi=0.08 m,Ei=200 N,Fi=0.48 m,能见度范围δ=5 m。疏散人群数量为200人，场馆大小为15 m×15 m，出口数量为2，每个出口宽度为1 m。由于仿真具有随机性，本文中每次仿真都是随机生成疏散人员位置，统计的疏散数据均为同一情形仿真20次得到的平均疏散结果，以减少数据偶然误差。

（1）无疏散领导者

模拟场馆内所有待疏散个体都是普通人时的疏散情形，如图1所示。其中黑色圆点代表普通待疏散个体。

从图1中可以看出，疏散开始后，出口附近的个体自发地向出口方向聚集，看不见出口的个体则向能见度范围内人多的方向聚集，最终在两个出口附近都呈现了拱形或类半圆形现象；疏散过程中，由于能见度范围较低，大多数个体不能合理地选择疏散方向，导致两出口拥堵人群数量相差很大，出口利用率较低。

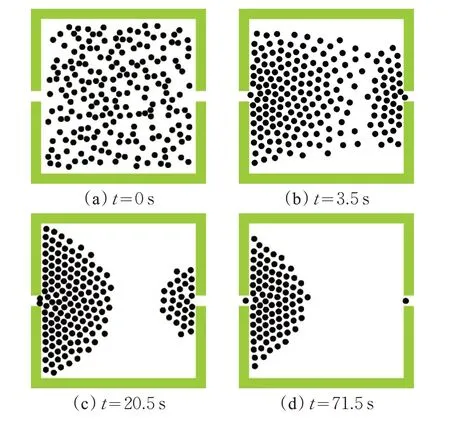
图1 不同时间的疏散情形（无领导者）

不同能见度范围下，无领导者疏散数据统计结果如图2所示。

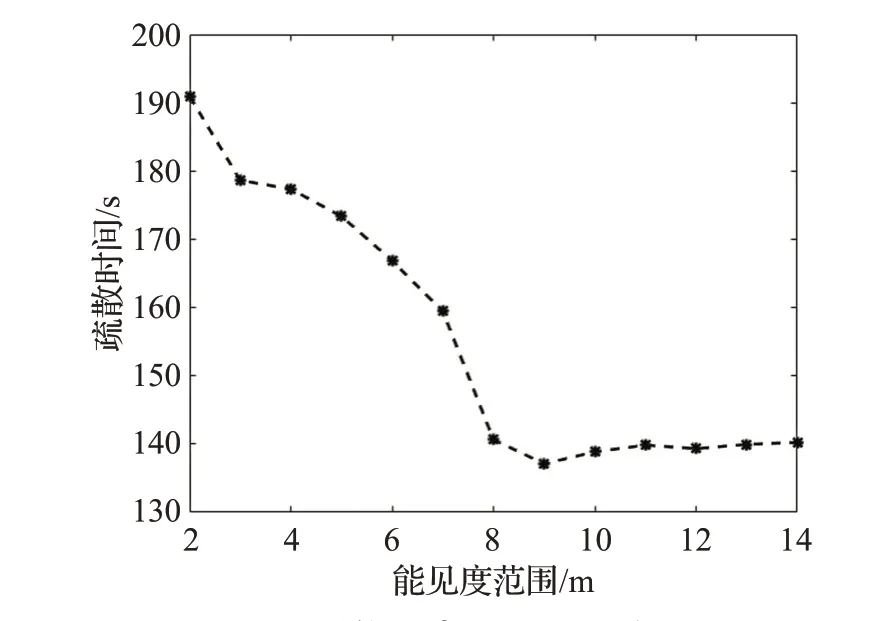
图2 不同能见度范围的疏散时间

从图2中可以看出，能见度较低时，疏散时间较长，疏散效率较低，随着能见度范围的增加，疏散时间明显减小。当能见度范围增加到一定程度后，疏散时间不再受能见度范围变化的影响。

（2）随机初始位置领导者

以两个随机位置疏散领导者为例进行仿真，如图3所示。其中红色圆点代表疏散领导者，黑色圆点代表普通待疏散个体。

从图3中可以看出，疏散开始后，出口附近的个体自发地向出口方向聚集，疏散领导者由于熟悉场馆结构，能够独立判断，选择距离自己最近的出口方向进行疏散；疏散领导者附近看不见出口的个体则向最近的疏散领导者靠近，同时保持与疏散领导者一致的疏散方向；由于疏散领导者的影响，待疏散人数较多时，拱形或类半圆现象并不明显，随着待疏散人数的减少，才逐渐恢复拱形或类半圆现象。

不同数量随机位置领导者疏散数据统计结果如图4所示。

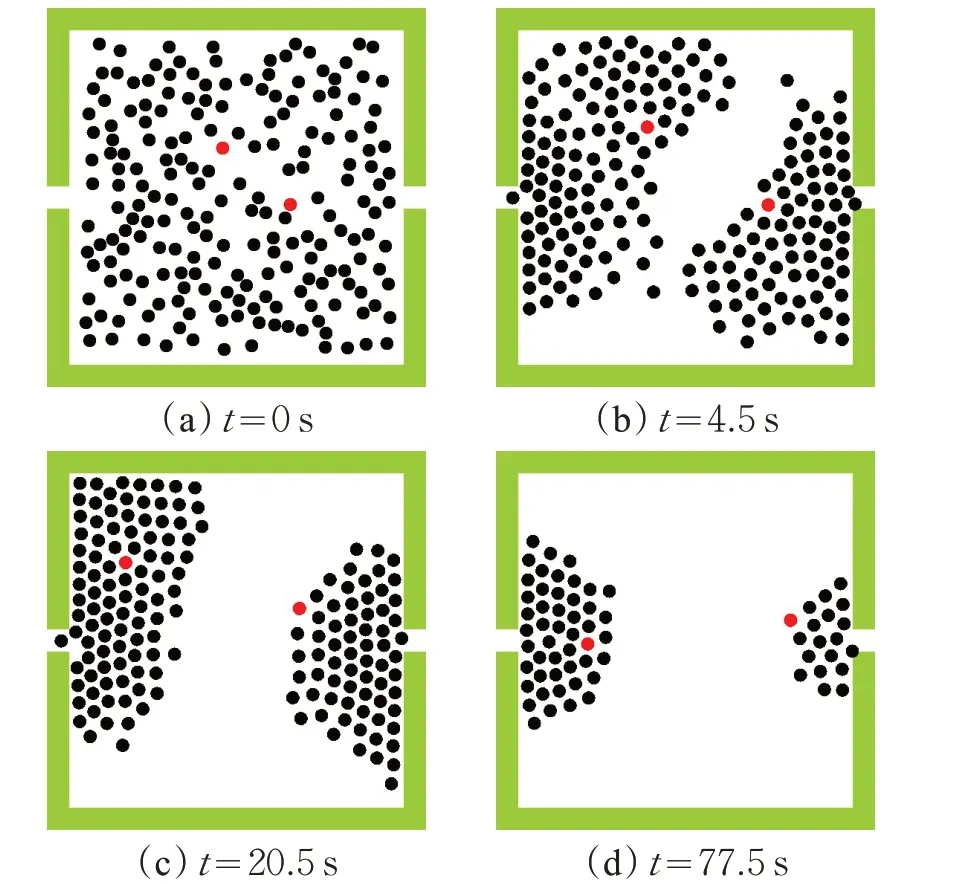
图3 不同时间的疏散情形（随机位置领导者）

图4 不同数量领导者的疏散时间

从图4中可以看出，对于双出口疏散场所，仅设置一个领导者时，疏散时间要比无领导者时疏散时间长。只有设置两个以上领导者时，疏散时间才会低于无领导者时的疏散时间，且随着领导者数量的增加，疏散时间在逐渐缩短。

（3）指定初始位置领导者

针对文中仿真场景，将领导者设置在两出口正前方1/4场馆宽度处可以使领导者的影响范围最大，如图5所示。其中红色圆点代表指定初始位置的疏散领导者，黑色圆点代表普通待疏散个体。

从图5中可以看出，基本疏散情形与图3类似；由于优化了疏散领导者的初始位置，两个出口附近拱形或类半圆形现象比较明显，两出口聚集的待疏散个体数量相对平均，出口利用率较高。

低能见度环境下多出口场馆无领导者、随机初始位置领导者和指定初始位置领导者三种情形各仿真20次得到的平均疏散数据对比如图6所示。

从图6中可以看出，在仿真的初始阶段，三种疏散情形疏散人数随疏散时间变化曲线的斜率基本相同。随着时间的推移，无领导者和随机位置领导者疏散情形曲线的斜率大幅度变小，即单位时间内成功疏散的人数变少，疏散效率降低。并且随机位置领导者曲线斜率减小幅度低于无领导者曲线斜率减小幅度，说明疏散领导者的存在和位置优化能够提高低能见度环境下多出口场馆人群疏散效率。

图5 不同时间的疏散情形（指定位置领导者）

图6 三种疏散情形对比

5 结论

为了研究低能见度环境下多出口场馆人群疏散行为和疏散领导者对疏散结果的影响，本文在基本社会力模型的基础上加入了领导者吸引力和能见度范围的限制，建立了各类待疏散个体期望速度方向的表达式。仿真结果表明，本文提出的低能见度环境下多出口场馆人群疏散仿真模型是可行的，在低能见度环境下多出口场馆中可以通过设置不少于出口数量的领导者和优化领导者初始位置两种方式来提高疏散效率。本文对研究低能见度环境下人员疏散规律及制定疏散方案具有参考价值。