基于人工探路蚁的波浪滑翔机路径规划

陈 茜，高军伟，官 晟

1.青岛大学 自动化学院，山东 青岛266071

2.国家海洋局 第一海洋研究所，山东 青岛266061

1 引言

波浪滑翔机是一种新型的自主海洋环境监测平台，它的出现对海洋环境监测领域有着划时代的意义。由于波浪滑翔机的航行动力来源于海洋波浪，海洋中无穷尽的波浪可以保证波浪滑翔机持续航行，波浪滑翔机的水面浮体上安装有太阳能板和储能电池，海洋中白天充足的光照可以保障波浪滑翔机上的各种仪器用电，具有超长航时、绿色无污染、自主运动等特点[1-2]。

由于波浪滑翔机的自身结构原理，海洋环境因素的变化对波浪滑翔机的航行速度和航行路径有很大的影响，海洋环境复杂，暗流、暗礁、海风巨浪等不确定因素导致波浪滑翔机的路径规划一直是一个研究的难点。针对复杂的海洋环境和波浪滑翔机的结构特点，有必要设计有效的路径规划算法。常规的移动机器人路径规划工作环境较为简单，动力速度可控，不适用于波浪滑翔机。在常规寻路算法的基础上应考虑到波浪滑翔机的航行速度不可控，尽可能利用海洋环境。本文以栅格法划分海洋区域，一方面方便整合海洋环境因素，将海洋环境通过速度预测模型归一化为动态航行速度并引入到状态转移规则中。另一方面，海洋广阔平坦，单位面积区域内海洋环境极为相似，栅格法的精度问题对算法性能影响较小。海洋环境复杂，常规蚁群算法极易陷入死锁，引入人工探路蚁对可行节点情况提前探索，与文献[3]中在转移规则中引入上一节点数组来增加逃逸能力和文献[4]中引入交叉算子来增加逃逸能力相比耗时更短。改进后的算法不仅优化了自身结构，提高了收敛速度，避免了局部最优解，更充分利用了海洋环境因素，使得波浪滑翔机能在复杂的海洋环境中快速、安全地航行到目标点。

2 算法描述

2.1 环境建模和波浪滑翔机的数学模型

波浪滑翔机的结构如图1所示，分为水面浮体和水下翼板两大部分，中间由一条4 m左右的柔性脐带缆连接，在波浪的起伏推动下航行[5-6]。

图1 波浪滑翔机结构图

路径规划中首先要考虑的问题是环境建模，常用的环境建模方法有栅格法、可视图法等。本文采用栅格法对波浪滑翔机的连续航行环境进行离散化处理，以二维数据的形式运算更方便高效，每个栅格可以用序号和直角系坐标表示，它们之间的换算关系如下：

在栅格环境中，波浪滑翔机可以认为是二维平面空间中的粒子，有8种运动方向，如图2所示。由于实际中，波浪滑翔机的外观尺寸较大，障碍物的面积应该按照波浪滑翔机的半径大小膨化，确保波浪滑翔机沿障碍物边缘航行时不会撞到障碍物，并且障碍物面积不满一个栅格时应按照一个栅格计算[7]，充分保障航线的安全性。

图2 10×10栅格建模示意图

海洋环境中除了暗礁障碍物外，波浪、风速、洋流等因素也应该考虑进栅格环境内。

Smith等提出了线性回归模型来预测波浪滑翔机的速度[8]。波浪滑翔机在海面航行的时候，其自身配置是恒定的。通过测量有效浪高、波峰周期、浅层流、表层流、风速和方向等海洋环境因素，线性权衡6个海洋环境因素，推导了一个波浪滑翔机速度的预测模型[9]。波浪滑翔机速度预测模型如下：

其中，ysog是波浪滑翔机的对地速度；xwht是有效波高；xwpp是波峰周期；xwdir是波浪滑翔机航向与波向的差值；xwnd是风速在航向轴向的分量；xadcp是表层流速在航向轴向的分量；xhfr是浅层流速在航向轴向的分量[9]。因实际中采集到的海洋环境数据有限，仅考虑影响速度的主要因素，将速度预测模型简化如下：

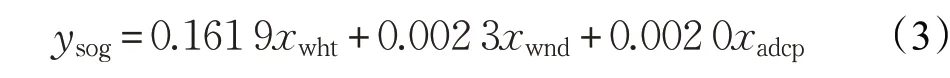
将所有海洋环境因素归一化为预测速度来改进栅格法，除去黑色障碍物栅格，对白色自由栅格进行不同程度的蓝色填充来表示归一化的波浪滑翔机预测速度，从而使其应用于波浪滑翔机进行海洋环境建模。海洋环境栅格建模如图3所示。

2.2 常规蚁群算法简介和相关改进

蚁群算法是1994年Dorigo提出的一种相对成熟的群体智能优化算法，通过模拟自然界蚂蚁觅食的行为来寻求最优解。根据外界环境的变化，蚁群算法可以动态做出反应，且鲁棒性能好，被广泛应用于旅行商问题（Traveling Salesman Problem，TSP）、车辆调度问题、网络路由问题等实际问题中[10]。

图3 海洋环境速度预测栅格建模

常规蚁群算法的节点选择方式是根据节点之间的信息素浓度和启发信息进行概率选择的，在t时刻，蚂蚁k从节点Xi转移到节点Xj的转移概率公式如下：

其中，τij(t)为t时刻节点i到节点j的信息素浓度，α表示信息素浓度的相对重要程度；ηij(t)为t时刻节点i到节点j的实际距离的倒数，β表示启发性因子的相对重要程度[11]。

常规蚁群算法存在收敛速度较慢，搜索范围小且容易陷入局部最优解等缺点。为弥补常规蚁群算法的缺陷，一方面，研究者通过修改蚁群算法自身参数结构来避免局部最优解，例如修改节点转移规则或信息素更新策略；另一方面，研究者通过蚁群算法和其他智能算法相融合来提高收敛速度，避免局部最优解，例如遗传蚁群算法、人工免疫蚁群算法、人工势场蚁群算法等[12-13]。

3 改进蚁群算法

3.1 改进启发函数

海洋环境十分复杂，暗礁丛生，针对复杂航行环境，改进算法引入了障碍物复杂度mark的概念，即在一定区域范围内，障碍物栅格的分布情况。在蚂蚁进行路径搜索时，搜索蚁从起始点S出发，以节点间的信息素和启发信息搜索前进，在进行下一节点选择时，派出探路蚁，为搜索蚁可能前进的方向探索障碍物分布情况，并对此方向的障碍物分布情况进行标准评分。当此方向的评分较高时，说明该方向海况良好，障碍物分布较少；当此方向评分较低时，说明障碍物分布复杂，海况情况复杂，在此方向继续搜索前进的话，可能需要耗费更多时间，或使算法陷入死锁[14]。探路蚁可以让算法规避易死锁的节点，既节约了死锁后逃逸需要的时间，又保证了算法收敛时的稳定性，提高了算法收敛速度。

当搜索蚁进行下一节点选择时，假定搜索蚁Mk的当前位置为Lk，设Lp1为搜索蚁Mk的一个可行栅格，则在Lp1栅格放置一只探路蚁。

第一种情况：当栅格Lp1不在边界处时，则探路蚁沿向量LkLp1的方向移动一个栅格，到达栅格Lr1，探路蚁在以Lr1栅格为中心的（3×3）方形区域进行障碍物复杂情况探索，计算该区域的障碍物复杂度。如图4所示，红色圆形为搜索蚁Mk的位置，它的下一可行节点有Lp1栅格、Lp2栅格等，则对应的红色三角形所在栅格即为对应可行节点探路蚁的位置，对红色虚线范围内的（3×3）栅格进行障碍物分布探索。

图4 障碍物探索位置示意图

第二种情况：Lp1栅格位于边界处，如图5所示，红色圆点为搜索蚁Mk的位置，Lp1是它的下一可行点，但Lp1位于边界位置，不存在沿LkLp1方向的下一节点，则探路蚁的位置为红色三角形所在的栅格，探路蚁以红色三角形栅格为中心进行障碍物分布情况探索。

图5 边界情况下障碍物探索位置示意图

第三种情况：若探路蚁最终的位置栅格在边界的4个角落栅格（栅格序号为1、20、380、400），则该可行节点的障碍物复杂度置0。

综上，每个可行节点gi的障碍物复杂度mark(gi)已求出，将距离启发信息和障碍物复杂度线性权衡，最终得出该可行节点的综合评分S(gi)如下：

其中，Dis(gi)是当前节点gi到目标节点的距离，mark(gi)为节点gi对应的障碍物栅格的个数。因此，新的启发式函数如下：

复杂障碍物的存在，尤其是U型等陷阱类障碍物分布，不仅对算法的性能造成了影响，更对航线的安全性做出了考验，人工探路蚁的提前规避作用，在一定程度上提高了航线的安全性。

3.2 改进信息素更新策略

常规蚁群算法只在迭代时才更新路径上的信息素，这种更新方式不仅影响了算法的收敛速度，还较容易出现局部最优解。为避免上述的缺点，采用局部信息素更新和最优最差奖惩机制迭代信息素更新来改进蚁群算法的信息素更新策略[15]。

（1）局部信息素更新

每一代的每一只蚂蚁在经过某个节点后都对该节点的信息素进行更新，更新方式如下：

其中，ρ为信息素挥发因数，在[0，1]范围内可调；τ0为信息素初始浓度；τij为节点i到节点j路径上的信息素。蚂蚁k经过某节点后，随时间增加，路径上的信息素挥发了一部分，保证了信息素不会残留太多而湮没启发信息，增加了蚂蚁搜索未经过节点的概率，从而避免了局部最优解[16-17]。

（2）最优最差奖惩机制全局信息素更新

t代k只蚂蚁都完成了路径搜索，更新路径的信息素浓度，选择t代所有蚂蚁经过路径中最长的一条路径Lworst和最短的一条路径Lbest，对该路径上的信息素浓度进行更新[18]。

如式（7）、（8）、（9）所示，Δτkij(t)为t代蚂蚁k在路径(i,j)上遗留的信息素。

3.3 动态航行速度

由于波浪滑翔机的航行动力全部来源于海洋环境，其中主要是海洋波浪的起伏带动了波浪滑翔机的航行，因此，与普通机器人路径规划只考虑路径长度不同，波浪滑翔机还要考虑航行时间。海洋环境随所处区域位置和时间变化而变化，是一个动态参量。在环境建模之中，已经将环境因素通过速度预测模型归一化为速度，为方便运算，本文以相邻栅格之间为划分单位，即栅格i到相邻栅格j的速度为Vij(t)。在蚂蚁进行下一节点转移时，应考虑到当前时间当前节点与下一节点之间的速度，若路径长度相同，应先考虑速度快的节点。

综上，引入人工探路蚁来改进启发函数，障碍物复杂度和距离启发信息共同作用形成新的启发函数Hj(t)；整合海洋环境因素，利用预测速度模型求出波浪滑翔机在当前时间地点下的航行速度Vij(t)；利用局部信息素更新和最优最差奖惩机制迭代信息素更新改进蚁群算法的信息素更新策略，得出新的路径上的信息素浓度τij(t)。新的节点状态转移规则如下：

3.4 改进蚁群算法的流程

步骤1初始化海洋环境参数，包括波浪的有效波高、地下水流等环境因素；初始化蚁群算法的参数，包括蚂蚁个数m、迭代次数k、初始时刻路径上的信息素浓度、信息素强度Q、信息素挥发系数等参数。

步骤2栅格建模，利用栅格法将海洋环境离散处理，并根据海洋环境数据，利用预测速度模型，将海洋环境归一化为动态速度。

步骤3所有蚂蚁开始路径选择，依据节点状态转移规则选择下一节点，并将当前节点加入到禁忌表tabuk中。

步骤4判断蚂蚁是否到达终点，若某只蚂蚁到达终点，则局部信息素更新；某代所有蚂蚁完成从起点到终点的搜索后，选出最优局部路径和最差局部路径，全局更新路径上的信息素浓度。

步骤5判断是否达到最大迭代次数，若没有继续迭代循环，达到最大迭代次数后，输出时间和路径长度最优的路线。

4 仿真验证

采用Matlab2014a编程平台进行实验仿真，仿真环境为20 km×20 km的海洋区域，障碍物分布已知。算法中的参数初始化为蚂蚁个数M=50，最大迭代次数K=80，其他参数根据实际仿真效果动态调整[19]。

仿真实验结果如下：

由于改进蚁群算法引入了人工探路蚁，提前对无效或容易使路径陷入死锁的节点进行屏蔽，有效提高了算法的收敛速度。图6为改进算法和常规算法的收敛曲线对比，图7为改进算法和常规算法的仿真路线对比，可以看出，改进算法在第15代左右就收敛并趋于稳定，较常规蚁群算法的25代左右趋于稳定有明显的提升。

图6 改进算法和常规算法的收敛曲线对比

图7 改进算法和常规算法仿真路线对比

图8 常规算法和改进算法仿真路线对比（增加障碍物）

（1）更换仿真环境，增加障碍物分布的复杂情况。在新的静态环境中进行仿真实验，如图8所示，在图7仿真环境的基础上增加了障碍物的复杂情况。常规蚁群算法在遇到障碍物阻挡前进方向时，绕障碍物移动，没有提前探索到障碍物，这增加了路径的长度[20]。而改进蚁群算法提前探索到了障碍物的分布，提前舍弃该节点躲避了障碍物，相较于常规蚁群，路径长度较短，安全性更高。

（2）由于单次算法运行结果有偶然性，为验证改进后算法的有效性，选取两种新的仿真环境，多次运行取平均值。另外，由于节点之间的航行速度不同，且在路径节点选择时已经将速度考虑进去，航行时间和航行路径长度应该都是衡量算法优劣的性能指标。如表1所示，在改进算法和常规算法规划出来的路径长度相近时，改进算法的航行时间更短。改进蚁群算法的总体性能较常规蚁群算法有了明显的提升。

5 结论

本文针对波浪滑翔机的路径规划问题，提出一种改进的蚁群算法。

表1 改进蚁群算法和常规蚁群算法的性能对比

（1）考虑到海洋环境障碍物分布复杂，引入了人工探路蚁，对可行节点方向的障碍物分布情况提前探索，充分避免了算法易陷入死锁的问题，减少了收敛振荡，提高了收敛速度，也提高了航线的安全性。

（2）针对波浪滑翔机的动力特点，将海洋环境因素依据波浪滑翔机环境预测模型归一化为预测速度，并将此因素加入蚁群算法的状态转移规则中，在考虑航线长度的同时兼顾航行速度。

（3）针对蚁群算法信息素更新策略的缺点，增加了局部信息素更新方式，利用最优最差奖惩机制改进了迭代信息素更新策略，增加了蚂蚁的寻优能力，增大蚂蚁搜索范围，避免了局部最优解。

经仿真验证，改进后的蚁群算法完全胜任波浪滑翔机的路径规划任务，即使在复杂的海洋环境中，也可以快速地规划出一条距离短、安全性高的航线。