奇异摄动内层问题的宽度估计及其数值求解

邵文婷，郑烁宇

1.上海第二工业大学 文理学部，上海201209

2.同济大学 数学科学学院，上海200092

1 引言

在物理和工程技术等应用领域，许多从实际问题抽象得到的数理方程中，最高阶导数项前通常含有反映介质性质的摄动参数ε。例如，对流扩散[1-2]和反应扩散方程[3-4]、半导体设备建模的漂移扩散方程、具有大Peclet数的热传导方程等。问题的解作为ε的函数具有奇性层现象：当ε趋于0时，在很小的区域内（区域宽度与ε有关），函数值变化非常剧烈，然而在远离奇性的区域，变化相对比较平缓。这类问题称为奇异摄动问题。

对于奇异摄动问题一般难以得到解析解，而这类跨尺度摄动现象在应用上普遍存在，又使得其迫切需要高效快速的近似解法。目前，随着计算机技术高度发展，数值解法引起了广大科学工作者的重视[5-8]，逐渐活跃为主流方法之一。然而，解具有的奇性层效应给有限差分、有限元等经典的数值方法带来了挑战，往往得不到理想的计算精度。因此，众多学者致力于寻找一种有效的奇性层校正方法，它在实现高精度数值计算上发挥着重大作用。在校正问题的研究中大多涉及了奇性层宽度的探究。文献[9]提出了一种sinh变换，使得离散节点在奇性区域内部进行加密。sinh变换表达式中含有两个分别用来刻画奇性位置和宽度的参数。位置参数可以由渐近理论对解进行先验分析来预判。对于宽度参数，文献[9]和文献[10]分别提出了基于Chebyshev-Páde逼近和Fourier-Páde逼近的估计方法。然而，这些方法在各种实际应用问题中的计算效果一般，可操作性不强。文献[5-6，11]考虑了一类奇异摄动两点边值问题，构造了宽度公式d=σε。在此基础上，文献[12]考虑了一类二维规则区域上指数型边界层问题，提出一种具有“边界消减技术”的区域分裂方法。思路是基于宽度公式对求解区域进行合理的划分，在每个子区域上采用Chebyshev-Tau高精度方法分别进行离散求解。然而，对于公式中系数σ的选取，这些工作均依赖于人为经验，并没有给出一个具体的计算策略。近年来，刘利斌等[4，13-15]在宽度的估计上进行了深入研究。文献[4]针对Shinkin网格在求解反应扩散方程的应用上，构造了以误差范数最小为目标函数的无约束优化问题，采用粒子群优化算法给出了网格过渡点参数的估计。文献[13]将这类宽度估计方法推广至含有两个摄动参数的问题，借助差分进化算法使得边界层区域的计算精度得到大幅度提高。文献[14-15]将利用非线性优化问题来估计宽度参数的想法应用于带有sinh变换的有理谱配点法，加强了sinh变换在求解边界层问题[14]和内层问题[15]中的可靠性。从这些工作中，不难发现寻求一种切实合理的宽度估计方法可以使得奇异摄动问题的数值求解更加精确、高效。

受上述研究启发，本文针对奇异摄动内层问题提出了一种内层宽度的估计方法，并且采用有理谱配点法（Rational Spectral Collocation Method，RSCM）进行高精度数值求解。首先，将计算区域分解为内层区域和区域外部，原问题相应地分解为内层问题和退化问题两部分，其中退化问题不再具有奇性。对于内层问题，引入一个适当的拉伸变换来减弱奇性。为了确定内层宽度，基于区域连接端点处的一阶导数连续性条件设计了一个非线性优化问题。在数值计算上，采用重心形式有理谱配点法进行离散。

重心形式有理谱配点法最早是由Berrut[16-17]等人提出的，其构造特点是将函数在各个节点处的导数值由计算区域上所有离散节点处的函数值加权之和来近似，将微分方程转化为代数方程组进行求解。它的主要优点是如果依据问题的需要引入坐标变换，原方程并不需要随之改变，易于数值离散的操作实现[17]。在计算精度方面，问题的解是充分光滑的，可以达到指数阶收敛速度，因而备受计算数学研究者的关注[5-6，14-15，18-19]。

本文的主要贡献是基于RSCM构造了一种内层宽度估计的数值方法。该方法结合了区域分解和拉伸变换，设计了关于一阶导数连续性条件的优化问题来确定内层宽度，克服了依赖人为经验设定参数的不合理性，或是采用试错法和枚举法造成的计算量和计算时间的大量浪费。此外，本文还考虑了一类非线性奇异摄动两点边值问题的数值计算，采用Adomian分解法[20-21]对原问题进行线性化处理，从而可以将已有的研究工作推广至非线性问题的求解上。数值实验表明，对线性和非线性问题的内层宽度，本文提出的数值方法均给出了一个合理有效的估计，同时在数值解的计算上也得到了令人满意的精度。

2 有理谱配点法

其中，lj(x)为插值基函数：

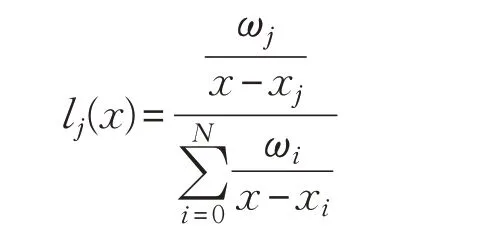
相比经典的拉格朗日型插值函数，重心形式有理插值函数的显著优点是：当离散节点个数较多或需要求解的线性方程组规模较大时，计算引入的舍入误差要小得多，数值稳定性更强。

另一方面，通过简单推导可以直接得到未知函数导数的逼近。设Iu(x)在节点xj处的r阶导数为：

其中一阶和二阶微分矩阵的元素表达式为[9]：

本文取Chebyshev-Gauss-Lobatto点为离散节点，即xj=cos(jπ/N)，对应的权系数为ωj=(-1)jδj,δ0=δN=0.5,δj=1,j=2,…,N-1。

3 区域分解及内层宽度的数值估计

3.1 区域分解

本文考虑如下一类奇异摄动两点边值问题：

其中，0＜ε≪1为摄动参数，ua和ub为已知边界条件。f(x,u)和g(x,u)关于x、u一阶可微。依据f(x,u)和g(x,u)的取值，问题（6）的解在区间端点出现边界层或者区间内部出现内层[14-15]。本文仅考虑内层问题的情况。

假设问题的解在点x∗∈(a,b)的一个小邻域出现内层，宽度d与参数ε有关。不妨假设d=2σεm，其中m＞0,σ＞0为待定参数，这里称σ为宽度系数。

首先，借鉴量纲分析的方法确定m。对问题（6）引入拉伸变换x=εmξ，控制方程转化为：

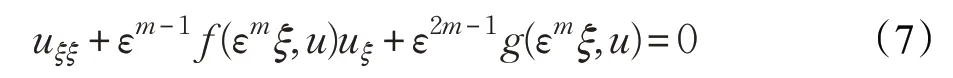
为了使得变换后的方程对于新尺度ξ的量纲是一致的，选取m=m∗使得下式成立：

随后，将求解区域分解为两部分：内层区域[x∗-σεm∗,x∗+σεm∗]和外部区域[a,x∗-σεm∗]，[x∗+σεm∗,b]。对应原问题（6）的解作如下分解。

问题1在外部区域，满足退化问题：

以及

退化问题不含有摄动参数ε，是无奇性问题。一旦确定宽度系数σ，便可以采用第2章介绍的RSCM进行离散求解。

问题2在内层区域，满足内层问题：

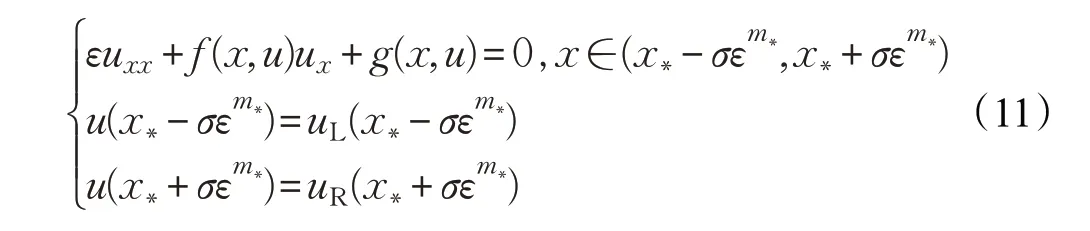
其中，uL(x)和uR(x)分别记为退化问题（9）和（10）的解。

对内层问题（11）引入拉伸变换x=x∗+σεm∗η，η∈[-1,1]，并且定义下列函数：

结合式（8），内层问题（11）转化为如下边值问题：

令ε→0，得到内层问题的近似：

随后，将通过求解该近似问题来确定宽度系数σ。

3.2 宽度估计及离散格式

本节采用RSCM对问题（13）进行离散，同时给出宽度系数σ的一个数值估计。

首先，建立一阶和二阶微分矩阵的分块形式：

由矩阵和向量的运算性质，得到问题（13）的离散形式：

其中算子“∘”表示矩阵的哈达玛（Hadamard）积。

需要指出的是，H͂是一个不仅与未知量u͂2有关，还与宽度系数σ有关的系数矩阵。因此，方程组（15）所含未知量的个数大于方程的个数，是一个不定问题。

为了确定宽度系数σ，同时求得内层问题的数值解，本文基于内层区域和外部区域连接端点处的一阶导数连续性条件，构造如下优化问题：

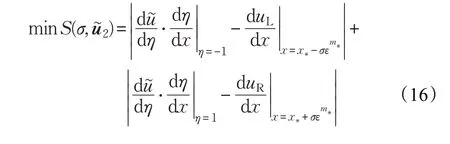
优化问题（16）的离散形式与代数方程组（15）构成一个以u͂2与σ为未知量的非线性方程组，这里通过Matlab优化工具箱中非线性方程求解器fsolve来进行计算，其本质原理是最小二乘法。在实际操作中，迭代初始值可以取为边界条件的线性插值。

将求得的最优宽度系数σ∗与式（8）确定的m∗代入宽度公式d=，至此便得到了内层宽度的估计值。为了进一步提高计算精度，可以将m∗及σ∗代入退化问题（9）、（10）和内层问题（12），采用RSCM进行离散求解，得到更高精度的数值解。

4 一类非线性奇异摄动问题的线性化求解

对于非线性问题，通常需要选取合适的迭代法进行求解。当方程的非线性项比较复杂时，牛顿迭代等一些经典格式的求解效果往往不理想，更不用提问题本身还具有奇性。本文引入文献[20-21]提出的Adomian分解法将非线性方程进行线性化。由数值实验可以得到验证，该线性化方法对奇异摄动问题的求解是行之有效的。

以如下一类非线性两点边值问题为模型介绍Adomian分解法：

记un-1(n≥2)为第n-1层迭代得到的数值解。在第n层上，对未知函数un进行分解：

同时，导函数有如下分解：

将式（18）～（20）代入模型问题（17），整理得到v0,1,2,3分别满足下列问题：

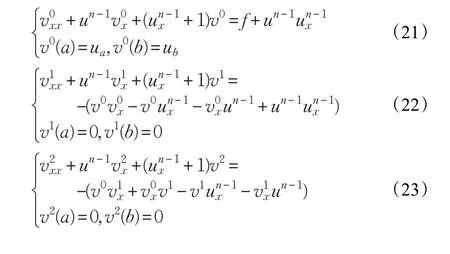
注意到un-1是已知的，因此方程（21）～（24）是线性问题，可以直接采用RSCM离散求得v0,1,2,3，代入式（18）得到un。当相邻两层迭代得到的数值解满足给定的容忍误差＜Tol时，计算终止。

现将Adomian分解线性化迭代算法的求解过程做如下整理：

步骤2当n≥1时，采用RSCM依次离散求解线性方程（21）～（24）得到v0,1,2,3，其中各方程所涉及的导数项可以由式（5）计算得到。将v0,1,2,3代入式（18）得到un。

5 数值实验

本文给出两个算例，来验证数值估计方法的可行性和有效性。算法通过Matlab软件实现，计算机的运行环境为Intel®CoreTMi5-6500 CPU 3.20 GHz，4.0 GB，Windows7（x64）。

例1考虑线性问题[22]：

具有精确解：

其中，erf(x)为剩余误差函数，δ=1/2ε。

根据奇异摄动渐近理论，该问题的解在x=0的小邻域内出现奇性层，不妨假设内层区域为[-σεm,σεm]。

首先，借鉴量纲分析方法确定m∗。对控制方程引入拉伸变换x=εmξ，转化为：

取1-2m=0，得到m∗=1/2，即内层宽度为d=2σε。

随后，将原问题分解为[-1,-σε]和[σε,1]上的退化问题，以及[-σε,σε]上的内层问题。采用第3.2节提出的宽度估计方法与RSCM结合进行离散求解。

取ε=10-3,10-4,…,10-9进行计算，每个区间上离散节点数N=30。由优化问题（16），求得最优宽度系数σ∗=4.5。表1通过枚举法列出了对应不同的ε值，当1≤σ≤7时，RSCM求得的离散节点上的最大误差。对比这些数值结果，可以发现当4≤σ≤6时，RSCM对所有的ε值都得到了比较理想的计算精度，并且精度值稳定。而远离该区间的σ值，计算误差逐步增大，本文方法求得的σ∗=4.5落在该区间内，验证了其合理性和有效性，避免采用枚举法或试错法产生的大量计算时间的浪费。图1刻画了ε=10-3,10-4,10-5时RSCM求得的数值解，可以看出解的变化趋势与估计得到的内层宽度是相互吻合的。

表1 例1中ε、σ取不同值RSCM计算得到的最大误差

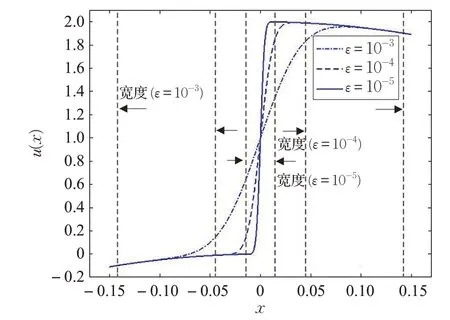
图1 例1中ε=10-3,10-4,10-5时的数值解及内层宽度

例2考虑如下非线性奇异摄动问题：

具有精确解：

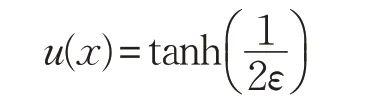
由渐近理论分析得到，该问题的解在x=0的小邻域内出现奇性层，不妨假设内层区域为[-σεm,σεm]。

首先，借鉴量纲分析方法确定m∗。对控制方程引入拉伸变换x=εmξ，转化为：

取m-1=0，得到m∗=1，即内层宽度为d=2σε。原问题相应地分解为[-1,-σε]和[σε,1]上的退化问题，以及[-σε,σε]上的内层问题。

本算例中考查ε=10-3,10-4,10-5时的数值求解，每个区间上取离散节点数N=50。由优化问题（16）求得最优宽度系数σ∗=8.2。进一步，结合第4章介绍的Adomian分解法迭代计算求得数值解，其中容忍误差Tol=10-8。表2通过枚举法列出了5≤σ≤13时，RSCM计算得到的最大误差。观察发现当7≤σ≤10时，RSCM得到的计算精度较优，并且稳定在10-4～10-5，本文方法得到的σ∗=8.2落在该区间内。当σ落在区间外部时，误差逐渐增大。当σ≥13时，甚至出现计算不收敛现象。由此可见，内层宽度的估计是否合理对非线性奇异摄动问题的求解起着至关重要的作用。此外，图2刻画了ε=10-3,10-4,10-5时，RSCM求得的数值解及估计出的内层宽度。这些数值结果说明了本文提出的数值方法对非线性问题也是有效的，同时得到了不错的计算精度。

表2 例2中ε、σ取不同值RSCM计算得到的最大误差

图2 例2中ε=10-3,10-4,10-5时的数值解及内层宽度

6 结束语

本文考虑了奇异摄动内层问题的数值计算，提出了一种内层宽度的估计方法。首先，将原问题依据内层区域和区域外部相应地分解为内层问题和退化问题两部分。随后，构造了一个非线性优化问题来确定宽度系数。采用重心形式的有理谱配点法进行离散求解。对一类非线性奇异摄动问题，引入Adomian分解法进行线性化迭代计算。数值实验表明，本文提出的方法对线性和非线性问题都是可行的，切实有效地给出了内层宽度的一个合理估计，数值解也达到了不错的计算精度。相比依赖人为经验的试错法或是枚举法，避免了大量计算时间的耗费，更是一种经济的数值方法。值得一提的是，本文的数值方法可以直接应用于边界层问题的计算。

目前，奇异摄动问题的数值解法还有许多问题值得深入研究。例如，求解区域上存在多个奇性层以及高维问题，这些都需要对本文方法进行不断改进，以适应求解各种不同类型的奇性问题。本文提出的内层宽度估计方法及实验结果，能为奇异摄动问题的理论分析及其数值计算的发展提供一臂之力。