格构梁锚杆加固滑坡地震动力响应分析

雷晓锋，汪班桥，李 楠

(1.西安公路研究院，陕西 西安 710065；2.长安大学地质工程与测绘学院，陕西 西安 710054)

锚杆支护体系是一种主动柔性支护体系[1]。唐山大地震、日本Hanshin-Awaji地震和汶川地震的震害调查[2-4]结果均表明，各类锚固系统的抗震性能良好，基本未出现明显灾害。尤其是格构梁锚杆支护体系，在地震波激励作用下，锚杆—格构—边坡岩土体三者协调变形位移，共同抗震抗滑，震后锚固边坡稳定性良好。

学者们采用模型试验、数值模拟等方法，对格构梁锚固系统在地震激励作用下的动力特性及抗震机理做了大量研究[5-17]。董建华等[9]、朱彦鹏等[10]采用有限元软件ADINA建立了框架锚杆支护体系水平地震动力计算模型，对比分析了地震激励前后锚固体系的位移、应力、加速度及锚杆应变等动力响应，揭示了不同因素对锚固边坡地震响应的影响规律。叶帅华等[11]采用Geostudio数值模拟软件，构建了多级高边坡框架预应力锚杆支护体系地震动物理模型，分析了锚固系统的位移、速度、加速度、应力及锚杆应变随地震持时的响应特性。文畅平等[12]、杨果林等[13]以锚杆框架梁和重力式挡墙组合式护坡结构为研究对象，采用数值分析和振动台试验相互验证的方法，研究了汶川波激励下顺层岩质锚固边坡的动力响应。杨明等[14]针对高烈度地区的斜坡堆积体，采用拟静力法离心模型试验和数值模拟方法，对比研究了抗滑桩和抗滑桩联合框架锚杆的破坏模式、水平位移及抗震机理等。郝建斌等[15]、汪班桥等[16]、付晓等[17]采用大型振动台缩尺物理模型试验，以格构梁锚固系统为研究对象，揭示了不同地震波加速度峰值激励下，锚杆、格构梁及坡体的动力响应特征。

相对数值模拟，振动台试验的研究经费高、试验周期长，因而采用模型试验重现的格构梁锚固边坡地震动力响应研究较少；研究成果也集中在锚固系统的位移、加速度等动力响应方面，对不同量级作用下滑坡及锚杆连续响应过程的分析很少。

本项目选择土质滑坡作为研究对象，采用振动台物理模型试验，结合锚固体系的损伤破坏特征、加速度响应以及同列锚杆的应变反应对地震波作用下格构梁锚固系统的响应过程进行分析，并给出了高烈度地区的抗震设计建议。

1 振动台模型试验设计

振动台试验在西安建筑科技大学结构抗震试验室的1#台面进行，如图1所示。1#振动台水平双向两个自由度，最大位移±25 cm，台面尺寸4.1 m×4.1 m，工作频率范围0.1～50.0 Hz；最大加速度±1.5g。

图1 试验模型Fig.1 The test model

试验原型滑坡高7 m，锚杆布设间距为2.0 m×1.5 m。根据振动台的工作频段、承载能力等设定模型几何相似比为7∶1，坡高1 m，锚杆间距为0.29 m×0.22 m。

模型箱由角钢和厚1 cm的可透视有机玻璃板构成，箱体长、宽、高分别为2.05 m、1.50 m、1.30 m。边坡模型填筑前，在箱体底面铺粘一层碎石，以减少箱土接触面的相对位移；在箱体前后两侧分别粘贴5 cm厚的聚乙烯泡沫板以减小边界效应。

试验模型的滑床及滑体均采用西安地区的黄土分层夯筑而成，压实系数0.93，实际夯实后的土体重度18.9 kN/m3，含水率14.6%；滑带由铺设于滑床上一层厚2～3 mm的干细土模拟，反算得其黏聚力c为 5.5 kPa，内摩擦角φ为 19°。锚杆和格构是在几何相似比7∶1的基础上，按规范设计计算确定。锚杆类型为全长无黏结压力型锚杆，锚孔直径为2 cm，采用光面消除应力的Φ6 mm钢筋模拟杆体，2 cm厚的Q235圆环钢板，通过螺帽固定在端头模拟承载板，钢筋上涂抹凡士林后缠裹塑料胶带以实现锚筋与砂浆脱粘模拟全长无粘结特性。灌注砂浆配合比为水∶水泥∶细砂=40∶29∶145。格构梁的制作是通过浇筑绑扎好的铝筋笼(4Φ6)来完成，其中混凝土强度等级为C10，配合比为水∶水泥∶细砂∶细石=0.8∶1.0∶2.96∶3.76，截面尺寸为40 mm×50 mm。

1.1 测试方案

如图2所示，坡内(测点A1、A2、A3、A4、A5、A6)及坡表(测点A7、A8、A9、A10、A11)不同高度处共埋设11只加速度传感器，用以监测同一断面不同高程处锚固滑坡的加速度响应。振动台台面上安装1只加速度传感器作为激励控制。

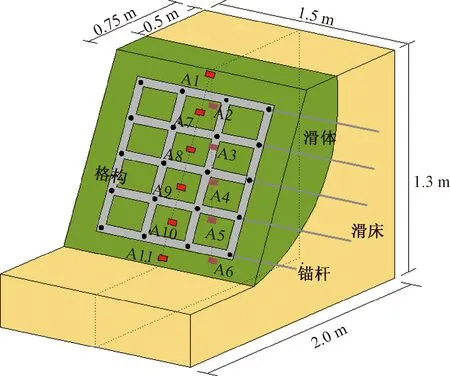
图2 三维模型示意图Fig.2 Schematic 3 D diagram of the model

为监测锚杆的应变响应，锚杆的杆身黏贴4只应变片(BE-120)，具体位置如图3。

图3 单根锚杆应变片位置图Fig.3 Layout of the strain gauges on the single anchor

1.2 加载方案

试验激励地震波单向水平输入，主要是因为水平地震作用是造成锚固系统损伤、降低边坡整体稳定性的主要因素[18]。试验激励波有三种：2008年四川汶川地震的汶川波(8.0级)、1940年美国Imperial Valley地震(6.9级)的EL Centro 波以及正弦波。正弦波采用定频输入，输入频率分别为5 Hz、10 Hz及15 Hz。

试验采用逐级施加地震加速度的方式进行，加载量级依次为0.05g、0.10g、0.15g、0.20g、0.30g、0.40g、0.60g、0.80g、1.00g，且在每次加载前输入平宽谱0.035g的白噪声扫描。试验中同列传感器的共振频率相差不大，取其平均值作为锚固系统的自振频率，如图4所示。

图4 同列传感器平均自振频率随加载量级的变化曲线Fig.4 Changes in the average natural frequency of the same column sensor in different stages of the test

2 锚固滑坡动力响应过程分析

图5为El Centro波激励下坡内同列各测点(A1、A2、A3、A4、A5、A6)PGA放大系数(测点PGA与台面PGA的比值)随激励强度的变化曲线。对比分析图4与图5可知，El Centro波激励下各测点加速度响应随加载强度的变化与自振频率随加载历史的变化趋势相同，分为三个阶段：0.05g～0.20g，曲线下降；0.20g～0.40g，曲线平缓；0.40g～0.60g，曲线上升。

图5 El Centro波激励下同列传感器PGA放大系数随加载强度的变化Fig.5 Variation in the PGA amplification coefficient of the same column sensor with the loading magnitude under the El Centro wave

图6为El Centro波激励下第三列各层锚杆平均应变随加载强度的变化曲线。和同列传感器PGA放大系数的动态响应过程一致，同列锚杆平均应变的动态反应也分为三个阶段：0.05g～0.20g，曲线密集紧凑，各层应变相差不大；0.20g～0.40g，曲线抬升明显，各层应变大小的顺序在调整变化；0.40g～0.60g，曲线平缓，但顶层锚杆M1-2反应激烈。

结合锚固滑坡模型试验素描图(图7)可知，小量级地震激励作用下(0.05g～0.20g)，振幅较小，类同于静载作用下锚固滑坡的受力，坡脚滑面附近首先出现剪切裂缝CD(0.15g)，并向两侧不断延伸；各层锚杆应变较小，其主动抗滑作用还没有发挥出来，滑体较滑床更为松散，模型土体的抗剪强度及剪切模量逐渐减小，土体水平剪切作用自下而上的传播速度降低，系统的自振频率有所下降，测点PGA放大系数减小。

激励强度增大至中等0.20g～0.40g，坡脚的剪切口裂缝不断向内延伸并变宽，坡顶预设滑面附近开始出现一些与预设滑面走向相近的裂纹，第二层锚杆下方的传感器A3-2附近出现第二个剪出口JI(0.40g)，但还没有和预设滑面贯通。此激励量级阶段，格构梁锚固体内部裂缝的不断发展，充分调动了锚杆的主动抗震抗滑性能，各层锚杆应变不断抬升，不断调整，且由于第二个剪出口JI的出现，坡顶第一层锚杆(M1-2)的应变最大，第二个剪出口附近的第三层锚杆(M3-2)应变次之。滑体—滑床—锚杆—格构梁形成一个整体，锚固系统的自振频率不再下降，测点的PGA放大系数缓慢增长，曲线分布相对平缓。

高量级地震波(0.40g～0.60g)激励作用时，锚固体的上下剪切裂缝均贯通，裂缝宽度越来越大，破损越来越明显，模型滑坡体的自振频率虽还有增长，但已经非常平缓。第二个剪出口JI和贯通后的预设滑面相连，形成明显的拉裂体FGHIJ，坡顶的滑体与滑床分离现象明显，传感器 A1和A2的PGA放大系数相对增长更为明显；振动过程中明显可见滑面处的裂缝越来越宽，滑体与滑床的动位移越来越不协调，锚固体的动态响应越来越强烈，各层加速度传感器的PGA曲线整体抬升；各层锚杆受力最终调整为第一层(顶层)>第五层(底层)>第三层>第四层>第二层，且顶层受力随加载强度增加而增大的趋势越来越明显，其他四层则趋于稳定。

对各区段动力响应的特征进行分析可知，小量级激励作用下，锚固体的动力响应类同于静载作用；中量级激励时则开始发挥出其主动抗滑抗震的性能；高量级激励时锚固滑坡并未发生整体失稳破坏，这种协调变形、延时破坏的能力表现更加明显。基于各区段的不同表现，将其分别命名为：适应调整区段(0.05g～0.20g)—平和抗震区段(0.20g～0.40g)—激烈抗震区段(0.40g～0.60g)。

为更加明确地震波激励下锚固滑坡体的动力反应及损伤特征，对正弦波定频(5 Hz、10 Hz 、15 Hz)、El Centro波、汶川波激励作用下各层锚杆的动态响应进行对比分析。

3 不同激励作用下同列锚杆应变对比分析

图8为正弦波(5 Hz、10 Hz 、15Hz)、El Centro波及汶川波激励作用下同列锚杆平均应变曲线随加载量级的变化曲线，第一行为初始低量级(0.05g～0.20g)加载，第二行为中高量级(0.20g～0.60g)加载。和第2节加速度响应过程吻合，同列锚杆应变随加载强度的变化也可分为三个区段：适应调整区段(0.05g～0.20g)—平和抗震区段(0.20g～0.40g)—激烈抗震区段(0.40g～0.60g)。

图8 不同激励作用下同列锚杆应变曲线Fig.8 Strain curve of the same row bolt under different excitations

适应调整区段(0.05g～0.20g)：除正弦波15 Hz定频激励作用，在其它激励作用下，各层锚杆的应变曲线均呈现上小下大的“L”型，坡脚锚杆的应变绝对大于其余各层的动应变；与这一激励量级下锚固体的自振频率及同列测点的动力响应相吻合，锚固系统的整体抗震抗滑作用尚未发挥出来。锚固滑坡在这一量级的动力响应与静载作用时相同，地震激励所产生的动荷载主要由坡脚锚杆M5-3承担。

水平地震激励作用下的锚固体如同来回筛动的筛子，15 Hz接近锚固体的自振频率，在锚固体上产生不协调变形较大，尤其是锚固体上部。为抑制滑坡上部的不协调变形及坡脚的剪切裂缝，顶层锚杆和坡脚锚杆的应变相对中部较大，同列锚杆的应变振型呈现中间小上下大的“C”型。

平和抗震区段(0.20g～0.40g)：5 Hz地震波激励下，各测点的应变响应随加载量级的增加而增长，同列锚杆的平均应变曲线保持“L”型不变，坡脚锚杆M5-3应变增长最为迅速。

15 Hz地震波激励下，锚杆的主动抗滑抗震性能充分发挥，坡体内部各层传感器的动态响应发展平稳，各层锚杆不断增长的应变分担了不断增大的地震激励；各层锚杆承担的应变大小不断变化、分配，为平衡中等量级范围时坡顶滑面处不断发展、贯通的裂缝(图7)，顶层锚杆M1-3的应变要远远大于其余几层锚杆，曲线调整为明显的“Г”型。10 Hz地震激励作用下，同列各层锚杆的应变分部曲线依然保持明显的 “C”型。

El Centro波激励作用下同列锚杆的应变振型与5 Hz正弦波的振型一致，上小下大“L”型；汶川波激励作用下同列锚杆的应变振型则与10 Hz正弦波的振型一致，坡顶与坡脚的应变明显大于坡体中间，呈现出明显的 “C”型。

激烈抗震区段(0.40g～0.60g)：这一量级作用下同列锚杆的应变振型和中等量级作用下基本一致。但由于0.60g时坡脚剪切裂缝CDEAOB(图7)贯通，坡脚首先进入弹塑性区，一定程度上减小了坡脚处的锚固力， 各激励作用下锚杆M5-3的应变均有所减小。

0.60g之后，为观察锚固系统的破坏过程，只对模型进行了低频5 Hz的地震激励。

强震低频(0.80g，5 Hz)作用下，坡顶拉裂体FGHIJ(图7)形成，滑体与滑床筛动位移增大，滑面处的裂缝也随之变宽，尤其是坡顶附近，为抑制两者之间的不协调位移，同列锚杆的拉力再次重新调整、分配， M1-3、M2-3的应变急剧增大；整个应变曲线呈现明显的阶梯状，上大下小。1.0g时，锚杆上应变急剧增加，大部分测点已无数据；格构梁锚固体内部稳定完整，但没有锚固的素土区及坡顶发生崩裂破坏。

由此可见，同列锚杆的大应变区集中在坡脚和坡顶两个位置，且和激励作用的频率有关，而实际的地震激励波由于综合了大大小小不同的频谱，坡顶和坡脚的应变反应均较大，同列锚杆的应变走势呈现“C”型。这不仅对原有“强腰固脚”的抗震设计提出疑义，也要求抗震设计过程中加强坡顶及坡脚的防护工作。

4 结论及建议

本项目在土质滑坡振动台物理模型试验的基础上，研究了格构梁锚固系统的动态响应过程，结果表明：随着地震激励强度的增加，土质滑坡锚固体系的自振频率和动力响应也在变化，主动抗滑抗震的锚杆受力也随着调整、协调，以抑制动力作用下锚固滑坡上的拉压变形。

(1)地震激励作用下，锚固体的动力响应分为三个阶段：适应调整区段(0.05g～0.20g)—平和抗震区段(0.20g～0.40g)—激烈抗震区段(0.40g～0.60g)。

(2)适应调整区段(0.05g～0.20g)，激励强度较小，锚固系统的自振频率和PGA放大系数随着加载强度的增大略有减小；自振频率附近的激励强度由于共振作用，在锚固体上部产生的不协调变形较大，同列锚杆的应变走势呈现“C”型；其它激励作用下同列锚杆的应变曲线均呈现上小下大的走势，地震激励所产生的动荷载主要由坡脚最下层锚杆承担。

(3)平和抗震区段(0.20g～0.40g)，锚固滑坡—锚杆—格构梁形成一个整体，共同抗震抗滑，整个系统的自振频率处于平稳水平；各层测点PGA放大系数及各层锚杆锚固力持续缓慢增长。不同激励作用的频谱不同，同列锚杆的应变振型亦不同，大致可分为上小下大的“L”型、上大下小的“Г”型及中间小上下大的“C”型。

(4)激烈抗震区段(0.40g～0.60g)，锚固系统自振频率有所抬升，主动抗震抗滑特性增强，锚固系统动力响应强烈。坡脚剪出口贯通，坡脚锚杆的应变有所下降，同列锚杆的应变振型保持不变。

(5)破坏过程中(0.60g～0.80g)，同列锚杆的应变振型发生明显变化，首先是坡脚锚杆的应变减小，其次是坡顶锚杆为抑制坡顶土体的拉张破坏应变而急剧增大。

(6)强震地区锚固系统设计时，需加强坡顶及坡脚的防护工作，同时加长设计坡顶与坡脚的锚杆，以抑制坡顶滑面处的拉张裂缝及坡脚的剪切裂缝。