考虑温度影响的改进西原流变模型及一维固结解

陈 航，刘干斌，郭 华，周 晔，吴章俨

(宁波大学岩土工程研究所，浙江 宁波 315211)

在核废料处理、地热开采、热力管线埋设、公共交通系统等诸多工程建设领域，温度对土体力学性质的影响受到越来越多的关注[1]。此外，大量工程也表明，软黏土具有显著的流变性[2]。因此国内外学者开展了诸多软黏土的流变试验、流变模型研究。例如郭华等[3-4]基于四元件流变模型，即是由一个弹性模量为E0的弹簧、一个黏滞系数为η0的黏壶和一个Kelvin体串联而成，考虑温度影响，建立了宁波软黏土流变固结模型，并在广义Merchant三元件模型基础上，引入温度膨胀系数，建立了饱和土体三元件热流变模型。杨超等[5]通过分别加载和分级加载2种方式进行了一维固结流变试验，研究了上海海相软土一维固结流变特性和计算模型。

由于西原模型能较好地模拟岩土的流变特征，近年来许多学者对西原模型进行了改进，例如郤保平等[6]从热力耦合作用下花岗岩的流变机制研究出发，建立热力耦合作用下花岗岩的流变模型。左建平等[7]作了热力耦合作用下岩石流变模型的本构研究，并基于西原流变模型得出热力耦合作用下西原模型的蠕变方程、卸载方程和松弛方程。张旭东[8]为探究软岩隧道围岩变形的蠕变时效性，采用非定常黏滞体对西原模型进行修正，分析了围岩黏弹性和塑性阶段隧道围岩变形过程，推导得到了隧道围岩黏弹塑性解。曹瑞琅等[9]将Hoek-Brown强度准则引入到西原流变本构模型，得到了支护条件下Hoek-Brown准则西原模型的圆形隧洞黏弹塑性解。邓宗伟等[10]基于土体流变特性，对西原模型低应力分量进行改进，即用Schiffman模型代替Merchant模型，得到瞬时加载下的改进西原模型一维固结解析解。齐亚静等[11]通过在西原模型上串联一个带应变触发的非线性黏壶，提出改进的西原模型，推导岩石在恒应力情况下的三维蠕变本构方程。阎岩等[12]在蠕变模型中考虑蠕变参数随应力、时间等因素而变化是解决非线性蠕变问题的方法之一。付腾飞等[13]在西原模型的基础上，引入Kachanow损伤理论及时间损伤阈值，建立了一种同时描述3个阶段的非线性损伤蠕变方程式。

本文考虑土体的黏弹塑性变形特性，引入膨胀系数，建立热力耦合的西原模型，推导了土体热流变固结方程，并求得了瞬时加载条件下一维热固结方程的解析解。

1 改进西原流变模型

1.1 西原模型

西原流变模型是1个Merchant模型串联1个Bingham体，如图1所示。Merchant模型由1个Hooke体和Kelvin体组成，即由1个黏滞系数为η1(T)的黏壶和1个弹性模量为E1并联后再串联1个弹性模量为E0的弹簧；Bingham体则由1个屈服应力为σs的塑性元件和1个黏滞系数为η2(T)的黏壶并联而成。西原模型将弹性体、黏性体、塑性体串联起来，能够描述土体黏弹塑性特性。

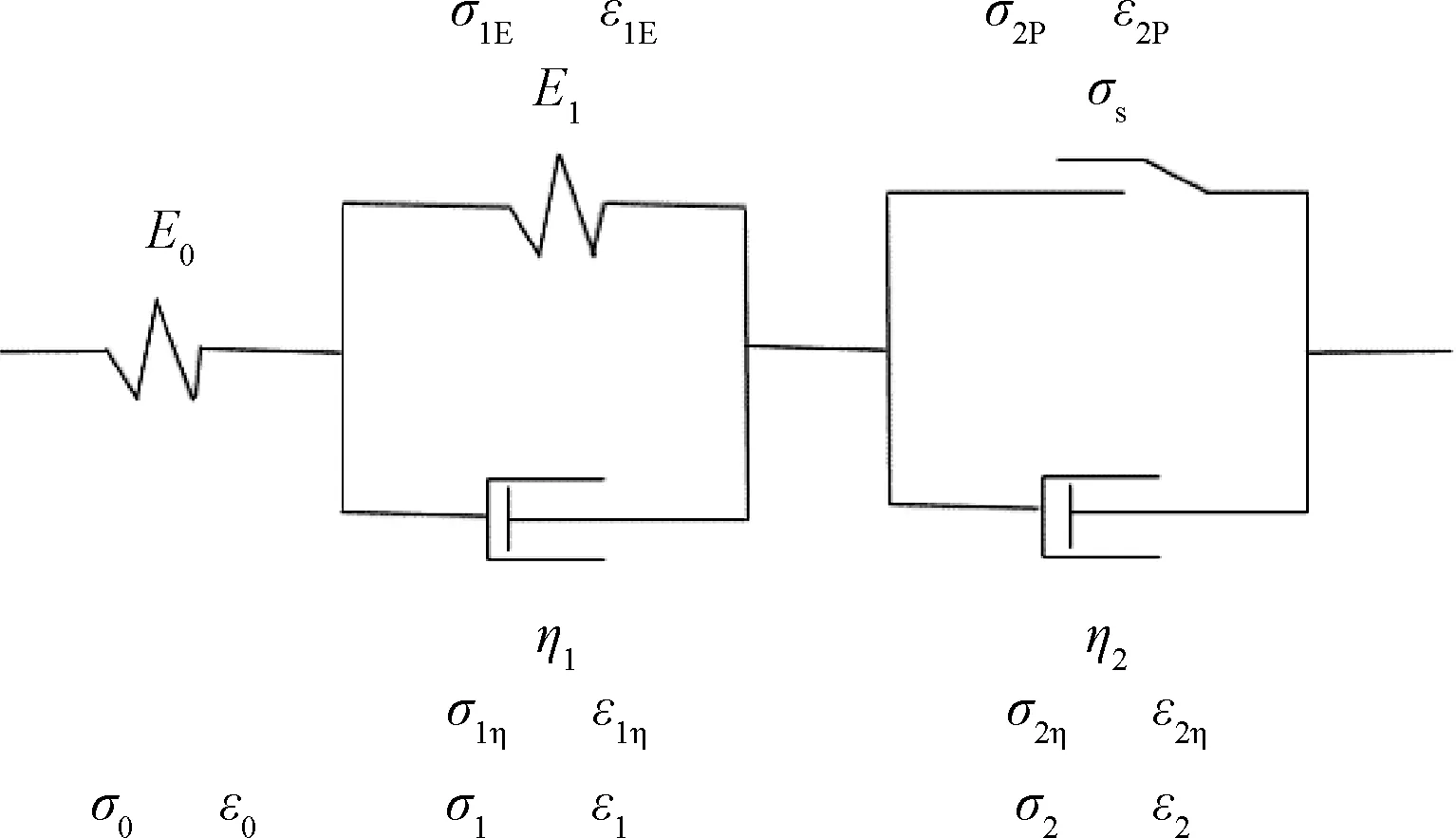
图1 西原流变模型Fig.1 The Nishihara rheological model

1.2 考虑温度影响的西原模型

假设饱和软黏土的有效应力为σ′，则西原模型的应力-应变关系如下：

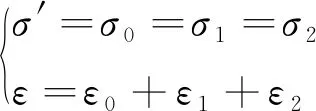
(1)

式中：σ′——有效应力；

σ0，σ1，σ2——Hooke体、Kelvin体和Bingham体的受到的应力；

ε——总应变；

ε1，ε2，ε3——Hooke体、Kelvin体和Bingham体的应变。

在热力耦合作用下西原模型中各元件的应力-应变关系为：

(2)

式中：ΔT——任意温度差，ΔT=T-T0，其中T0为初始温度；

E0，α0——第一个弹性元件的弹性模量和热膨胀系数；

E1，α1，σ1E，ε1E——Kelvin体中弹性元件的弹性模量、热膨胀系数、承受的应力和应变；

η1(T)，σs1n，ε1n——Kelvin体中黏性元件的黏滞系数、承受的应力、应变，η1(T)是与温度有关的常数；

η2(T)，σ2n，ε2n——Bingham体中黏性元件的黏滞系数、承受的应力、应变，η2(T)是与温度有关的常数；

σ2p，ε2p，σs——Bingham体中塑性元件承受的应力、应变和屈服极限。

当塑性元件承受的应力σ2p小于其极限屈服应力σs时，Bingham体中的塑性元件不发生作用，因此西原模型可简化为三元件模型；当塑性体承受的应力σ2p大于其极限屈服应力时，塑性元件承担的应力为σs。

若考虑土体的塑性变形时，基于上述模型可得土体的应力-应变关系为：

(3)

(4)

(5)

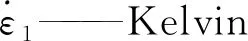
假设温度增量随时间线性变化，即ΔT=kt，其中k表示为温度随时间线性变化系数，k为常数，式(3)、式(4)可表示为：

(6)

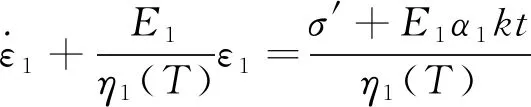
(7)

对式(5)和式(7)进行积分求解，可分别求得ε1、ε2：

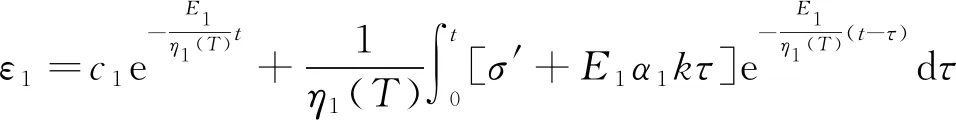
(8)

(9)

式中：c1，c2——系数。

由式(8)和式(9)可以得到考虑热力耦合的西原模型的总应变为：

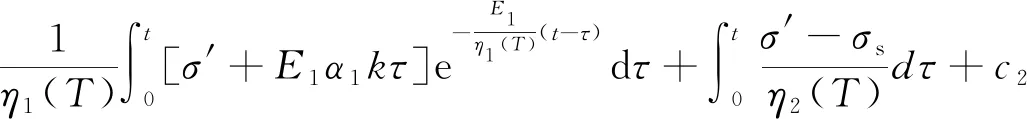
(10)

当t=0，即热力耦合西原模型中塑性元件不发生作用，且c1=c2=0时，模型只有弹性变形，考虑热力耦合西原模型式(10)可以退化为：

(11)

当c1=c2=0时考虑塑性变形的热力耦合西原模型的应力-应变关系可表示为：

(12)

若忽略温度影响，则式(12)退化为如下形式：

(13)

综上，式(13)即为考虑热力耦合作用的广义一维西原流变模型本构方程。

2 热力耦合流变固结问题

2.1 问题的描述

考虑单层地基的一维固结问题，如图2所示，假设软黏土表面排水，底面不排水，土体表面作用随时间变化的连续均布荷载为q(t)，瞬时加载下荷载简化为q0，kv是竖向渗透系数，软黏土层厚度为H，其他E0，η1(T)，E1，η2(T)，σs为流变模型参数。

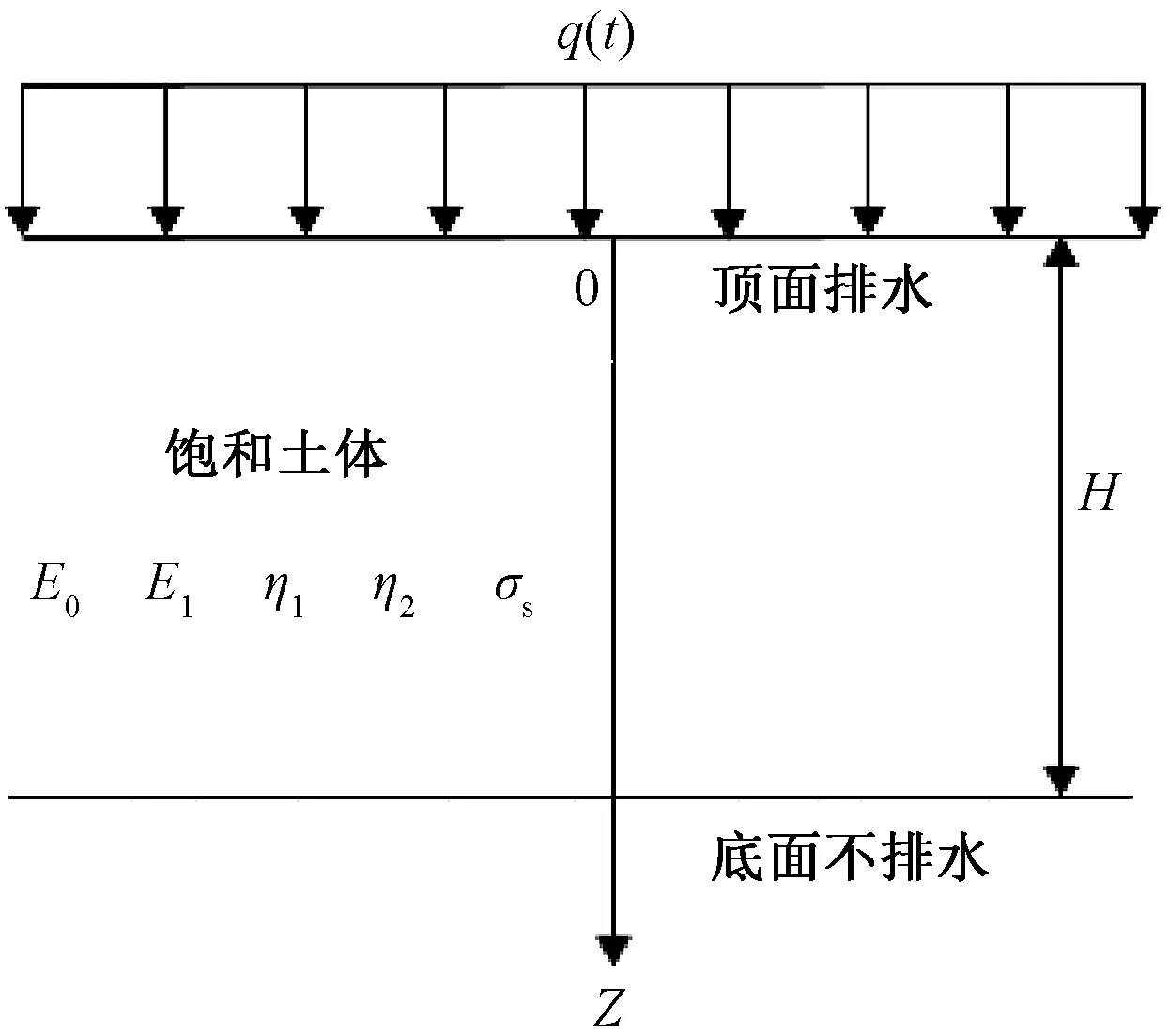
图2 单层地基固结问题Fig.2 Consolidation problem of a single layer

假设土体饱和且土颗粒和孔隙水均不可压缩，则单位时间内排出的水量和土骨架的压缩量相等，可得：

(14)

式中：kv——土体竖向渗透系数；

γw——土中水的重度。

根据土体有效应力原理：

σ′=q(t)-u

(15)

式中：q(t)——作用在土体上随时间变化的荷载；

u——孔隙水压力。

联立式(12)、式(14)和式(15)，得到饱和软黏土热力耦合作用下的黏弹塑性一维流变固结方程：

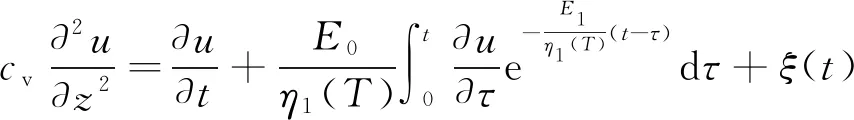
(16)

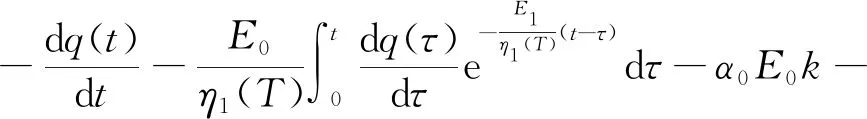
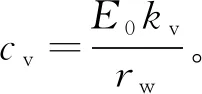
2.2 方程求解

考虑瞬时加载，q(t)=q0，则控制方程式(16)可表示为：

(17)

求解条件为：

边界条件：单面排水：u(0,t)=0，uz(H,t)=0；

初始条件：u(z,0)=q0

为求解式(17)，可设孔压u的表达式为：

(18)

式中：Tn(t)——时间t的一次函数。

将式(18)代入式(17)，可得：

(19)

对式(19)进行Laplace变换，可得：

(20)

由初始条件，可知：

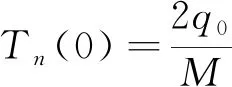
(21)

将式(21)代入式(20)，可得：

(22)

对式(22)进行Laplace逆变换，得：

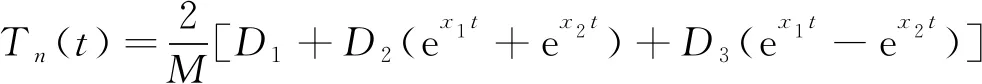
(23)

其中：

将式(23)代入式(18)，则孔压u的表达式可表示为：

(D2-D3)ex2t]

(24)

(D2+D3)ex1t+(D2-D3)ex2t]

(25)

在式(25)中用H/2代替H可以得到双面排水情况下即顶面和底面均排水时的孔压表达式。同理，也可以得到双面排水情况下的固结度表达式。

3 试验验证及结果分析

3.1 试验验证

为验证模型及理论结果的正确性，与尹铁锋等[14]热固结试验结果进行对比分析。在50，100，200 kPa围压和30，45，60，75 ℃条件下进行了12次温控等压固结试验，试验中待孔压稳定后将温度升至预定值，待孔压再次稳定后进行排水固结，期间测得孔压试验值，结果如图3所示。

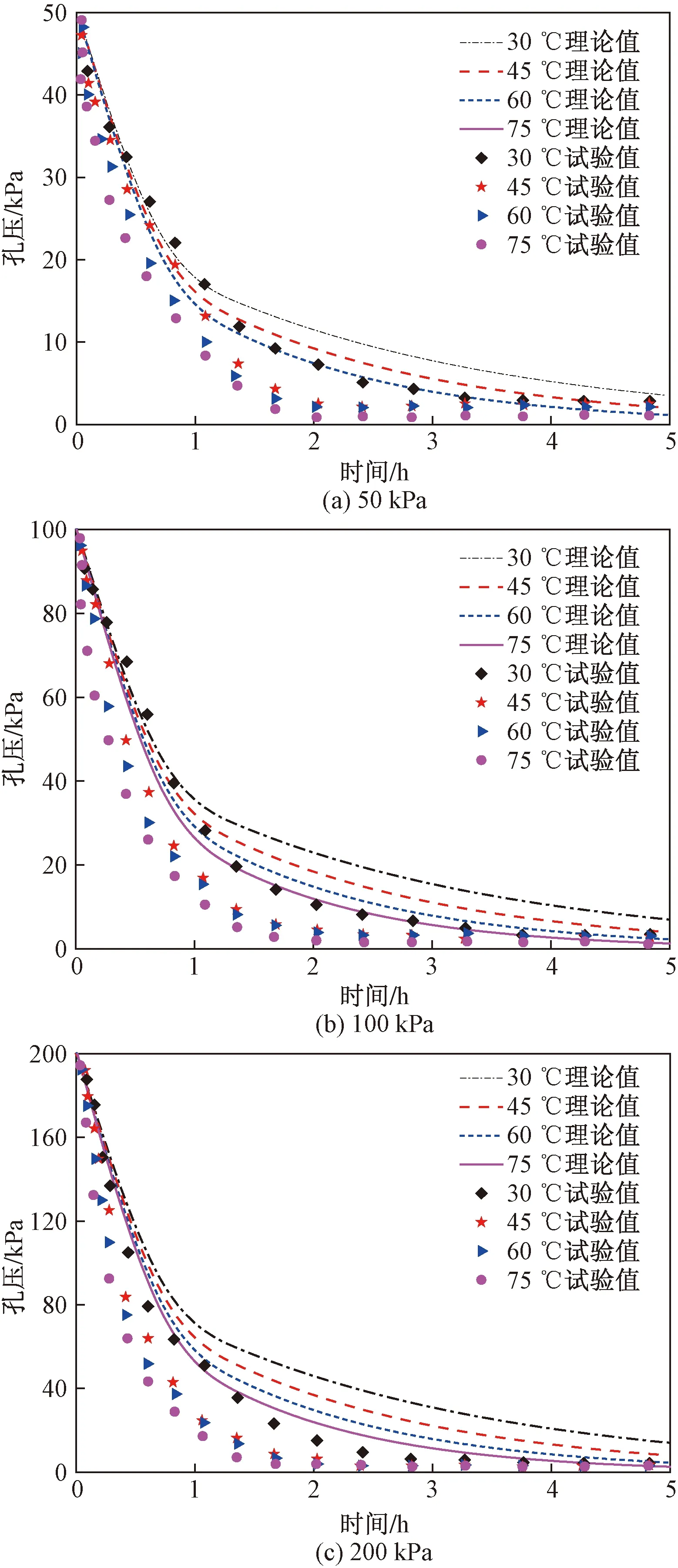
图3 不同温度下孔压试验和计算结果对比Fig.3 Pore pressure results for test and theory at different temperatures

为了与热固结试验结果进行对比，参考郭华等[4]、谢新宇等[15]、邓岳保等[16]有关宁波软土的流变研究结果，考虑温度影响改进西原流变模型的参数取值如下：kv=5.779×10-10m/s、E0=1.5×104kPa、E1=6 000 kPa、α0=1.5×10-5/℃、α1=2×10-5/℃；20 ℃下的黏滞系数η1=6.818×107kPa·s、η2=8×107kPa·s；H=0.08 m。根据邓宗伟等[10]取土体的屈服极限，即应力阈值σs=50 kPa。

当固结压力不大时，黏滞系数主要受温度影响[17]，张鸿雁等[18]研究表明，黏滞系数与温度的作用关系如下：

(26)

式中：ηT——不同温度下的黏滞系数；

ηR——常温时的黏滞系数。

由式(26)可以计算得到不同温度下的黏滞系数η1，η2，结果如表1。假设温度线性变化上升时间为105s，则当初始温度T0为20 ℃时，系数k的结果如表1所示。

表1 不同温度下的黏滞系数和系数k

利用Matlab编程，计算得到不同温度和固结压力下的孔压，结果亦列于图3中。试验和理论计算结果均表明：在固结压力一定时，随着温度的升高，不同时刻的孔压有明显的减小，说明温度可以影响到土体的排水效果，其原因主要系温度升高，使得饱和土中水的黏滞系数减小，渗透系数增大，孔隙水加速排出，土体固结速率增大。此外，试验采用三轴试样，体积较小，利于排水，试验得到的孔压消散速度大于理论计算值。

3.2 温度对固结度的影响

由于温度对土体的孔压消散有较大的影响，为更直观地反映温度对土体固结速度的影响，对不同温度和压力作用下的固结度进行计算，结果如图4和图5所示。从图4中可以看出，随着温度的增加，土体中的孔压消散越快，土体固结越快；加温和加载初期，土体的固结速率较快，随后逐渐减小。由图5可以看出，不同压力作用下，土体平均固结度基本相同，平均固结度不受固结压力的影响。

图4 温度对固结度的影响(100 kPa)Fig.4 Effect of temperatures on degree of consolidation (100 kPa)

图5 地表压力对固结度的影响(60 ℃)Fig.5 Effect of surface pressures on pore pressure (60 ℃)

3.3 流变模型参数的影响

(1)弹性模量

为分析弹性模量对土体固结特性的影响，取E0和E1值如表2所示。当弹性模量增大时，饱和土的孔隙水会加速排出，孔压消散速率大、固结速度加快(图6)。

表2 E0、E1取值

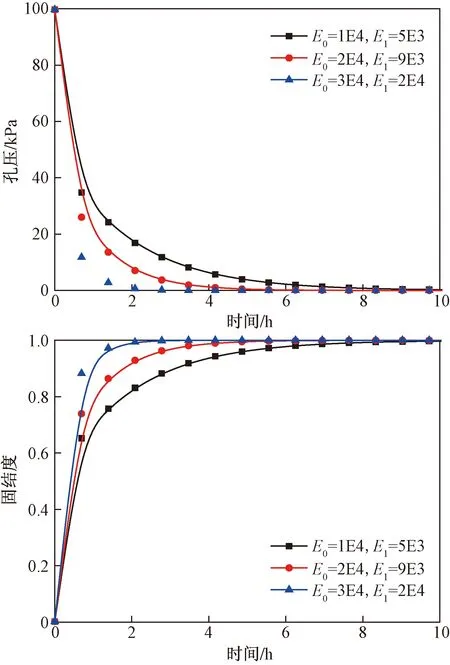
图6 弹性模量对孔压和固结度的影响(60 ℃,100 kPa)Fig.6 Effect of elastic modulus on pore pressure and degree of consolidation (60 ℃, 100 kPa)

(2)膨胀系数

土颗粒的膨胀作用由弹簧的膨胀系数来描述，为分析膨胀系数对土体热固结的影响，选择3组膨胀系数(表3)，计算结果如图7所示。可以看出，膨胀系数对土体孔压消散和固结度影响很小，说明土颗粒受温度影响而产生的热膨胀对于土体热固结孔压消散的作用非常小，可忽略不计。

(3)黏滞系数

为了分析Kelvin体中黏壶和塑性元件中黏壶的黏滞系数对土体固结速度的影响，对η1和η2分别取值，如表4所示，计算得到不同黏滞系数时的孔压和平均固结度结果如图8所示，可以看出黏滞系数越小，孔压消散越快，土体固结越快。

表3 不同α0和α1值

表4 不同η1和η2值

4 结论

从黏弹塑性角度出发，在西原模型基础上，考虑膨胀系数和黏滞系数的温度影响，建立了考虑热力耦合的改进西原模型，求解了一维热固结方程，主要结论如下：

(1) 温度升高可导致黏滞系数减小，渗透系数增大，孔隙水消散速率加快，土体固结加快。

图7 膨胀系数对孔压和固结度的影响(60 ℃,100 kPa)Fig.7 Effect of the expansion coefficient on pore pressure and degree of consolidation (60 ℃, 100 kPa)

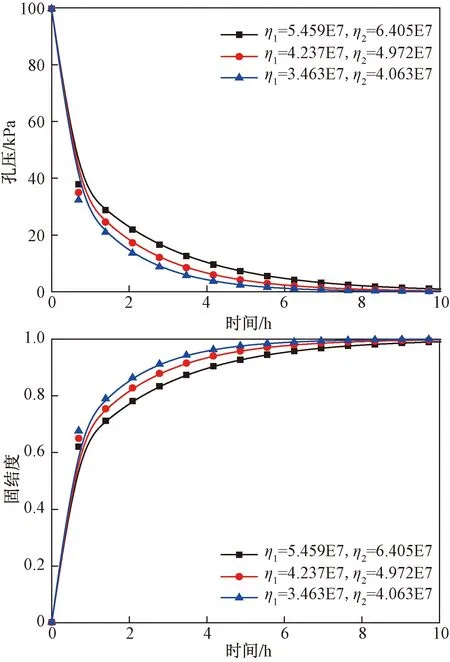
图8 黏滞系数对孔压和固结度的影响(60 ℃,100 kPa)Fig.8 Effect of the viscosity coefficient on pore pressure and degree of consolidation (60 ℃,100 kPa)

(2)改进西原模型的弹性模量越大，孔压消散速率大，土体固结越快。土颗粒受温度影响而产生的热膨胀对于土体热固结孔压消散的作用非常小。黏滞系数越小，孔压消散越快，土体固结越快。

(3) 试验结果与考虑土体的黏弹塑性的热力耦合改进西原模型计算结果吻合，改进西原模型可以较好地描述土体的热力耦合特性。