郑州地下水均衡试验场的改建工程
——试验场监测资料的推广应用核心问题
乔晓英,肖 平,王继华,李俊亭,王 林
(1.长安大学水利与环境学院,陕西 西安 710054;2.干旱区地下水文与生态效应教育部重点实验室,陕西 西安 710054;3.河南省地质环境监测院,河南 郑州 450016)
国际、国内已经建立了多个包气带—地下水系统原位监测与试验基地[1],例如加拿大Borden 场地[2],美国MADE 试验场[3]、Hanford 场地[4]、德国的Krauthausen场地[5],国内武汉大学建立的大型蒸渗仪系统[6]、长安大学在渭河关中平原和鄂尔多斯风沙滩地建成的多功能地表—地下水原位试验基地、中国科学院禹城综合试验站、中国地质科学院水文地质与环境地质研究所衡水原位试验场等[7],实现了对地表—地下水系统状态变量实时监测,为开展多尺度地下水文过程的机理研究提供了基础[8]。
河南省郑州地下水原位试验场改建后,成为国内设备较全、观测数据类较多、数据采集自动化程度较高的原位试验场之一。其最大特点是试验柱中的组合岩性,是依据河南省五个地貌单元典型剖面经专家概化后的非均质岩性仿真而构成,经过实时监测,可获得试验场尺度下充水(降雨入渗)与释水(潜水蒸发)水文过程、13种典型岩性水分特征曲线,继而构建降水入渗或潜水蒸发预报联合模型[9]。但实际应用中如何将所建场地尺度模型推广应用于复杂的野外状况,探求天然状态下潜水面、包气带介质对大气降水与蒸发(腾)的响应机制,是水文地质环境地质工作者长期面临的难题之一,其核心问题是包气带参数的空间变异问题。本文试图探讨一种有较高精度的大气降水对地下水补给与潜水蒸发影响的评估方法,对于正确评估黄河冲积平原地下水资源的可持续开采与生态环境保护有重要的理论与实践意义。
1 郑州地下水均衡试验场数据监测成果
原郑州地下水均衡试验场始建于1981年,1983年开始监测。试验柱是地下水均衡试验场的核心构筑物[10]。改建后的试验柱介质来自黄河北冲积平原、黄河南冲积平原、淮河冲积平原、南阳盆地、豫西黄土丘陵等五个地貌单元的包气带(约7 m深度)岩性及其迭置关系,共计25个试验柱,仍采用原有地下水位埋深,分别为1,2,3,5,7 m五种深度。每个试验柱都设计有独立供水系统,以保证“水位控制埋深线”处的水均衡。试验柱亦呈环形布置,放置在以排气通道为中心5个地下监测室中,共安装设置了140个土壤负压传感器[11-12],140个土壤含水率与温度传感器。针对郑州地下水均衡试验场周边高楼林立,失去了应用气象部门信息的可能。因而安装了3 m高主杆的HOBO野外气象站。采用U30-NRC采集器,采集间隔最小可自定义为1 s,另外还有2套自行建立蒸发(含降水)对比试验观测。一套是E—601,另一套是自行设计的双圈水面蒸发筒[13-14]。
2 均衡试验场与野外现场的包气带建模方法对比
首先是研究目的各不相同。前者是结合拟解决的实际问题,比如针对包气带的多层结构,探讨包气带在某些特定条件下的水分运移规律;后者则是解决区域潜水面蒸发与入渗量等实际问题。因而前者是研究基础,后者是研究目标。二者最大差别是包气带参数的选取和土质结构的不同。在试验场尺度下,试验土柱岩性结构是仿真了野外实际条件,单就某一层来讲是均一的。根据试验柱中观测数据(含水率、负压、温度)确定的参数可能与野外实际(按颗分结果分类定名的同一岩性)参数值有较大的差异。这种差异主要来源于包气带土质沉积过程(沉积环境)的随机性,诸如沉积过程中水流速度、水中泥沙结构及影响沉积过程的其他自然环境等因素。因而实际上对于同一种岩性参数来说,在时空分布上也会有变异。二者相同之处在于构建的数学模型、边界条件基本一致,初始条件的确定需结合野外条件选择有所不同。国内曾在河南省商丘大吴庄进行过较大地块(长70 m、宽40 m)参数变异性研究,研究目标是土壤,取样深度最大也只有40 cm[15]。其研究结论对于解决区域性(千米级)包气带参数变异性问题具有一定的参考价值。本次研究侧重于模型的空间尺度、原状土样测试、包气带参数个数等方面做进一步改进。

图1 改建后的郑州地下水均衡试验场俯视图[6]Fig.1 Top view of the Zhengzhou groundwater balance experiment site after reconstruction
从均衡试验场监测成果到实际应用,不可回避的核心技术是区域条件下包气带参数的变异性问题。国际学术界自20世纪70年代提出包气带物理参数的空间变异性以来,多数学者认为,包气带参数变异性是指包气带介质的物理参数变异是空间的函数[15],而同一岩性在不同深度的物理参数变异则是时间的函数。以往土壤特性空间变异性研究基于观测或取样资料,分析土壤各特性参数的空间变化特征、参数间的空间关系,以确定合理的取样点数目,从而对未测点的参数进行最优估值等。进一步结合标定理论的应用来分析和预测状态变量的空间分布[16]。例如在欧美国家,基本上是采用野外采样,通过室内试验测试包气带物理参数,建立仿真大气降水与蒸发(腾)数学模型,预测大气降水对地下水的补给与蒸发(腾)。这种方法理论严谨,但还是没有突破需要现场参数测试的局限,因而解决实际问题尚有一定差距。而且研究成果多集中在表层土壤水分的空间结构分析,对包气带剖面土壤水分的空间结构特性研究不足,缺乏系统分析实测土壤水分空间结构变化规律的实际应用[9]。
3 包气带参数变异性研究思路与方法
针对包气带参数变异性问题,笔者认为有两种研究思路可借鉴:(1)用概率模型表述;(2)数学地质模型表述。基于此,本文试图通过原状土采样、分析测试、数学建模等手段,探讨均衡试验场监测数据推广到实际应用的一种方法(图2)。其中,构建包气带野外参数模型是关键步骤,包括按照一定精度和置信水平,确定取样数目;根据半方差和自相关图分析土壤特性的空间结构(方向性和相关距离);应用Kriging法进行内插计算。
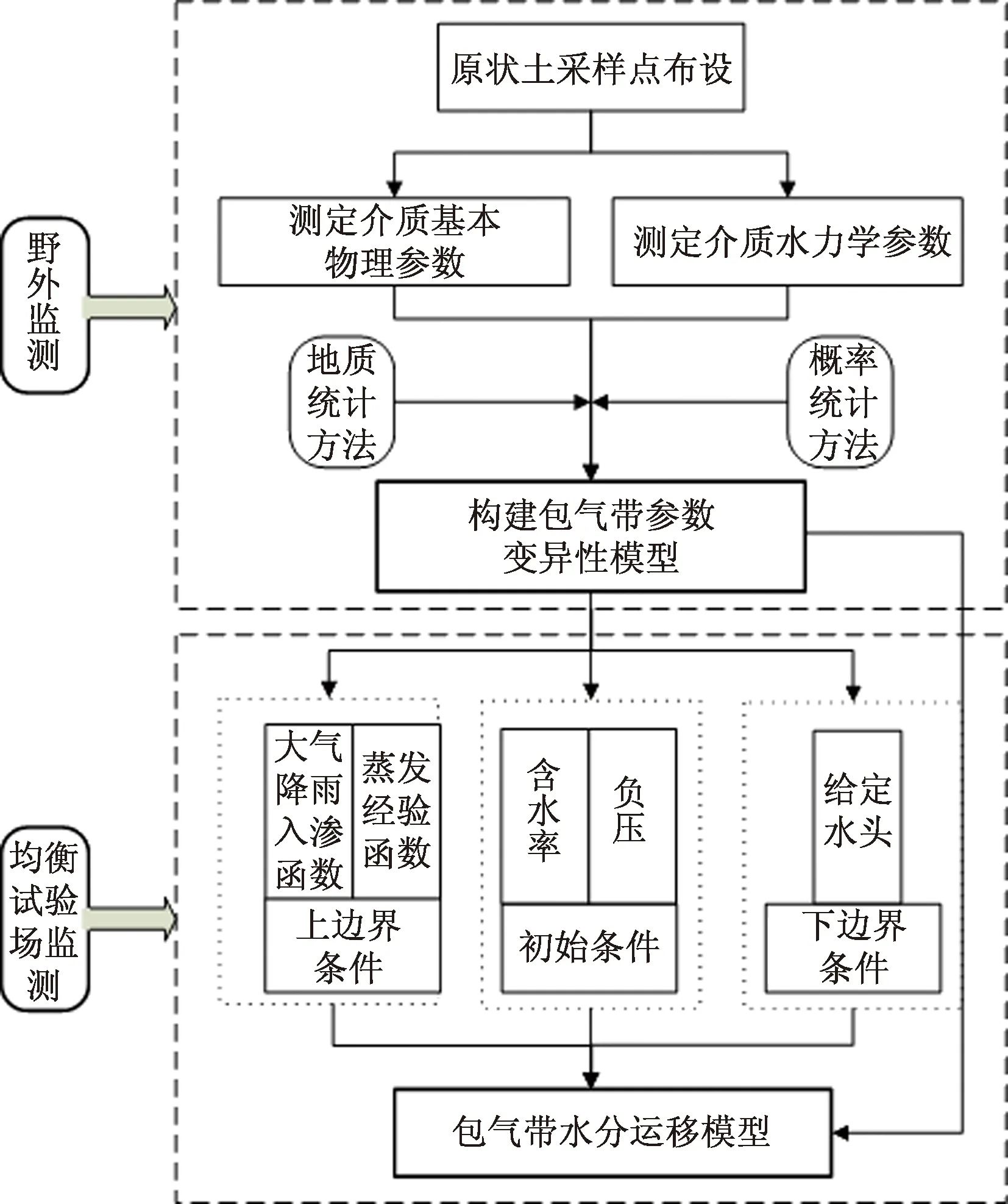
图2 野外监测与均衡试验场监测集成流程图Fig.2 Flow chart of integration of field monitoring and balanced experiment site monitoring
包气带参数变异性研究方法主要有传统的统计方法、时间序列分析方法、地统计学方法、随机模拟方法、分数维方法以及GIS的空间变异分析方法[18]。地统计学方法由于它注重变量因子的空间过程,考虑其空间分布特征和空间自相关而得到广泛应用[19]。它是通过变异函数可以确定和比较变量因子的空间变异程度及空间变异尺度, 以提供地理学、生态学和土壤学对自然现象及过程的空间变异特征解释。目前将地统计学方法和GIS 结合起来,一方面利用GIS 的空间分析功能,利用计算机的先进技术方便地实现地统计学的计算内插和制图要求;另一方面能够很好地描述因子的空间结构特征及其时间变化规律,是分析土壤水分空间特征及其变异规律最为有效的方法之一[17,20-22]。
3.1 包气带参数的概率模型
用经典统计学的基本理论,对不同位置、深度土壤含水量、干容重、颗分(黏粒和粉粒组成)、饱和渗透系数、孔隙率以及含水率、负压等参数统计其特征值。例如均值、中值、最大值、最小值、极差、标准差、离散系数。当离散系数Cv≤0.1为弱变异性, 0.1 现以干容重(λ;g/cm3)为例分析其统计分布特征。同一岩性在不同位置(平面与剖面)所取样品干容重最大值、最小值不同。并且这种变化是随机的,可依据统计方法获得均方差(σ)与数学期望(α)。将干容重视为随机变量δ,若 p(α-σ<δ<α+σ)=0.68 (1) p(α-2σ<δ<α+2σ)=0.956 (2) p(α-3σ<δ<α+3σ)=0.997 (3) 就认为干容重γ服从正态分布。 同理,对于包气带介质颗粒分析的不均匀系数(Cu)或曲率系数(Cc)、饱和渗透系数(K)及给水度(μ)的变异性都可以如此分析。 但是含水率与负压之间为函数关系,不能用上述分析方法,表述二者关系称为土壤水分特征曲线。目前统计模型有Van Geunchten模型、Brooks-Corey模型、Gardner-Russo模型、Campbell模型、Williams模型、Mckee和Bumb模型、Frdlund和Xing模型、Broadbridge-White模型、Burdine模型、Mualem模型等十余种[23],以Van Geunchten模型为例,土壤含水率与负压经验方程: θ=θγ+(θS-θγ)[(1+α|h|)n]-m m=1-1/n (4) 其中,α、n和m为统计经验参数;θs、θr、αw和nw为拟合吸湿过程参数;θs、θr、αd和nd为拟合脱湿过程参数;θs为饱和含水率;θr为残留含水率。 郑州地下水均衡试验场的岩性概化为:细砂、粉细砂、粉质黏土、粉土、黄土状粉土、黄土状粉质黏土夹粉质黏土、黏土7大类13种。经过一年以上含水率、负压监测就可以获得13种岩性建立脱湿与吸湿两种状态下的水分特征曲线模型。 渗透系数与负压关系的Van Geunchten经验方程为: (5) 式中:K(h)——渗透系数/ (m·d-1); Ks——饱和渗透系数/ (m·d-1),非饱和区则为压力水头的函数。 K(S)=KsS0.5[1-(1-S1/m)m]2 (6) 由式(4)~(6)可以看出,控制含水率或渗透系数经验方程都分别有1~2个独立待定常数。分析水分特征曲线的变异性本质是分析待定常数的变异性。 3.2.1合理选择场地取样数量 包气带参数变异性是一个随机问题,首要考虑样本容量的选择。如果取样点数目过少,所得结果缺乏代表性,甚至是错误的结论,但观测点数目过多,则需要消耗较多的人力、物力。用有限观测值去估计该参数的均值〈或期望)时,为保证足够的精度,取样或观测点的数目应合理确定[15]。若认为所采样品独立,而且取样容量足够,中心极限定理成立,可由置信区间满足取样数目合理性。 (7) 式中:Pl——置信水平,一般取值为95%; Δ——估值精度。 由中心极限定理随机变量为标准正态分布: (8) 结合式(7)、(8),可知取样点数目N为: N=3.84(σ/Δ)2 (9) 若取Δ=κμ,则可表述为: N=3.84(CV/k)2 (10) 当置信水平为95%,k=10%时,则取样数目对应于弱变异性,N<4 ,中等变异性,N=4~400,强变异性,N>400。 实际应用中,用样本方差代替总体方差,由统计学原理: (11) 其中,λα·f为t分布的特征值,可以查表得到,这样满足要求的取样数目即为: N=λ2α·f(S/Δ)2 (12) 根据式(12)可知,取样数目和所取置信水平及精度要求有关。 以河南省郑州地下水均衡试验场的推广应用为例,拟选择黄河南岸冲洪积平原某一试验场地为长9 km,宽6 km,布设网度为500 m,共计24 km2,117个采样点,见图3。试验场地在地下水位埋深7米内有7种岩性组合,预计一种岩性的采样容量大概是100,一个采样点不同深度采样5~7个,共计采样约600个。这个样本容量是区别于以往研究的特点之一,对于描述区域尺度包气带参数变异性的模型基本满足。 图3 原位采样点的布设Fig.3 Layout of in situ sampling points 此种原位采样点布置方案的特点是可组成500 m×500 m的网度,从而为获得包气带参数变异性模型与取样网度尺寸的关系提供借鉴。包气带样品为原状样,区别与以往扰动样,直径95 mm,高100 mm,拟选用取样效率较高的直推履带式取样钻(Geoprobe,6620DT)取样。并采用自行研制测量原状样的渗透系数与孔隙率及水分特征曲线测试仪器进行测试。 3.2.2包气带参数空间分布相关性的半方差分析 (13) 式中:N——所取测点的“对”数; (14) 表1 常用半方差函数拟合方程 3.2.3最优内插的Kriging法 在半方差分析的基础上,可以对未知点的参数值进行最优内插估计,即所谓的Kriging法。Kriging最优内插法利用了区域化变量的原始数据和半方差函数的结构性,对未知采样点的区域化变量的取值进行线性无偏最优估计,最终生成研究对象的空间分布。相比于一般线性内插方法,由于其方差较小,因而估值精度较高[16]。 目前在ArcGIS的Geostatistical Analyst模块采用kringing插值。需要注意的是标值前将特异性值剔除,才能避免插值结果偏离实际值,可以利用该模块的数据检查工具(ESDA)来完成。 获得野外包气带参数变异特征后,结合均衡试验场监测资料,构建降水入渗与蒸发条件下的数学模型: (15) 式中:θ——含水量/( cm3· cm-3); T——时间/d; h——压力水头/cm; K(θ)——非饱和渗透系数/(cm·h-1); R——植物根系吸水源汇项 /(cm3·cm-3·h-1); Z——垂直坐标轴,将坐标原点选在地面,向下设为正。 试验柱数学模型下边界取定水头边界(压力水头为零),用实测下边界流量进行校验。 试验柱上边界有三种状态:有压入渗、无压入渗和蒸发。有压和无压入渗可分别取变水头边界和流量边界;蒸发边界较复杂,下边界取定水头值,各类岩性水分特征曲线取实际测定值,以试验柱监测数据为基础,用数值模型方法反求上界蒸发强度EvtTop,结合表层(如5 cm) 实测平均含水率值θTop(或饱和度STOP),统计表层经验蒸发规律函数EvtTop(θTop),作为上部非线性通量边界条件: EvtTop(θTop)=Evt0f((θTop-θγ)/(θs-θγ))= Evt0f(STOP) STOP=(θTop-θγ)/(θs-θγ) (16) 式中:EvtTop——试验柱表层(如5 cm)日均蒸发强度/(cm·h-1); θTop——实验柱表层日均含水率/(cm3·cm-3); STOP——试验柱表层日均饱和度; Evt0——气象观测日均蒸发强度/(cm·h-1)。 试验柱初始条件根据所测的土壤含水量或负压确定。 另外,当试验柱数学模型建立之后,可在试验柱上边界处置不同溶质浓度,探讨在降水与蒸发条件下的溶质运移特征,并建立包气带水分、热量、溶质运移耦合模型,为土壤面状污染预测提供信息。 黄河南冲洪积区野外试验场地推广应用实践,可为黄河北冲洪积区、淮河冲积平原、南阳盆地、豫西黄土丘陵区潜水面蒸发与入渗补给的现场模拟提供示范作用,对于探讨黄河冲积平原降雨入渗补给或潜水蒸发特征,评价区域地下水资源的开发潜力提供一定的科学依据。

3.2 区域尺度包气带参数变异地学统计模型


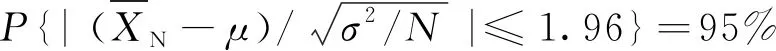


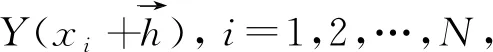
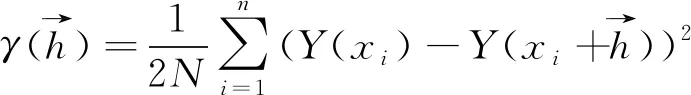


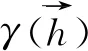


4 区域潜水面入渗或蒸发量估算


