基于自适应Hata模型的无线电发射源定位方法

史肖冰, 郭德贵, 曹 捷

(吉林大学 计算机科学与技术学院, 长春 130012)

随着移动通信的迅速发展, 频谱资源变得弥足珍贵, 使有效管理区域内频谱资源成为频谱管理部门的重要工作, 而定位无线电发射源是解决该问题的关键.目前无线电发射源定位的常用方法主要分为两步: 1)获得附近基站的某些参数, 例如电磁波的到达角度或到达时间; 2)通过这些参数定位无线电发射源[1], 例如到达时间(time of arrival, TOA)定位、 到达时间差(time difference of arrival, TDOA)定位、 到达角度(angle of arrival, AOA)定位等方法[2-6].这些方法都需要对多个站点安装昂贵的测向设备, 且对于参数值的精度要求很高, 定位无线电发射源的成本较高.在模型上, 目前的主要方法是根据传统模型计算功率值, 例如Okumura-Hata模型、 COST 231-Walfisch-Ikegami模型、 Okumura-Egli模型等[7-9], 得到的功率值固定.

本文在拥有大数据量的前提下, 提出利用大数据构造自适应Hata模型, 对模拟发射点利用自适应Hata模型求已知坐标点的功率值, 再与真实功率值做差, 得到误差值后, 选取误差最小的模拟发射点作为最优解.在求取最优解方面, 由于数据量较大, 直接求解困难, 因此本文采用粒子群优化算法, 可在不降低精确度的条件下更快地求得最优解.实验结果表明, 本文提出的基于自适应Hata模型的无线电发射源定位方法不会产生固定基站及测向设备的代价, 可有效地定位无线电发射源.

1 自适应Hata模型

Okumura-Hata模型[8]是一种广泛使用的传播模型, 适用于宏蜂窝(小区半径大于1 km)系统的路径损耗预测.由于本文测试数据在市区内获得, 所以采用针对市区的Hata模型, Hata模型的经验公式为

PL=69.55+26.16fc+13.82lghb-α(hm)+(44.9-6.55lghb)lgd,

(1)

其中:PL为市区路径平均损耗, 本文假设包含视距损耗和非视距损耗；fc为载波频率；hb为基站天线有效高度；α(hm)为移动天线的校正因子；d为移动台与基站之间的距离.发射功率和接收功率的关系为

Pr=Pt-PL,

(2)

其中:Pr为接收功率值；Pt为发射功率值.根据式(1)和式(2)可得：

Pr=Pt-69.55-26.16fc-13.82lghb+α(hm)-(44.9-6.55lghb)lgd.

(3)

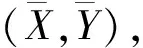
(4)

其中:

K=Pt-69.55-26.16fc-13.82lghb+α(hm);k=44.9-6.55lghb.

这两个值都是针对模拟发射源自适应变化的, 可更好地反应当前环境的参数.

(5)

通过联立方程可求得K和k, 分别为

(6)

(7)

在选取模拟发射源过程中, 由于是在某个特定范围区域内选取模拟发射源, 数据量庞大.粒子群优化算法适用于解决大数据求解问题, 所以本文采用粒子群优化算法选取模拟发射源.

由于最大功率点附近的点干扰较小, 计算得到的模型更准确, 所以选取接收功率最大值附近的10组点, 每组点包括两个实际接收点, 对每组点可求得一组K和k, 最后对10组K和k求平均值, 得到K和k, 即得到了改进的Hata模型.由于选取的模拟发射点不同, 得到的K和k也会出现差异, 所以在进行粒子群定位算法过程中, 每次构造的模型为自适应Hata模型.

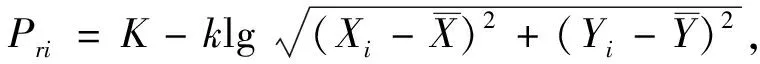
由于自适应Hata模型是根据最大功率值附近的接收点构造, 这些点受环境的干扰较小, 利用自适应Hata模型求最小E值, 该E值对应的模拟发射源即为要定位的真实发射源.

2 粒子群定位算法

粒子群优化算法[10]因其概念简明、 实现方便、 收敛速度快而被广泛应用.本文方法在求取最优模拟发射源时, 数据量较大, 直接求解较困难, 所以在实现定位算法时采用粒子群优化算法.实验结果表明, 粒子群优化算法可在不降低定位精度的条件下更快地定位发射源.

设每个粒子对应模拟发射点, 最终求得的最优粒子即为最优模拟发射点.本文的粒子群定位算法步骤如下:

1)初始化粒子群, 每个粒子的信息包括粒子坐标、 粒子速度、 粒子适应度和最优粒子的适应度;

2)初始化每个粒子, 粒子坐标为定位范围内的随机值, 粒子速度为0～1内的随机值, 粒子适应度为+∞, 初始化最优粒子, 与正常粒子初始化相同;

3)迭代更新粒子群;

4)遍历每个粒子, 设当前粒子为par, 更新par;

5)par根据坐标和速度更新坐标;

6)加速因子设为0～1的随机值, 根据加速因子和par与最优粒子的距离更新par的粒子速度;

7)利用ComputedFit算法更新par的粒子适应度；

8)比较par的粒子适应度与par的最优适应度, 如果比最优适应度小, 则更新par的最优适应度；

9)比较par的最优适应度与最优粒子的适应度, 如果比最优粒子的适应度小, 则更新最优粒子的适应度;

10)未达到最大迭代次数, 则转步骤4);

11)返回最优粒子.

其中ComputedFit算法表示对每个粒子求适应度, 是求模拟发射源与真实发射源的误差E的过程.计算步骤如下:

1)接收到的参数为一个粒子, 设为par;

2)判断par的经纬度是否超出实测范围, 若超出, 则返回∞; 否则转步骤3);

3)获得最大功率值接收点附近的20个接收点序列, 设为maxlist, 每个接收点包括功率值和坐标值;

4)根据maxlist可分成10组点, 每组包括2个接收点;

5)每组点根据式(6)可求得的值设为K;

6)每组点根据式(7)可求得的值设为k;

7)对10组K值求平均值, 设为K_m, 对10组k值求平均值, 设为k_m;

8)遍历每个真实接收点, 当前真实接收点设为par_real;

9)利用par的坐标、 par_real的坐标以及K_m和k_m, 由式(4)可求得预测值, 设为Pr；

10)对Pr和par_real的真实功率值(设为Ps)做差平方得到par_real的误差值;

11)对每个真实接收点都可以求得一个误差值;

12)最后求得误差值之和为适应度, 返回适应度.

3 实验与分析

图1 测试数据路线

本文采用的数据为车载监测设备在吉林省长春市内某区域行驶过程接收到的实际功率值, 所有频率的数据量大小为1.09 GB, 实验过程中提取了若干组常用频率的数据.以92.7 MHz频率数据为例, 测试数据的路线如图1所示.

表1为利用本文方法对若干组常用频率数据定位的发射源与真实发射源的误差.由表1可见, 在东西相差8.83 km, 南北相差10.02 km的范围内, 定位的误差值均在0.4 km内, 最小误差值约可达0.11 km.由误差值可见, 本文方法是有效的, 且对比成本方面, 传统方法需建造多个固定基站和测向设备, 造价很高, 而本文方法只需要利用移动车辆在定位范围内使用接收功率值的设备行驶一圈即可, 表明本文方法较传统方法成本低, 更实用.

表1 若干组频率数据定位的发射源与真实发射源误差

综上所述, 本文提出了一种基于自适应Hata模型的无线电发射源定位方法.首先, 利用大数据改造传统Hata模型, 得到自适应Hata模型后再定位；其次, 定位过程中使用了粒子群优化算法, 可在不降低精确度的条件下更快地求解.实验结果表明, 该方法可有效定位发射源, 且节省了固定基站和测向设备的开销, 利用车载监测设备上传的数据即可计算无线电发射源的位置.